人教A版(2019)必修第二册10.1随机事件与概率同步练习(Word含答案解析)
文档属性
| 名称 | 人教A版(2019)必修第二册10.1随机事件与概率同步练习(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 563.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 19:13:58 | ||
图片预览




文档简介
人教A版(2019)必修第二册 10.1 随机事件与概率 同步练习
一、单选题
1.分别独立的扔一枚骰子和硬币,并记下骰子向上的点数和硬币朝上的面,则结果中含有“点或正面向上”的概率为( )
A. B. C. D.
2.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是
A. B. C. D.
3.10张奖券中有4张“中奖”奖券,甲乙两人先后参加抽奖活动,每人从中不放回抽取一张奖券,甲先抽,乙后抽,在甲中奖条件下,乙没有中奖的概率为( )
A. B. C. D.
4.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
5.有两个事件,事件抛掷一枚均匀的骰子,朝上的面点数为偶数;事件人中至少有人生日相同.下列说法正确的是( )
A.事件、都是随机事件 B.事件、都是必然事件
C.事件是随机事件,事件是必然事件 D.事件是必然事件,事件是随机事件
6.袋中装有1个白球和3个黑球,从中摸出2个球正好一白一黑的概率是( )
A. B. C. D.
7.已知消费者购买家用小电器有两种方式:网上购买和实体店购买.经工商局抽样调查发现,网上家用小电器合格率约为,而实体店里家用小电器的合格率约为,工商局12315电话接到关于家用小电器不合格的投诉,统计得知,被投诉的是在网上购买的概率约为.那么估计在网上购买家用小电器的人约占( )
A. B. C. D.
8.从装有完全相同的4个红球和2个黄球的盒子中任取2个小球,则互为对立事件的是
A.“至少一个红球”与“至少一个黄球” B.“至多一个红球”与“都是红球”
C.“都是红球”与“都是黄球” D.“至少一个红球”与“至多一个黄球”
9.已知某工厂生产的产品的合格率为90%现采用随机模拟的方法估计4件产品中至少有3件为合格品的概率:先由计算器产生0到9之间取整数值的随机数,指定0表示不是合格品,1,2,3,4,5,6,7,8,9表示是合格品;再以每4个随机数为一组,代表4件产品,经随机模拟产生了如下20组随机数:
7527 0293 7040 9857 0347 4373 8636 6947 1417 4698
0301 6233 2616 8045 6001 3661 9597 7424 7610 4001
掘此估计,4件产品中至少有3件合格品的概率为( )
A. B. C. D.
10.从装有两个白球和两个黄球的口袋中任取2个球,以下给出了四组事件:
①至少有1个白球与至少有1个黄球;
②至少有1个黄球与都是黄球;
③恰有1个白球与恰有1个黄球;
④恰有1个白球与都是黄球.
其中互斥而不对立的事件共有( )
A.0组 B.1组
C.2组 D.3组
11.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马劣于齐王的上等马,优于齐王的中等马,田忌的中等马劣于齐王的中等马,优于齐王的下等马,田忌的下等马劣于齐王的下等马,现两人进行赛马比赛,比赛规则为:每匹马只能用一次,每场比赛双方各出一匹马,共比赛三场.每场比赛中胜者得1分,否则得0分.若每场比赛之前彼此都不知道对方所用之马,则比赛结束时,田忌得2分的概率为( ).
A. B. C. D.
12.七巧板,又称七巧图、智慧板,是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,于明、清两代在民间广泛流传.某同学用边长为4 dm的正方形木板制作了一套七巧板,如图所示,包括5个等腰直角三角形,1个正方形和1个平行四边形.若该同学从5个三角形中任取出2个,则这2个三角形的面积之和不小于另外3个三角形面积之和的概率是( )
A. B. C. D.
二、填空题
13.在10个学生中,男生有x人.现从10个学生中任选6人去参加某项活动,有下列事件:
①至少有1个女生;②5个男生,1个女生;③3个男生,3个女生.
若要使①为必然事件,②为不可能事件,③为随机事件,则x为________.
14.某种商品共100件,其中一等品35件,二等品55件,其余为次品.某人购买一件该商品,则他买到一等品的概率为__________.
15.小华、小明、小李小章去A,B,C三个工厂参加社会实践,要求每个工厂都有人去,且这四人都在这三个工厂实践,则小华和小李都没去B工厂的概率是________.
16.某人将甲、乙两颗骰子先后各抛一次,a,b分别表示抛掷甲、乙两棵骰子所得的点数,若点落在不等式组表示的平面区域内的事件记为A,则事件A的概率是________.
17.古希腊哲学家毕达哥拉斯曾说过:“美的线型和其他一切美的形体都必须有对称形式”.在中华传统文化里,建筑、器物、书法、诗歌、对联、绘画几乎无不讲究对称之美.如清代诗人黄柏权的《茶壶回文诗》(如图)以连环诗的形式展现,20个字绕着茶壶成一圆环,不论顺着读还是逆着读,皆成佳作.数学与生活也有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,两位数的回文数共有9个(11,22,…,99),则在三位数的回文数中,出现偶数的概率为_____________.
三、解答题
18.起源于汉代的“踢键子”运动,虽有两千多年历史,但由于简便易行,至今仍很流行.某校为丰富课外活动、增强学生体质,在高一年级进行了“踢键子”比赛,以学生每分钟踢毯子的个数记录分值,一个记一分.参赛学生踢键子的分值均在分之间,从中随机抽取了100个样本学生踢键子的成绩进行统计分析,绘制了如图所示的频率分布直方图,并称得分在之间为“踢毽健将”,90分以上为“踢建达人”.
(1)求样本的平均值(同一组数据用该区间的中点值代替);
(2)要在“踢毽健将”和“踢建达人”中分层抽样抽出6名同学在全级进行表演,试问“踢毽达人”张睿被抽取的概率是多少?
(3)以样本的频率值为概率,若高一(1)班有60个同学,试估计该班“踢毽健将”和“踢健达人”各有多少人.
19.某校高二年级(1)(2)班准备联合举行晚会,组织者欲使晚会气氛热烈、有趣,策划整场晚会以转盘游戏的方式进行,每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.(1)班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时(1)班代表获胜,否则(2)班代表获胜.该方案对双方是否公平?为什么?
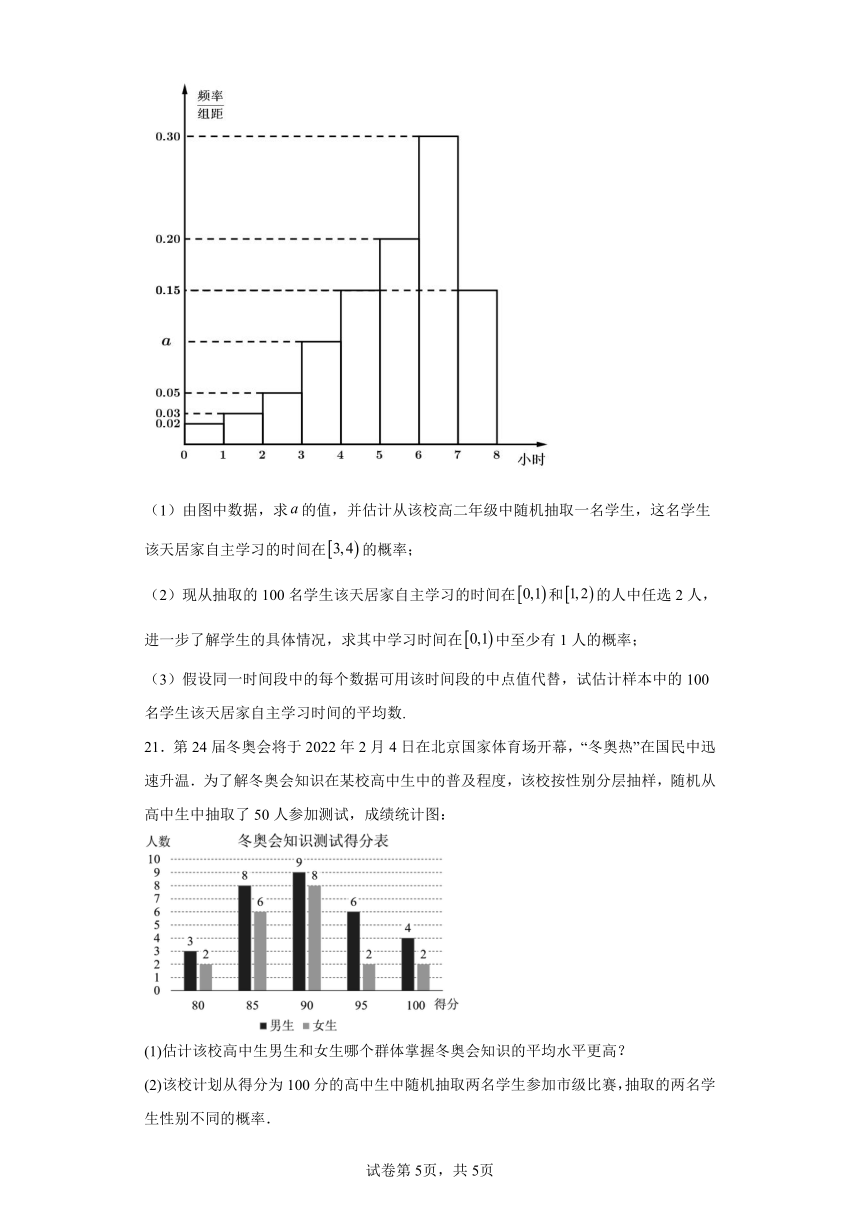
20.在新冠肺炎疫情期间,为了认真贯彻落实北京市教委关于做好中小学生延期开学期间“停课不停学”工作要求,各校以教师线上指导帮助和学生居家自主学习相结合的教学模式积极开展工作.为了解学生居家自主学习的情况,从某校高二年级随机抽取了100名学生,获得了他们一天中用于居家自主学习的时间分别在,,(单位:小时)的数据,整理得到的数据绘制成频率分布直方图(如图).
(1)由图中数据,求的值,并估计从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习的时间在的概率;
(2)现从抽取的100名学生该天居家自主学习的时间在和的人中任选2人,进一步了解学生的具体情况,求其中学习时间在中至少有1人的概率;
(3)假设同一时间段中的每个数据可用该时间段的中点值代替,试估计样本中的100名学生该天居家自主学习时间的平均数.
21.第24届冬奥会将于2022年2月4日在北京国家体育场开幕,“冬奥热”在国民中迅速升温.为了解冬奥会知识在某校高中生中的普及程度,该校按性别分层抽样,随机从高中生中抽取了50人参加测试,成绩统计图:
(1)估计该校高中生男生和女生哪个群体掌握冬奥会知识的平均水平更高?
(2)该校计划从得分为100分的高中生中随机抽取两名学生参加市级比赛,抽取的两名学生性别不同的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
列出所有的基本事件,再结果中含有“点或正面向上”的基本事件,利用古典概型的概率公式即可求得.
【详解】
分别独立的扔一枚骰子和硬币,所以的基本事件是:正面向上,反面向上,正面向上,反面向上,正面向上,反面向上,正面向上,反面向上,正面向上,反面向上,正面向上,反面向上.共个基本事件.
含有“点或正面向上”有正面向上,反面向上,正面向上,正面向上, 正面向上, 正面向上,正面向上,共个基本事件,
结果中含有“点或正面向上”的概率为:.
故选:.
本题主要考查的是随机事件概率的求解,古典概型的概率求解,利用列举法求解是解题的关键,是基础题.
2.D
男女生人数相同可利用整体发分析出两位女生相邻的概率,进而得解.
【详解】
两位男同学和两位女同学排成一列,因为男生和女生人数相等,两位女生相邻与不相邻的排法种数相同,所以两位女生相邻与不相邻的概率均是.故选D.
本题考查常见背景中的古典概型,渗透了数学建模和数学运算素养.采取等同法,利用等价转化的思想解题.
3.B
根据题意,分析甲先抽,并且中奖后剩余的奖券和“中奖”奖券的数目,由古典摡型的概率计算公式,即可求解.
【详解】
根据题意,10张奖券中有4张“中奖”奖券,甲先抽,并且中奖,
此时还有9张奖券,其中3张为“中奖”奖券,
则在甲中奖条件下,乙没有中奖的概率.
故选:B.
4.A
事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】
事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
5.C
判断事件、的类型,由此可得出结论.
【详解】
对于事件,抛掷一枚均匀的骰子,朝上的面的点数可能是奇数,也可能是偶数,则事件为随机事件;
对于事件B,一年有天或天,由抽屉原理可知,人中至少有人生日相同,事件为必然事件.
故选:C.
本题考查事件类型的判断,属于基础题.
6.A
设1个白球为A,3个黑球分别为,运用列举法列出基本事件,找出此事件中包含的基本事件数,再运用古典概率公式可得选项.
【详解】
设1个白球为A,3个黑球分别为,从中摸出2个球,有以下的情况:, ,,,,,基本事件总数为6 ,其中摸出2个球正好一白一黑的情况有:, ,,共有3种情况,所以摸出2个球正好一白一黑的概率为:,
故选:A.
本题考查古典概型概率的求法,运用列举法是常用的方法,属于基础题.
7.A
设在网上购买的人数占比为,实体店购买的人数占比为,分别求出各自被投诉的人数的占比,即可求解.
【详解】
设在网上购买的人数占比为,实体店购买的人数占比为,
由题意可得,网上购买的合格率为,
则网上购买被投诉的人数占比为,实体店里购买的被投诉的人数占比为,
所以,解得.
故选:A.
本题主要考查了概率的应用,其中解答中认真审题,求出各自被投诉的人数的占比是解答的关键,着重考查分析问题和解答问题的能力.
8.B
A选项“至少一个红球”与“至少一个黄球”可以同时发生;B选项说法正确;
C选项仅仅是互斥而不是对立;D选项“至少一个红球”与“至多一个黄球”可以同时发生.
【详解】
从装有完全相同的4个红球和2个黄球的盒子中任取2个小球,
各种情况为:两红,一红一黄,两黄,三种情况,
“至少一个红球”即一红一黄或两红,“至少一个黄球”即一红一黄或两黄,所以这两个事件不是对立事件;
“至多一个红球”即一黄一红或两黄,与“都是红球”互为对立事件;
“都是红球”与“都是黄球”仅仅是互斥事件;
“至少一个红球”即一红一黄或两红,“至多一个黄球”即一红一黄或两红,不是对立事件.
故选:B
此题考查对立事件的辨析,关键在于弄清每个选项中的事件的本质意义.
9.D
0表示不是合格品,4件产品中至多出现一次0,根据概率计算公式即可求解.
【详解】
4件产品中至多出现一次0,共个,
所以4件产品中至少有3件合格品的概率为.
故选:D
10.B
根据互斥事件和对立事件的定义,即可判断
【详解】
①中“至少有1个白球”与“至少有1个黄球”可以同时发生,如恰有1个白球和1个黄球,①中的两个事件不是互斥事件.
②中“至少有1个黄球”说明可以是1个白球和1个黄球或2个黄球,则两个事件不互斥.
③中“恰有1个白球”与“恰有1个黄球”,都是指有1个白球和1个黄球,因此两个事件是同一事件.
④中两事件不能同时发生,也可能都不发生,因此两事件是互斥事件,但不是对立事件;
故选:B.
11.C
根据题意,设齐王的上,中,下三个等次的马分别为a, b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,用列举法列举齐王与田忌赛马的情况,进而可得田忌胜出的情况数目,进而由等可能事件的概率计算可得答案.
【详解】
设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,双方各出上、中、下等马各1匹分组分别进行1场比赛,
所有的可能为:
Aa,Bb,Cc,田忌得0分;
Aa,Bc,Cb,田忌得1分
Ba,Ab,Cc,田忌得1分
Ba,Ac,Cb,田忌得1分;
Ca,Ab,Bc,田忌得2分,
Ca,Ac,Bb,田忌得1分
田忌得2分概率为,
故选:C
12.D
先逐个求解所有5个三角形的面积,再根据要求计算概率.
【详解】
如图所示,,,,,的面积分别为,,.
将,,,,分别记为,,,,,从这5个三角形中任取出2个,则样本空间,共有10个样本点.
记事件表示“从5个三角形中任取出2个,这2个三角形的面积之和不小于另外3个三角形面积之和”,则事件包含的样本点为,,,共3个,所以.
故选:D.
13.3或4.
根据必然事件、不可能事件还是随机事件的定义确定,“5个男生”为不可能事件,说明男生人数少于5,这里“至少有1个女生”为必然事件,不需要再考虑,但“3个男生,3个女生”为随机事件,则男生人数不能少于3,否则为不可能事件,由此可得的可能值.
【详解】
由题意知,10个学生中,男生人数少于5,但不少于3,所以或.
故答案为:3或4.
本题考查必然事件、不可能事件还是随机事件的定义,属于基础题.
14.##0.35
利用古典概型的概率计算公式即得.
【详解】
由题知某人购买一件该商品共包含基本事件100个,其中他买到一等品的基本事件有35个,
故他买到一等品的概率为.
故答案为:
15.
求出总的分配方法数,再按去1人或2人分类求得小华和小李都没去B工厂的方法数,然后由概率公式计算.
【详解】
由题意可知总的分配情况有种,其中满足条件的情况有种,故所求概率.
故答案为:.
16.
由抛掷两颗骰子有种不同结果.而点在不等式所表示的区域内,,运用列举法列出所有满足条件的点,再利用古典概率公式可求得答案..
【详解】
因抛掷一颗骰子有6种结果,所以抛掷两颗骰子有种不同结果.
点在不等式所表示的区域内,,有如下几种情况:
当时,,2,3;
当时,,2;当时,.
所以共有,,,,,六个点落在条件区域内,
故.
故答案为:.
17.
首先求出所有的三位数回文数的个数,再求出偶数的三位数回文数的个数,最后根据古典概型的概率公式求解即可.
【详解】
由题意可知,所有的三位数中回文数有:
,, 共90个,
其中偶数的回文数共有40个,
根据古典概型的概率公式得:,
故答案为:.
有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举.(2)注意区分排列与组合,以及计数原理的正确使用.
18.(1)68;
(2);
(3)“踢毽健将”人;“踢毽达人”人.
(1)写出频率分布直方图中各组数据的频率,再求平均数;
(2)由分层抽样求出抽出的6人中,“踢毽达人”应抽人数,再由古典概型求解;
(3)由“踢毽健将”和“踢毽达人”的频率,估计对应的概率,依据古典概型求得.
【详解】
(1)由,
样本的平均值为68;
(2)依频率分布直方图“踢毽健将”有10人,“踢毽达人”有5人.
需分层抽样抽6人,则要在“踢毽达人”中抽取2人,
所有的抽法共10种,包含张睿的抽法有4种,
故张睿同学被抽取的概率是.
(3)由频率分布直方图知,“踢毽健将”和“踢毽达人”的频率分别是0.1和0.05,
由此估计“踢毽健将”和“踢毽达人”的概率分别是0.1和0.05,
所以高一(1)班“踢毽健将”有人,“踢毽达人”有人.
19.该方案是公平的,理由见解析.
将各种情况利用表格,列出基本事件个数,再利用古典概型计算两数字之和为偶数或奇数的概率即可判断游戏是否公平.
【详解】
该方案是公平的,理由如下:
各种情况如表所示:
和 4 5 6 7
1 5 6 7 8
2 6 7 8 9
3 7 8 9 10
由表可知该游戏可能出现的情况共有12种,
其中两数字之和为偶数的有6种,为奇数的也有6种,
所以(1)班代表获胜的概率P1==,
(2)班代表获胜的概率P2==,即P1=P2,机会是均等的,
所以该方案对双方是公平的.
本题考查了古典概型的概率计算公式、写出基本事件个数,属于基础题.
20.(1);;(2);(3)5.38小时.
(1)由频率之和等于求出的值,这名学生该天居家自主学习的时间在的概率;
(2)由频率分布直方图可知自主学习时间在和的人分别有2人和3人,设在的2人分别为,在的3人分别,利用列举法结合古典概型的概率公式得出概率;
(3)由频率分布直方图中的数据,求解平均数即可.
【详解】
解:(1)因为,所以.
由图可得:随机抽取的100名学生中居家自主学习时间该天在的频率为
所以从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习时间在的概率为.
(2)设“抽取的2人其中学习时间在中至少有1人”为事件A
由图中数据可知:该天居家自主学习时间在和的人分别有2人和3人.
设在的2人分别为,在的3人分别
则从这5人中任选2人的样本空间,
共有10个,样本点事件A,
共有7个样本点
所以学习时间在中至少有1人的概率为
(3)样本平均数:
.
样本中的100名学生该天居家自主学习时间的平均数为5.38小时.
关键点睛:在第一问中,关键是利用频率之和等于求出的值,在第二问中主要是利用列举法求解概率.
21.(1)该校高中生男生群体掌握冬奥会知识的平均水平高于女生
(2)
(1)先求出男生和女生的平均分、,比较两个数的大小即可;
(2)设男生中满分学生分别为,,,,女生满分学生分别为A,,利用列举法列出所有可能的结果和性别不同的结果,进而得出答案.
(1)
设男生和女生的平均得分分别为、,则
,
.
∵,∴该校高中生男生群体掌握冬奥会知识的平均水平高于女生.
(2)
由统计图可知,得分为100分的人数为6人,
设男生中满分学生分别为,,,,女生满分学生分别为A,,共6人,现从6人中随机抽取两人,共有如下15种可能:
,,,,,
,,,,
,,,
,,
,
其中性别不同的有如下8种可能:
,;,;,;,.
∴抽取的两名学生性别不同的概率为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.分别独立的扔一枚骰子和硬币,并记下骰子向上的点数和硬币朝上的面,则结果中含有“点或正面向上”的概率为( )
A. B. C. D.
2.两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是
A. B. C. D.
3.10张奖券中有4张“中奖”奖券,甲乙两人先后参加抽奖活动,每人从中不放回抽取一张奖券,甲先抽,乙后抽,在甲中奖条件下,乙没有中奖的概率为( )
A. B. C. D.
4.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
5.有两个事件,事件抛掷一枚均匀的骰子,朝上的面点数为偶数;事件人中至少有人生日相同.下列说法正确的是( )
A.事件、都是随机事件 B.事件、都是必然事件
C.事件是随机事件,事件是必然事件 D.事件是必然事件,事件是随机事件
6.袋中装有1个白球和3个黑球,从中摸出2个球正好一白一黑的概率是( )
A. B. C. D.
7.已知消费者购买家用小电器有两种方式:网上购买和实体店购买.经工商局抽样调查发现,网上家用小电器合格率约为,而实体店里家用小电器的合格率约为,工商局12315电话接到关于家用小电器不合格的投诉,统计得知,被投诉的是在网上购买的概率约为.那么估计在网上购买家用小电器的人约占( )
A. B. C. D.
8.从装有完全相同的4个红球和2个黄球的盒子中任取2个小球,则互为对立事件的是
A.“至少一个红球”与“至少一个黄球” B.“至多一个红球”与“都是红球”
C.“都是红球”与“都是黄球” D.“至少一个红球”与“至多一个黄球”
9.已知某工厂生产的产品的合格率为90%现采用随机模拟的方法估计4件产品中至少有3件为合格品的概率:先由计算器产生0到9之间取整数值的随机数,指定0表示不是合格品,1,2,3,4,5,6,7,8,9表示是合格品;再以每4个随机数为一组,代表4件产品,经随机模拟产生了如下20组随机数:
7527 0293 7040 9857 0347 4373 8636 6947 1417 4698
0301 6233 2616 8045 6001 3661 9597 7424 7610 4001
掘此估计,4件产品中至少有3件合格品的概率为( )
A. B. C. D.
10.从装有两个白球和两个黄球的口袋中任取2个球,以下给出了四组事件:
①至少有1个白球与至少有1个黄球;
②至少有1个黄球与都是黄球;
③恰有1个白球与恰有1个黄球;
④恰有1个白球与都是黄球.
其中互斥而不对立的事件共有( )
A.0组 B.1组
C.2组 D.3组
11.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马劣于齐王的上等马,优于齐王的中等马,田忌的中等马劣于齐王的中等马,优于齐王的下等马,田忌的下等马劣于齐王的下等马,现两人进行赛马比赛,比赛规则为:每匹马只能用一次,每场比赛双方各出一匹马,共比赛三场.每场比赛中胜者得1分,否则得0分.若每场比赛之前彼此都不知道对方所用之马,则比赛结束时,田忌得2分的概率为( ).
A. B. C. D.
12.七巧板,又称七巧图、智慧板,是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,于明、清两代在民间广泛流传.某同学用边长为4 dm的正方形木板制作了一套七巧板,如图所示,包括5个等腰直角三角形,1个正方形和1个平行四边形.若该同学从5个三角形中任取出2个,则这2个三角形的面积之和不小于另外3个三角形面积之和的概率是( )
A. B. C. D.
二、填空题
13.在10个学生中,男生有x人.现从10个学生中任选6人去参加某项活动,有下列事件:
①至少有1个女生;②5个男生,1个女生;③3个男生,3个女生.
若要使①为必然事件,②为不可能事件,③为随机事件,则x为________.
14.某种商品共100件,其中一等品35件,二等品55件,其余为次品.某人购买一件该商品,则他买到一等品的概率为__________.
15.小华、小明、小李小章去A,B,C三个工厂参加社会实践,要求每个工厂都有人去,且这四人都在这三个工厂实践,则小华和小李都没去B工厂的概率是________.
16.某人将甲、乙两颗骰子先后各抛一次,a,b分别表示抛掷甲、乙两棵骰子所得的点数,若点落在不等式组表示的平面区域内的事件记为A,则事件A的概率是________.
17.古希腊哲学家毕达哥拉斯曾说过:“美的线型和其他一切美的形体都必须有对称形式”.在中华传统文化里,建筑、器物、书法、诗歌、对联、绘画几乎无不讲究对称之美.如清代诗人黄柏权的《茶壶回文诗》(如图)以连环诗的形式展现,20个字绕着茶壶成一圆环,不论顺着读还是逆着读,皆成佳作.数学与生活也有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,两位数的回文数共有9个(11,22,…,99),则在三位数的回文数中,出现偶数的概率为_____________.
三、解答题
18.起源于汉代的“踢键子”运动,虽有两千多年历史,但由于简便易行,至今仍很流行.某校为丰富课外活动、增强学生体质,在高一年级进行了“踢键子”比赛,以学生每分钟踢毯子的个数记录分值,一个记一分.参赛学生踢键子的分值均在分之间,从中随机抽取了100个样本学生踢键子的成绩进行统计分析,绘制了如图所示的频率分布直方图,并称得分在之间为“踢毽健将”,90分以上为“踢建达人”.
(1)求样本的平均值(同一组数据用该区间的中点值代替);
(2)要在“踢毽健将”和“踢建达人”中分层抽样抽出6名同学在全级进行表演,试问“踢毽达人”张睿被抽取的概率是多少?
(3)以样本的频率值为概率,若高一(1)班有60个同学,试估计该班“踢毽健将”和“踢健达人”各有多少人.
19.某校高二年级(1)(2)班准备联合举行晚会,组织者欲使晚会气氛热烈、有趣,策划整场晚会以转盘游戏的方式进行,每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.(1)班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时(1)班代表获胜,否则(2)班代表获胜.该方案对双方是否公平?为什么?
20.在新冠肺炎疫情期间,为了认真贯彻落实北京市教委关于做好中小学生延期开学期间“停课不停学”工作要求,各校以教师线上指导帮助和学生居家自主学习相结合的教学模式积极开展工作.为了解学生居家自主学习的情况,从某校高二年级随机抽取了100名学生,获得了他们一天中用于居家自主学习的时间分别在,,(单位:小时)的数据,整理得到的数据绘制成频率分布直方图(如图).
(1)由图中数据,求的值,并估计从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习的时间在的概率;
(2)现从抽取的100名学生该天居家自主学习的时间在和的人中任选2人,进一步了解学生的具体情况,求其中学习时间在中至少有1人的概率;
(3)假设同一时间段中的每个数据可用该时间段的中点值代替,试估计样本中的100名学生该天居家自主学习时间的平均数.
21.第24届冬奥会将于2022年2月4日在北京国家体育场开幕,“冬奥热”在国民中迅速升温.为了解冬奥会知识在某校高中生中的普及程度,该校按性别分层抽样,随机从高中生中抽取了50人参加测试,成绩统计图:
(1)估计该校高中生男生和女生哪个群体掌握冬奥会知识的平均水平更高?
(2)该校计划从得分为100分的高中生中随机抽取两名学生参加市级比赛,抽取的两名学生性别不同的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
列出所有的基本事件,再结果中含有“点或正面向上”的基本事件,利用古典概型的概率公式即可求得.
【详解】
分别独立的扔一枚骰子和硬币,所以的基本事件是:正面向上,反面向上,正面向上,反面向上,正面向上,反面向上,正面向上,反面向上,正面向上,反面向上,正面向上,反面向上.共个基本事件.
含有“点或正面向上”有正面向上,反面向上,正面向上,正面向上, 正面向上, 正面向上,正面向上,共个基本事件,
结果中含有“点或正面向上”的概率为:.
故选:.
本题主要考查的是随机事件概率的求解,古典概型的概率求解,利用列举法求解是解题的关键,是基础题.
2.D
男女生人数相同可利用整体发分析出两位女生相邻的概率,进而得解.
【详解】
两位男同学和两位女同学排成一列,因为男生和女生人数相等,两位女生相邻与不相邻的排法种数相同,所以两位女生相邻与不相邻的概率均是.故选D.
本题考查常见背景中的古典概型,渗透了数学建模和数学运算素养.采取等同法,利用等价转化的思想解题.
3.B
根据题意,分析甲先抽,并且中奖后剩余的奖券和“中奖”奖券的数目,由古典摡型的概率计算公式,即可求解.
【详解】
根据题意,10张奖券中有4张“中奖”奖券,甲先抽,并且中奖,
此时还有9张奖券,其中3张为“中奖”奖券,
则在甲中奖条件下,乙没有中奖的概率.
故选:B.
4.A
事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】
事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
5.C
判断事件、的类型,由此可得出结论.
【详解】
对于事件,抛掷一枚均匀的骰子,朝上的面的点数可能是奇数,也可能是偶数,则事件为随机事件;
对于事件B,一年有天或天,由抽屉原理可知,人中至少有人生日相同,事件为必然事件.
故选:C.
本题考查事件类型的判断,属于基础题.
6.A
设1个白球为A,3个黑球分别为,运用列举法列出基本事件,找出此事件中包含的基本事件数,再运用古典概率公式可得选项.
【详解】
设1个白球为A,3个黑球分别为,从中摸出2个球,有以下的情况:, ,,,,,基本事件总数为6 ,其中摸出2个球正好一白一黑的情况有:, ,,共有3种情况,所以摸出2个球正好一白一黑的概率为:,
故选:A.
本题考查古典概型概率的求法,运用列举法是常用的方法,属于基础题.
7.A
设在网上购买的人数占比为,实体店购买的人数占比为,分别求出各自被投诉的人数的占比,即可求解.
【详解】
设在网上购买的人数占比为,实体店购买的人数占比为,
由题意可得,网上购买的合格率为,
则网上购买被投诉的人数占比为,实体店里购买的被投诉的人数占比为,
所以,解得.
故选:A.
本题主要考查了概率的应用,其中解答中认真审题,求出各自被投诉的人数的占比是解答的关键,着重考查分析问题和解答问题的能力.
8.B
A选项“至少一个红球”与“至少一个黄球”可以同时发生;B选项说法正确;
C选项仅仅是互斥而不是对立;D选项“至少一个红球”与“至多一个黄球”可以同时发生.
【详解】
从装有完全相同的4个红球和2个黄球的盒子中任取2个小球,
各种情况为:两红,一红一黄,两黄,三种情况,
“至少一个红球”即一红一黄或两红,“至少一个黄球”即一红一黄或两黄,所以这两个事件不是对立事件;
“至多一个红球”即一黄一红或两黄,与“都是红球”互为对立事件;
“都是红球”与“都是黄球”仅仅是互斥事件;
“至少一个红球”即一红一黄或两红,“至多一个黄球”即一红一黄或两红,不是对立事件.
故选:B
此题考查对立事件的辨析,关键在于弄清每个选项中的事件的本质意义.
9.D
0表示不是合格品,4件产品中至多出现一次0,根据概率计算公式即可求解.
【详解】
4件产品中至多出现一次0,共个,
所以4件产品中至少有3件合格品的概率为.
故选:D
10.B
根据互斥事件和对立事件的定义,即可判断
【详解】
①中“至少有1个白球”与“至少有1个黄球”可以同时发生,如恰有1个白球和1个黄球,①中的两个事件不是互斥事件.
②中“至少有1个黄球”说明可以是1个白球和1个黄球或2个黄球,则两个事件不互斥.
③中“恰有1个白球”与“恰有1个黄球”,都是指有1个白球和1个黄球,因此两个事件是同一事件.
④中两事件不能同时发生,也可能都不发生,因此两事件是互斥事件,但不是对立事件;
故选:B.
11.C
根据题意,设齐王的上,中,下三个等次的马分别为a, b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,用列举法列举齐王与田忌赛马的情况,进而可得田忌胜出的情况数目,进而由等可能事件的概率计算可得答案.
【详解】
设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,双方各出上、中、下等马各1匹分组分别进行1场比赛,
所有的可能为:
Aa,Bb,Cc,田忌得0分;
Aa,Bc,Cb,田忌得1分
Ba,Ab,Cc,田忌得1分
Ba,Ac,Cb,田忌得1分;
Ca,Ab,Bc,田忌得2分,
Ca,Ac,Bb,田忌得1分
田忌得2分概率为,
故选:C
12.D
先逐个求解所有5个三角形的面积,再根据要求计算概率.
【详解】
如图所示,,,,,的面积分别为,,.
将,,,,分别记为,,,,,从这5个三角形中任取出2个,则样本空间,共有10个样本点.
记事件表示“从5个三角形中任取出2个,这2个三角形的面积之和不小于另外3个三角形面积之和”,则事件包含的样本点为,,,共3个,所以.
故选:D.
13.3或4.
根据必然事件、不可能事件还是随机事件的定义确定,“5个男生”为不可能事件,说明男生人数少于5,这里“至少有1个女生”为必然事件,不需要再考虑,但“3个男生,3个女生”为随机事件,则男生人数不能少于3,否则为不可能事件,由此可得的可能值.
【详解】
由题意知,10个学生中,男生人数少于5,但不少于3,所以或.
故答案为:3或4.
本题考查必然事件、不可能事件还是随机事件的定义,属于基础题.
14.##0.35
利用古典概型的概率计算公式即得.
【详解】
由题知某人购买一件该商品共包含基本事件100个,其中他买到一等品的基本事件有35个,
故他买到一等品的概率为.
故答案为:
15.
求出总的分配方法数,再按去1人或2人分类求得小华和小李都没去B工厂的方法数,然后由概率公式计算.
【详解】
由题意可知总的分配情况有种,其中满足条件的情况有种,故所求概率.
故答案为:.
16.
由抛掷两颗骰子有种不同结果.而点在不等式所表示的区域内,,运用列举法列出所有满足条件的点,再利用古典概率公式可求得答案..
【详解】
因抛掷一颗骰子有6种结果,所以抛掷两颗骰子有种不同结果.
点在不等式所表示的区域内,,有如下几种情况:
当时,,2,3;
当时,,2;当时,.
所以共有,,,,,六个点落在条件区域内,
故.
故答案为:.
17.
首先求出所有的三位数回文数的个数,再求出偶数的三位数回文数的个数,最后根据古典概型的概率公式求解即可.
【详解】
由题意可知,所有的三位数中回文数有:
,, 共90个,
其中偶数的回文数共有40个,
根据古典概型的概率公式得:,
故答案为:.
有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举.(2)注意区分排列与组合,以及计数原理的正确使用.
18.(1)68;
(2);
(3)“踢毽健将”人;“踢毽达人”人.
(1)写出频率分布直方图中各组数据的频率,再求平均数;
(2)由分层抽样求出抽出的6人中,“踢毽达人”应抽人数,再由古典概型求解;
(3)由“踢毽健将”和“踢毽达人”的频率,估计对应的概率,依据古典概型求得.
【详解】
(1)由,
样本的平均值为68;
(2)依频率分布直方图“踢毽健将”有10人,“踢毽达人”有5人.
需分层抽样抽6人,则要在“踢毽达人”中抽取2人,
所有的抽法共10种,包含张睿的抽法有4种,
故张睿同学被抽取的概率是.
(3)由频率分布直方图知,“踢毽健将”和“踢毽达人”的频率分别是0.1和0.05,
由此估计“踢毽健将”和“踢毽达人”的概率分别是0.1和0.05,
所以高一(1)班“踢毽健将”有人,“踢毽达人”有人.
19.该方案是公平的,理由见解析.
将各种情况利用表格,列出基本事件个数,再利用古典概型计算两数字之和为偶数或奇数的概率即可判断游戏是否公平.
【详解】
该方案是公平的,理由如下:
各种情况如表所示:
和 4 5 6 7
1 5 6 7 8
2 6 7 8 9
3 7 8 9 10
由表可知该游戏可能出现的情况共有12种,
其中两数字之和为偶数的有6种,为奇数的也有6种,
所以(1)班代表获胜的概率P1==,
(2)班代表获胜的概率P2==,即P1=P2,机会是均等的,
所以该方案对双方是公平的.
本题考查了古典概型的概率计算公式、写出基本事件个数,属于基础题.
20.(1);;(2);(3)5.38小时.
(1)由频率之和等于求出的值,这名学生该天居家自主学习的时间在的概率;
(2)由频率分布直方图可知自主学习时间在和的人分别有2人和3人,设在的2人分别为,在的3人分别,利用列举法结合古典概型的概率公式得出概率;
(3)由频率分布直方图中的数据,求解平均数即可.
【详解】
解:(1)因为,所以.
由图可得:随机抽取的100名学生中居家自主学习时间该天在的频率为
所以从该校高二年级中随机抽取一名学生,这名学生该天居家自主学习时间在的概率为.
(2)设“抽取的2人其中学习时间在中至少有1人”为事件A
由图中数据可知:该天居家自主学习时间在和的人分别有2人和3人.
设在的2人分别为,在的3人分别
则从这5人中任选2人的样本空间,
共有10个,样本点事件A,
共有7个样本点
所以学习时间在中至少有1人的概率为
(3)样本平均数:
.
样本中的100名学生该天居家自主学习时间的平均数为5.38小时.
关键点睛:在第一问中,关键是利用频率之和等于求出的值,在第二问中主要是利用列举法求解概率.
21.(1)该校高中生男生群体掌握冬奥会知识的平均水平高于女生
(2)
(1)先求出男生和女生的平均分、,比较两个数的大小即可;
(2)设男生中满分学生分别为,,,,女生满分学生分别为A,,利用列举法列出所有可能的结果和性别不同的结果,进而得出答案.
(1)
设男生和女生的平均得分分别为、,则
,
.
∵,∴该校高中生男生群体掌握冬奥会知识的平均水平高于女生.
(2)
由统计图可知,得分为100分的人数为6人,
设男生中满分学生分别为,,,,女生满分学生分别为A,,共6人,现从6人中随机抽取两人,共有如下15种可能:
,,,,,
,,,,
,,,
,,
,
其中性别不同的有如下8种可能:
,;,;,;,.
∴抽取的两名学生性别不同的概率为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
