人教A版(2019)必修第二册第十章概率同步练习(Word含答案解析)
文档属性
| 名称 | 人教A版(2019)必修第二册第十章概率同步练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 439.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 19:22:34 | ||
图片预览




文档简介
人教A版(2019)必修第二册 第十章 概率 同步练习
一、单选题
1.一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,则摸出白球个数多于黑球个数的概率为( )
A. B. C. D.
2.某同学从家到学校要经过三个十字路口,设各路口信号灯工作相互独立,该同学在各路口遇到红灯的概率分别为,,,则该同学从家到学校至少遇到一次红灯的概率为( )
A. B. C. D.
3.下列说法错误的是( )
A.随机事件的概率与频率是一样的
B.在试验中,某事件发生的频率的取值范围是
C.必然事件的概率是1
D.不可能事件的概率是0
4.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A. B. C. D.
5.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.某天,齐王与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜,则田忌获胜概率为( ).
A. B. C. D.
6.以下三个命题:
①对立事件也是互斥事件;
②一个班级有50人,男生与女生的比例为3:2,利用分层抽样的方法,每个男生被抽到的概率为,每个女生被抽到的概率为;
③若事件,,两两互斥,则.
其中正确命题的个数为( )
A.0 B.1 C.2 D.3
7.甲、乙两人投篮,投中的概率分别为0.6,0.7,若两人各投2次,则两人投中次数不等的概率是( )
A.0.6076 B.0.7516 C.0.3924 D.0.2484
8.已知100件产品中有5件次品,从这100件产品中任意取出3件,设表示事件“3件产品 全不是次品”,表示事件“3件产品全是次品”,表示事件“3件产品中至少有1件是 次品”,则下列结论正确的是( )
A.与互斥 B.与互斥但不对立
C.任意两个事件均互斥 D.与对立
9.对关于的一元二次方程,通过掷骰子确定其中的系数,第一次出现的数作为,第二次出现的数作为(一颗骰子有6个面,分别刻有1、2,3、4、5、6六个数,每次扰掷,各数出现的可能性相同),那么,这个方程有解的概率是( )
A. B. C. D.
10.下列事件A,B是独立事件的是( )
A.一枚硬币掷两次,A=“第一次为正面向上”,B=“第二次为反面向上”
B.袋中有两个白球和两个黑球,不放回地摸两球,A=“第一次摸到白球”,B=“第二次摸到白球”
C.掷一枚骰子,A=“出现点数为奇数”,B=“出现点数为偶数”
D.A=“人能活到20岁”,B=“人能活到50岁”
11.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
12.掷一枚骰子的试验中,出现各点的概率均为,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A+(表示事件B的对立事件)发生的概率为( )
A. B. C. D.
二、填空题
13.若同时掷两颗骰子,则出现两颗骰子的点数之和大于9的概率为________
14.甲 乙两名同学进行篮球投篮练习,甲同学一次投篮命中的概率为,乙同学一次投篮命中的概率为,假设两人投篮命中与否互不影响,则甲 乙两人各投篮一次,至少有一人命中的概率是___________.
15.某产品分甲、乙、丙三级,其中甲级属正品,乙、丙两级属次品.若生产中出现乙级产品的概率为0.03,出现丙级产品的概率为0.01,则对成品任意抽查一件抽得正品的概率为__________.
16.已知A,B是相互独立事件,且,,则________.
三、解答题
17.今年中国共产党迎来了建党100周年,为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀,某区组织了党史知识竞赛活动.在最后一轮晋级比实中,甲、乙、丙三所学校回答一道有关红色革命根据地建立时间的问题,已知甲校回答正确这道题的概率为,甲、丙两所学校都回答正确这道题的概率是,乙、丙两所学校都回答正确这道题的概率是.若各学校回答这道题是否正确是互不影响的.
(1)求乙、丙两所学校各自回答正确这道题的概率;
(2)求甲、乙、丙三所学校中不少于2所学校回答正确这道题的概率.
18.在2016珠海航展志愿服务开始前,团珠海市委调查了北京师范大学珠海分校某班50名志愿者参加志愿服务礼仪培训和赛会应急救援培训的情况,数据如下表:单位:人
参加志愿服务礼仪培训 未参加志愿服务礼仪培训
参加赛会应急救援培训 8 8
未参加赛会应急救援培训 4 30
(1)从该班随机选1名同学,求该同学至少参加上述一个培训的概率;
(2)在既参加志愿服务礼仪培训又参加赛会应急救援培训的8名同学中,有5名男同学A,A,A,A,A名女同学B,B,B现从这5名男同学和3名女同学中各随机选1人,求A被选中且B未被选中的概率.
19.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
交付金额(元) 支付方式 (0,1000] (1000,2000] 大于2000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
20.某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13s内(称为合格)的概率分别为,,.若对这三名短跑运动员的100跑的成绩进行一次检测,则求:
(Ⅰ)三人都合格的概率;
(Ⅱ)三人都不合格的概率;
(Ⅲ)出现几人合格的概率最大.
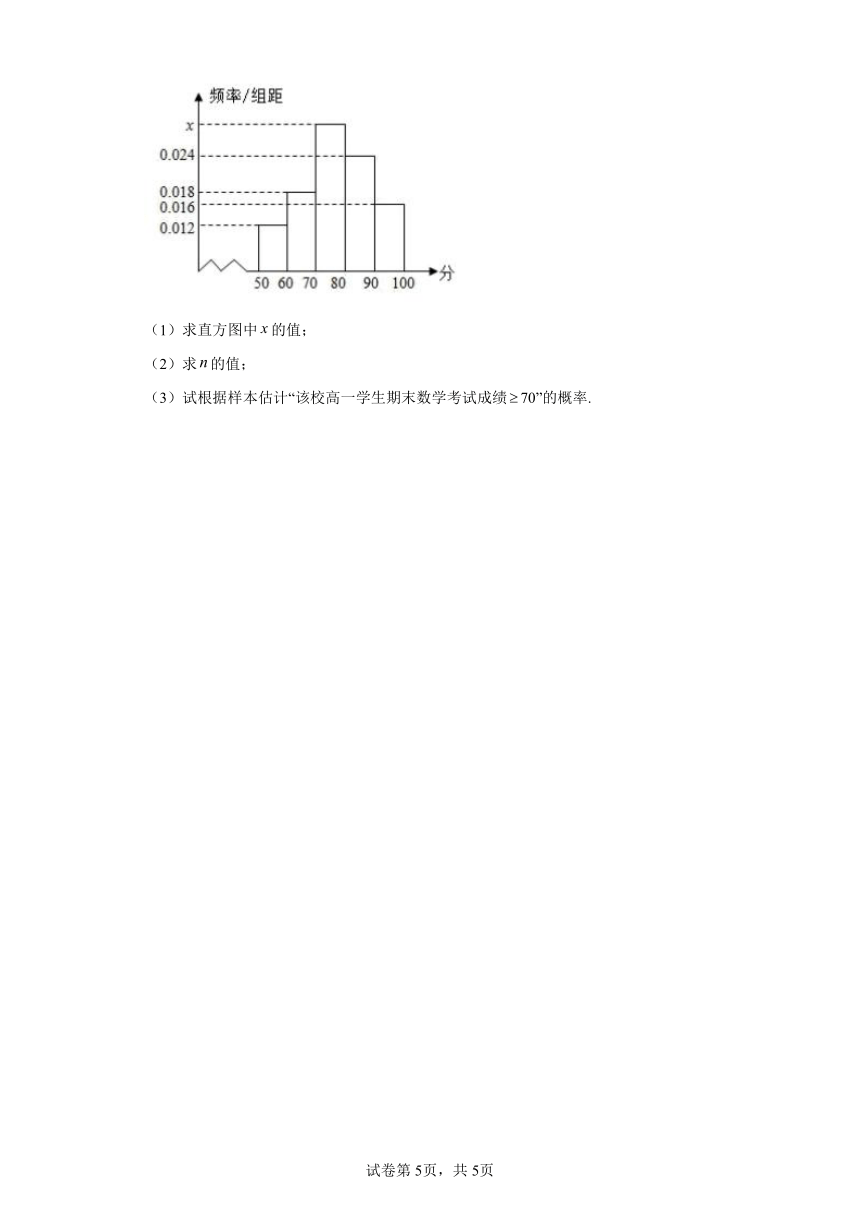
21.某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在的学生人数为6.
(1)求直方图中的值;
(2)求的值;
(3)试根据样本估计“该校高一学生期末数学考试成绩70”的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
根据古典概型的概念及计算公式直接计算即可.
【详解】
一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,
基本事件总数,
摸出白球个数多于黑球个数包含的基本事件个数,
则摸出白球个数多于黑球个数的概率为,
故选:C.
2.D
利用相互独立事件的概率乘法公式及对立事件的概率公式即可求解.
【详解】
解:由题意,该同学从家到学校至少遇到一次红灯的概率为,
故选:D.
3.A
依据频率和概率,必然事件和不可能事件的定义,依次判断即可
【详解】
对于选项A,概率是唯一的确定的值,而频率是统计出来的,通过一次次的试验得到,因此随机事件的概率与频率是两个不同的概念,故A错误;
对于选项B,频率是指是指每个对象出现的次数与总次数的比值,故取值范围是,故B正确;
对于选项C,D,由必然事件和不可能事件的定义可知,说法正确.
故选:A
4.D
根据题意,写出所有抽取的基本事件,再找出满足题意的基本事件,利用古典概型的概率计算公式即可求得结果.
【详解】
根据题意,不妨用表示两次抽取的基本事件,
其中代表第一次抽取的数字,代表第二次抽取的数字.
故所有抽取的可能有如下种:
满足抽得的第一张卡片上的数大于第二张卡片上的数的有如下种:
,
根据古典概型的概率计算公式可得:该事件的概率.
故选:D.
5.B
设齐王的三匹马分别为,田忌的三匹马分别为,列举所有比赛的情况,利用古典概型的概率公式计算即可得出结果.
【详解】
设齐王的三匹马分别为,田忌的三匹马分别为,所有比赛的情况::
、、,齐王获胜三局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,田忌获胜两局;
、、,齐王获胜两局,共6种情况,则田忌胜1种情况,故概率为
故选:B
本题考查了古典概型的概率计算问题,考查了理解辨析和数学运算能力,属于中档题目.
6.B
由对立事件的定义可判断①;由分层抽样的定义可判断②;由互斥事件的概率理解可判断③.
【详解】
对于①,由对立事件的定义可知对立事件一定是互斥事件,故①正确;
对应②,可知该班有男生30人,女生20人,由于不知道需要抽取多少人,所以无法得出概率,故②错误;
对应③,事件,,不一定包含所有事件,故,故③错误.
故选:B.
本题考查考查对事件互斥、对立的理解,考查对分层抽样的理解,属于基础题.
7.A
先求出两人投中次数相等的概率,再根据对立事件的概率公式可得两人投中次数不相等的概率.
【详解】
两人投中次数相等的概率P=,
故两人投中次数不相等的概率为:1﹣0.3924=0.6076.
故选:A.
本题考查了对立事件的概率公式和独立事件的概率公式,属于基础题.
8.D
列出基本事件,再结合互斥事件,对立事件的定义即可判断.
【详解】
设1表示取到正品, 0 表示取到次品,所有事件
则
故与不互斥,故A,C错
故与互斥且对立,故B错,D正确
故选:D
9.C
记事件 “方程有实根”.由,得:,利用列举法得到事件包含的基本事件的个数,又总的基本事件共个,由古典概型概率公式求出方程有解的概率.
【详解】
记事件 “方程有实根”.
由,得:
又基本事件共个,
其中事件包含19个基本事件,列举如下:
,,,,,,,,,,,,
,,,,,,,
所以,
故选:C.
10.A
利用相互独立事件的概念,对四个选项逐一分析排除,从而得出正确选项.
【详解】
对于A选项,两个事件发生,没有关系,故是相互独立事件.对于B选项,事件发生时,影响到事件,故不是相互独立事件.对于C选项,由于投的是一个骰子,是对立事件,所以不是相互独立事件.对于D选项,能活到岁的,可能也能活到岁,故不是相互独立事件.综上所述,本小题选A.
本小题主要考查相互独立事件的概念以及相互独立事件的识别,属于基础题.
11.A
事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】
事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
12.C
由题意知试验发生包含的所有事件共有6种,事件和事件是互斥事件,看出事件和事件包含的基本事件数,根据互斥事件和古典概型概率公式得到结果.
【详解】
解:事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:C.
13.
列举基本事件,直接套公式求概率.
【详解】
同时掷两颗骰子,有共36种情况;
而点数之和大于9包括共6种,
所以两颗骰子的点数之和大于9的概率为.
故答案为:.
14.
考虑两个人都不命中的概率,从而可求至少有一个人命中的概率.
【详解】
两个都不命中的概率为,
故至少有一人命中的概率是,
故答案为:.
15.0.96
根据题意,设抽取产品的等级分别为事件、、,且事件,,彼此互斥,根据概率事件加法公式,即可求解.
【详解】
记“抽出的产品为正品”为事件,“抽出的产品为乙级产品”为事件,“抽出的产品为丙级产品”为事件,则事件,,彼此互斥,且与是对立事件,所以.
故答案为:
本题考查对立事件概率公式,属于基础题.
16.
首先计算出事件和的概率,再根据相互独立事件同时发生的概率计算公式即可得结果.
【详解】
∵,,∴,.
又∵A,B是相互独立事件,∴和也为相互独立事件,
∴,
故答案为:.
本题主要考查相互独立事件的概率乘法公式,关键是理解“事件A与事件B相互独立”的意义,属于基础题.
17.(1)
(2)
(1)根据独立事件的概率公式计算;
(2)结合互斥事件、独立事件的概率公式计算.
(1)
设事件“甲学校回答正确这道题”,事件“乙学校回答正确这道题”,事件“丙学校回答正确这道题” ,
则,,,
∵各学校回答这道题是否正确是互不影响的.
∴事件A,B,C相互独立.
∴,
∴ ;
(2)
设事件“甲、乙、丙三所学校中不少于2所学校回答正确这道题”且两两互斥,
;
由于事件A,B,C相互独立.
所以
,
,
,
18.(1);(2).
(1)根据表中数据知未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,故至少参加上述一个培训的共有人.从而求得概率;
(2)从这5名男同学和3名女同学中各随机选1人,列出其一切可能的结果,从而求得被选中且未被选中的概率.
【详解】
解:由调查数据可知,既未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,
故至少参加上述一个培训的共有人.
从该班随机选1名同学,该同学至少参加上述一个培训的概率为;
从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的基本事件有:
,
,
,
共15个,
根据题意,这些基本事件的出现是等可能的,
事件“被选中且未被选中”所包含的基本事件有:,共2个,
被选中且未被选中的概率为.
19.(Ⅰ) ;
(Ⅱ)见解析;
(Ⅲ)见解析.
(Ⅰ)由题意利用古典概型计算公式可得满足题意的概率值;
(Ⅱ)首先确定X可能的取值,然后求得相应的概率值可得分布列,最后求解数学期望即可.
(Ⅲ)由题意结合概率的定义给出结论即可.
【详解】
(Ⅰ)由题意可知,两种支付方式都是用的人数为:人,则:
该学生上个月A,B两种支付方式都使用的概率.
(Ⅱ)由题意可知,
仅使用A支付方法的学生中,金额不大于1000的人数占,金额大于1000的人数占,
仅使用B支付方法的学生中,金额不大于1000的人数占,金额大于1000的人数占,
且X可能的取值为0,1,2.
,,,
X的分布列为:
X 0 1 2
其数学期望:.
(Ⅲ)我们不认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化.理由如下:
随机事件在一次随机实验中是否发生是随机的,是不能预知的,随着试验次数的增多,频率越来越稳定于概率.
学校是一个相对消费稳定的地方,每个学生根据自己的实际情况每个月的消费应该相对固定,出现题中这种现象可能是发生了“小概率事件”.
本题以支付方式相关调查来设置问题,考查概率统计在生活中的应用,考查概率的定义和分布列的应用,使学生体会到数学与现实生活息息相关.
20.(Ⅰ);(Ⅱ);(Ⅲ)1人.
记甲、乙、丙三人100米跑成绩合格分别为事件,,,显然事件,,相互独立,则,,,从而根据不同事件的概率求法求得各小题.
【详解】
记甲、乙、丙三人100米跑成绩合格分别为事件,,,
显然事件,,相互独立,则,,
设恰有人合格的概率为.
(Ⅰ)三人都合格的概率:
(Ⅱ)三人都不合格的概率:.
(Ⅲ)恰有两人合格的概率:.
恰有一人合格的概率:.
因为,
所以出现1人合格的概率最大.
21.(1);(2);(3).
(1)由频率分布直方图的高之和为组距分之一,即可得出结果;
(2)根据样本容量、总体与频率之间的关系计算即可得出结果;
(3)用总面积1减去左边2个矩形的面积即可.
【详解】
解:(1)由频率分布直方图的性质得:
,
解得.
(2)∵成绩在的学生人数为6,
由频率分布直方图得成绩在的学生所占频率为:,
∴.
(3)根据样本估计“该校高一学生期末数学考试成绩70”的概率:
.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,则摸出白球个数多于黑球个数的概率为( )
A. B. C. D.
2.某同学从家到学校要经过三个十字路口,设各路口信号灯工作相互独立,该同学在各路口遇到红灯的概率分别为,,,则该同学从家到学校至少遇到一次红灯的概率为( )
A. B. C. D.
3.下列说法错误的是( )
A.随机事件的概率与频率是一样的
B.在试验中,某事件发生的频率的取值范围是
C.必然事件的概率是1
D.不可能事件的概率是0
4.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A. B. C. D.
5.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.某天,齐王与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜,则田忌获胜概率为( ).
A. B. C. D.
6.以下三个命题:
①对立事件也是互斥事件;
②一个班级有50人,男生与女生的比例为3:2,利用分层抽样的方法,每个男生被抽到的概率为,每个女生被抽到的概率为;
③若事件,,两两互斥,则.
其中正确命题的个数为( )
A.0 B.1 C.2 D.3
7.甲、乙两人投篮,投中的概率分别为0.6,0.7,若两人各投2次,则两人投中次数不等的概率是( )
A.0.6076 B.0.7516 C.0.3924 D.0.2484
8.已知100件产品中有5件次品,从这100件产品中任意取出3件,设表示事件“3件产品 全不是次品”,表示事件“3件产品全是次品”,表示事件“3件产品中至少有1件是 次品”,则下列结论正确的是( )
A.与互斥 B.与互斥但不对立
C.任意两个事件均互斥 D.与对立
9.对关于的一元二次方程,通过掷骰子确定其中的系数,第一次出现的数作为,第二次出现的数作为(一颗骰子有6个面,分别刻有1、2,3、4、5、6六个数,每次扰掷,各数出现的可能性相同),那么,这个方程有解的概率是( )
A. B. C. D.
10.下列事件A,B是独立事件的是( )
A.一枚硬币掷两次,A=“第一次为正面向上”,B=“第二次为反面向上”
B.袋中有两个白球和两个黑球,不放回地摸两球,A=“第一次摸到白球”,B=“第二次摸到白球”
C.掷一枚骰子,A=“出现点数为奇数”,B=“出现点数为偶数”
D.A=“人能活到20岁”,B=“人能活到50岁”
11.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
12.掷一枚骰子的试验中,出现各点的概率均为,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A+(表示事件B的对立事件)发生的概率为( )
A. B. C. D.
二、填空题
13.若同时掷两颗骰子,则出现两颗骰子的点数之和大于9的概率为________
14.甲 乙两名同学进行篮球投篮练习,甲同学一次投篮命中的概率为,乙同学一次投篮命中的概率为,假设两人投篮命中与否互不影响,则甲 乙两人各投篮一次,至少有一人命中的概率是___________.
15.某产品分甲、乙、丙三级,其中甲级属正品,乙、丙两级属次品.若生产中出现乙级产品的概率为0.03,出现丙级产品的概率为0.01,则对成品任意抽查一件抽得正品的概率为__________.
16.已知A,B是相互独立事件,且,,则________.
三、解答题
17.今年中国共产党迎来了建党100周年,为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀,某区组织了党史知识竞赛活动.在最后一轮晋级比实中,甲、乙、丙三所学校回答一道有关红色革命根据地建立时间的问题,已知甲校回答正确这道题的概率为,甲、丙两所学校都回答正确这道题的概率是,乙、丙两所学校都回答正确这道题的概率是.若各学校回答这道题是否正确是互不影响的.
(1)求乙、丙两所学校各自回答正确这道题的概率;
(2)求甲、乙、丙三所学校中不少于2所学校回答正确这道题的概率.
18.在2016珠海航展志愿服务开始前,团珠海市委调查了北京师范大学珠海分校某班50名志愿者参加志愿服务礼仪培训和赛会应急救援培训的情况,数据如下表:单位:人
参加志愿服务礼仪培训 未参加志愿服务礼仪培训
参加赛会应急救援培训 8 8
未参加赛会应急救援培训 4 30
(1)从该班随机选1名同学,求该同学至少参加上述一个培训的概率;
(2)在既参加志愿服务礼仪培训又参加赛会应急救援培训的8名同学中,有5名男同学A,A,A,A,A名女同学B,B,B现从这5名男同学和3名女同学中各随机选1人,求A被选中且B未被选中的概率.
19.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
交付金额(元) 支付方式 (0,1000] (1000,2000] 大于2000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
20.某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13s内(称为合格)的概率分别为,,.若对这三名短跑运动员的100跑的成绩进行一次检测,则求:
(Ⅰ)三人都合格的概率;
(Ⅱ)三人都不合格的概率;
(Ⅲ)出现几人合格的概率最大.
21.某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在的学生人数为6.
(1)求直方图中的值;
(2)求的值;
(3)试根据样本估计“该校高一学生期末数学考试成绩70”的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
根据古典概型的概念及计算公式直接计算即可.
【详解】
一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,
基本事件总数,
摸出白球个数多于黑球个数包含的基本事件个数,
则摸出白球个数多于黑球个数的概率为,
故选:C.
2.D
利用相互独立事件的概率乘法公式及对立事件的概率公式即可求解.
【详解】
解:由题意,该同学从家到学校至少遇到一次红灯的概率为,
故选:D.
3.A
依据频率和概率,必然事件和不可能事件的定义,依次判断即可
【详解】
对于选项A,概率是唯一的确定的值,而频率是统计出来的,通过一次次的试验得到,因此随机事件的概率与频率是两个不同的概念,故A错误;
对于选项B,频率是指是指每个对象出现的次数与总次数的比值,故取值范围是,故B正确;
对于选项C,D,由必然事件和不可能事件的定义可知,说法正确.
故选:A
4.D
根据题意,写出所有抽取的基本事件,再找出满足题意的基本事件,利用古典概型的概率计算公式即可求得结果.
【详解】
根据题意,不妨用表示两次抽取的基本事件,
其中代表第一次抽取的数字,代表第二次抽取的数字.
故所有抽取的可能有如下种:
满足抽得的第一张卡片上的数大于第二张卡片上的数的有如下种:
,
根据古典概型的概率计算公式可得:该事件的概率.
故选:D.
5.B
设齐王的三匹马分别为,田忌的三匹马分别为,列举所有比赛的情况,利用古典概型的概率公式计算即可得出结果.
【详解】
设齐王的三匹马分别为,田忌的三匹马分别为,所有比赛的情况::
、、,齐王获胜三局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,田忌获胜两局;
、、,齐王获胜两局,共6种情况,则田忌胜1种情况,故概率为
故选:B
本题考查了古典概型的概率计算问题,考查了理解辨析和数学运算能力,属于中档题目.
6.B
由对立事件的定义可判断①;由分层抽样的定义可判断②;由互斥事件的概率理解可判断③.
【详解】
对于①,由对立事件的定义可知对立事件一定是互斥事件,故①正确;
对应②,可知该班有男生30人,女生20人,由于不知道需要抽取多少人,所以无法得出概率,故②错误;
对应③,事件,,不一定包含所有事件,故,故③错误.
故选:B.
本题考查考查对事件互斥、对立的理解,考查对分层抽样的理解,属于基础题.
7.A
先求出两人投中次数相等的概率,再根据对立事件的概率公式可得两人投中次数不相等的概率.
【详解】
两人投中次数相等的概率P=,
故两人投中次数不相等的概率为:1﹣0.3924=0.6076.
故选:A.
本题考查了对立事件的概率公式和独立事件的概率公式,属于基础题.
8.D
列出基本事件,再结合互斥事件,对立事件的定义即可判断.
【详解】
设1表示取到正品, 0 表示取到次品,所有事件
则
故与不互斥,故A,C错
故与互斥且对立,故B错,D正确
故选:D
9.C
记事件 “方程有实根”.由,得:,利用列举法得到事件包含的基本事件的个数,又总的基本事件共个,由古典概型概率公式求出方程有解的概率.
【详解】
记事件 “方程有实根”.
由,得:
又基本事件共个,
其中事件包含19个基本事件,列举如下:
,,,,,,,,,,,,
,,,,,,,
所以,
故选:C.
10.A
利用相互独立事件的概念,对四个选项逐一分析排除,从而得出正确选项.
【详解】
对于A选项,两个事件发生,没有关系,故是相互独立事件.对于B选项,事件发生时,影响到事件,故不是相互独立事件.对于C选项,由于投的是一个骰子,是对立事件,所以不是相互独立事件.对于D选项,能活到岁的,可能也能活到岁,故不是相互独立事件.综上所述,本小题选A.
本小题主要考查相互独立事件的概念以及相互独立事件的识别,属于基础题.
11.A
事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】
事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
12.C
由题意知试验发生包含的所有事件共有6种,事件和事件是互斥事件,看出事件和事件包含的基本事件数,根据互斥事件和古典概型概率公式得到结果.
【详解】
解:事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:C.
13.
列举基本事件,直接套公式求概率.
【详解】
同时掷两颗骰子,有共36种情况;
而点数之和大于9包括共6种,
所以两颗骰子的点数之和大于9的概率为.
故答案为:.
14.
考虑两个人都不命中的概率,从而可求至少有一个人命中的概率.
【详解】
两个都不命中的概率为,
故至少有一人命中的概率是,
故答案为:.
15.0.96
根据题意,设抽取产品的等级分别为事件、、,且事件,,彼此互斥,根据概率事件加法公式,即可求解.
【详解】
记“抽出的产品为正品”为事件,“抽出的产品为乙级产品”为事件,“抽出的产品为丙级产品”为事件,则事件,,彼此互斥,且与是对立事件,所以.
故答案为:
本题考查对立事件概率公式,属于基础题.
16.
首先计算出事件和的概率,再根据相互独立事件同时发生的概率计算公式即可得结果.
【详解】
∵,,∴,.
又∵A,B是相互独立事件,∴和也为相互独立事件,
∴,
故答案为:.
本题主要考查相互独立事件的概率乘法公式,关键是理解“事件A与事件B相互独立”的意义,属于基础题.
17.(1)
(2)
(1)根据独立事件的概率公式计算;
(2)结合互斥事件、独立事件的概率公式计算.
(1)
设事件“甲学校回答正确这道题”,事件“乙学校回答正确这道题”,事件“丙学校回答正确这道题” ,
则,,,
∵各学校回答这道题是否正确是互不影响的.
∴事件A,B,C相互独立.
∴,
∴ ;
(2)
设事件“甲、乙、丙三所学校中不少于2所学校回答正确这道题”且两两互斥,
;
由于事件A,B,C相互独立.
所以
,
,
,
18.(1);(2).
(1)根据表中数据知未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,故至少参加上述一个培训的共有人.从而求得概率;
(2)从这5名男同学和3名女同学中各随机选1人,列出其一切可能的结果,从而求得被选中且未被选中的概率.
【详解】
解:由调查数据可知,既未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,
故至少参加上述一个培训的共有人.
从该班随机选1名同学,该同学至少参加上述一个培训的概率为;
从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的基本事件有:
,
,
,
共15个,
根据题意,这些基本事件的出现是等可能的,
事件“被选中且未被选中”所包含的基本事件有:,共2个,
被选中且未被选中的概率为.
19.(Ⅰ) ;
(Ⅱ)见解析;
(Ⅲ)见解析.
(Ⅰ)由题意利用古典概型计算公式可得满足题意的概率值;
(Ⅱ)首先确定X可能的取值,然后求得相应的概率值可得分布列,最后求解数学期望即可.
(Ⅲ)由题意结合概率的定义给出结论即可.
【详解】
(Ⅰ)由题意可知,两种支付方式都是用的人数为:人,则:
该学生上个月A,B两种支付方式都使用的概率.
(Ⅱ)由题意可知,
仅使用A支付方法的学生中,金额不大于1000的人数占,金额大于1000的人数占,
仅使用B支付方法的学生中,金额不大于1000的人数占,金额大于1000的人数占,
且X可能的取值为0,1,2.
,,,
X的分布列为:
X 0 1 2
其数学期望:.
(Ⅲ)我们不认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化.理由如下:
随机事件在一次随机实验中是否发生是随机的,是不能预知的,随着试验次数的增多,频率越来越稳定于概率.
学校是一个相对消费稳定的地方,每个学生根据自己的实际情况每个月的消费应该相对固定,出现题中这种现象可能是发生了“小概率事件”.
本题以支付方式相关调查来设置问题,考查概率统计在生活中的应用,考查概率的定义和分布列的应用,使学生体会到数学与现实生活息息相关.
20.(Ⅰ);(Ⅱ);(Ⅲ)1人.
记甲、乙、丙三人100米跑成绩合格分别为事件,,,显然事件,,相互独立,则,,,从而根据不同事件的概率求法求得各小题.
【详解】
记甲、乙、丙三人100米跑成绩合格分别为事件,,,
显然事件,,相互独立,则,,
设恰有人合格的概率为.
(Ⅰ)三人都合格的概率:
(Ⅱ)三人都不合格的概率:.
(Ⅲ)恰有两人合格的概率:.
恰有一人合格的概率:.
因为,
所以出现1人合格的概率最大.
21.(1);(2);(3).
(1)由频率分布直方图的高之和为组距分之一,即可得出结果;
(2)根据样本容量、总体与频率之间的关系计算即可得出结果;
(3)用总面积1减去左边2个矩形的面积即可.
【详解】
解:(1)由频率分布直方图的性质得:
,
解得.
(2)∵成绩在的学生人数为6,
由频率分布直方图得成绩在的学生所占频率为:,
∴.
(3)根据样本估计“该校高一学生期末数学考试成绩70”的概率:
.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
