福建省清流一中2011-2012学年高二10月月考数学试题
文档属性
| 名称 | 福建省清流一中2011-2012学年高二10月月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-22 10:48:44 | ||
图片预览



文档简介
清流一中2011-2012学年第一学期高二数学
第一阶段试卷
一、选择题(本题共12小题,每小题5分,共60分)
1.现要完成下列3项抽样调查,
①从10盒酸奶中抽取3盒进行食品卫生检查.②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.③某中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员2名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本. 较为合理的抽样方法是( )
A.①系统抽样,②简单随机抽样,③分层抽样;
B.①简单随机抽样,②分层抽样,③系统抽样;
C.①简单随机抽样,②系统抽样,③分层抽样;
D.①分层抽样,②系统抽样,③简单随机抽样.
2. 用“辗转相除法”求得和的最大公约数是( )
A. B. C. D.
3.假设a=123,那么在执行b=a/10-a10后b的值为 ( )
A.0 B.12 C.3 D.0.3
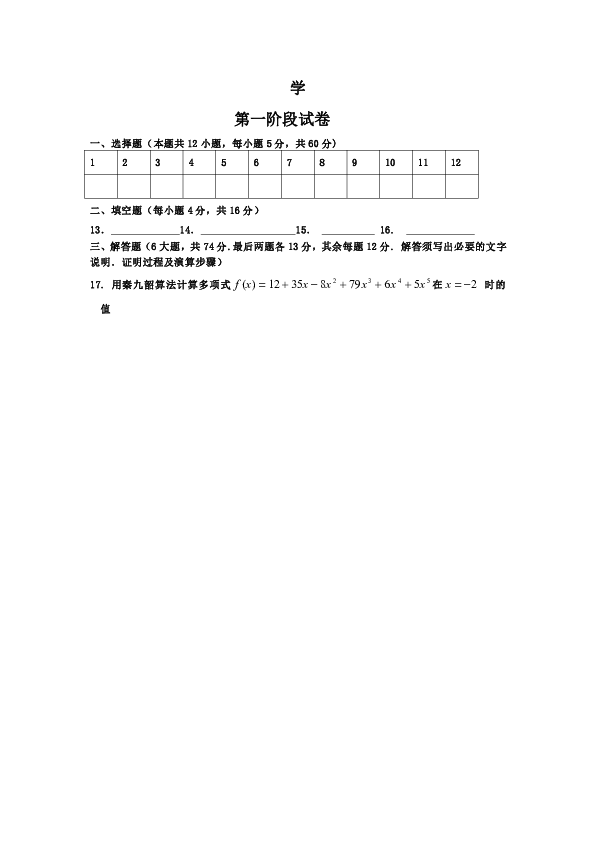
4.某市高三数学调研考试中,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为90,那么90~100分数段的人数为( )
A.630 B.720
C.810 D.900
5. 将两个数a=2, b= -6交换,使a= -6, b=2,下列语句正确的( )
A. B. C. D.
6 某企业有职工人,其中高级职称人,中级职称人,一般职员人,
现抽取人进行分层抽样,则各职称人数分别为( )
A B C D
7 4.从个同类产品(其中个是正品,个是次品)中任意抽取个的必然事件是( )
个都是正品 B.至少有个是次品
C. 个都是次品 D.至少有个是正品
8.下列说法中,正确的是( )
(1)数据4、6、6、7、9、4的众数是4。
(2)平均数、众数与中位数从不同的角度描述了一组数据的集中趋势。
(3)平均数是频率分布直方图的“重心”。
(4)频率分布直方图中各小长方形的面积等于相应各组的频数。
A.(1)(2)(3) B.(2)(3) C.(2)(4) D.(1)(3)(4)
9. 当时,下面的程序段结果是 ( )
A. B. C. D.
10. 某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,那么互斥不对立的两个事件是 ( )
A. 至少有1名男生与全是女生
B. 至少有1名男生与全是男生
C.至少有1名男生与至少有1名女生
D.恰有1名男生与恰有2名女生
11. 从2 008名学生中选取50名学生参加数学竞赛,若采用下面的方法选取:先用简单随机抽样从2 008人中剔除8人,剩下的2 000人再按系统抽样的方法抽取50人,则在2 008人中,每人入选的机会 ( )
A.不全相等 B.均不相等 C. 都相等,且为 D.都相等,且为
12. 数据的平均数为1,标准差为2,则数据,,,…,的平均数与标准差分别为( )
A.-1,4 B.-1,2 C.2,4 D.2,-1
二、填空题(每小题4分,共 16分)
13.同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是 。
14. 把六进制数转换成三进制数:= .
15.阅读如右所示的程序框图,若输入,,则输出 ,i= .
16.现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6, 2.7, 2.8, 2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3 m的概率为 .
清流一中2011-2012学年第一学期高二数学
第一阶段试卷
一、选择题(本题共12小题,每小题5分,共60分)
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题(每小题4分,共16分)
13. 14. 15. 16.
三、解答题(6大题,共74分.最后两题各13分,其余每题12分. 解答须写出必要的文字说明.证明过程及演算步骤)
17. 用秦九韶算法计算多项式在 时的值
18.根据下面的要求,求值.
(Ⅰ)请完成执行该问题的程序框图;(Ⅱ)以下是解决该问题的程序,请完成执行该问题的程序.
19.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由
20. 袋中有红、黄、白3种颜色的球各一个,从中抽取一个,有放回的抽取3次,求:
(1)3个全是红球的概率;(2)3个颜色全相同的概率;(3)3个颜色不全相同的概率;
21. ( 13分)某城市理论预测2000年到2004年人口数与年份的关系如下表所示
年份200(年)
0
1
2
3
4
人口数(十万)
5
7
8
11
19
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)据此估计2005年该城市人口总数。
参考公式:
22.对某电子元件进行寿命追踪调查,情况如下.
寿命(h)
100~200
200~300
300~400
400~500
500~600
个 数
20
30
80
40
30
(1)列出频率分布表;
(2)画出频率分布直方图及频率分布折线图;
(3)从频率分布直方图可以算出电子元件寿命的众数、中位数和平均数是多少?
解:(1)样本频率分布表如下.
寿命(h)
频 数
频 率
100~200
200~300
300~400
400~500
500~600
合 计
(2)频率分布直方图如下.
(3)
清流一中2011-2012学年第一学期高二数学答案
一.选择:
1--5 CDDCB 6--10 BDBCD 11—12 CA
二.填空:
13.1/4 14.2220(3) 15.12,3 16.1/5
17.
=((((5x+6)x+79)x-8)x+35)x+12 4分
V0=5 5分
V1=5*(-2)+6=-4 6分
V2=V1*(-2)+79=87 7分
V3=v2*(-2)-8=-182 8分
V4=V3*(-2)+35=-329 9分
V5=V4*(-2)+12=670 10分
所以当x=-2时,f(x)=670 12分
18.解:(1)程序框图如图所示:
19.解
5分
(2)
10分
∵,,∴甲的成绩较稳定,派甲参赛比较合适 12分
20.解:基本事件总数是3*3*3=27 (1) 3个全是红球的事件数是1,所以P=1/27 4分(2) 3个颜色全相同的事件数是3,所以P=1/9 8分(3) 3个颜色不全相同与3个颜色全相同的事件是对立事件,所以P=1-1/9=8/9 12分
21. 解:(1)图略 5分
Xi
Yi
XiYi
Xi︿2
1
0
5
0
0
2
1
7
7
1
3
2
8
16
4
4
3
11
33
9
5
4
19
76
16
合计
10
50
132
30
X的平均数为2,Y的平均数为10
b=(132-5*2*10)/(30-5*4)=3.2
a=10-3.2*2=3.6
故Y关于x的线性回归方程为 y=3.2x+3.6 11分
(3)x=5,y=196(万)
据此估计2005年.该 城市人口总数196(万) 13分
22.(1)4分(2)9分(3)从频率分布直方图可以看出电子元件寿命的众数是350;设距离300的x单位处是中位数,则依题意得0.004x=0.5-0.1-0.15解得x=62.5,所以中位数是362.5;平150*0.10+250*0.15+350*0.40+450*0.20+550*0.15=365
第一阶段试卷
一、选择题(本题共12小题,每小题5分,共60分)
1.现要完成下列3项抽样调查,
①从10盒酸奶中抽取3盒进行食品卫生检查.②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.③某中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员2名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本. 较为合理的抽样方法是( )
A.①系统抽样,②简单随机抽样,③分层抽样;
B.①简单随机抽样,②分层抽样,③系统抽样;
C.①简单随机抽样,②系统抽样,③分层抽样;
D.①分层抽样,②系统抽样,③简单随机抽样.
2. 用“辗转相除法”求得和的最大公约数是( )
A. B. C. D.
3.假设a=123,那么在执行b=a/10-a10后b的值为 ( )
A.0 B.12 C.3 D.0.3
4.某市高三数学调研考试中,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若130~140分数段的人数为90,那么90~100分数段的人数为( )
A.630 B.720
C.810 D.900
5. 将两个数a=2, b= -6交换,使a= -6, b=2,下列语句正确的( )
A. B. C. D.
6 某企业有职工人,其中高级职称人,中级职称人,一般职员人,
现抽取人进行分层抽样,则各职称人数分别为( )
A B C D
7 4.从个同类产品(其中个是正品,个是次品)中任意抽取个的必然事件是( )
个都是正品 B.至少有个是次品
C. 个都是次品 D.至少有个是正品
8.下列说法中,正确的是( )
(1)数据4、6、6、7、9、4的众数是4。
(2)平均数、众数与中位数从不同的角度描述了一组数据的集中趋势。
(3)平均数是频率分布直方图的“重心”。
(4)频率分布直方图中各小长方形的面积等于相应各组的频数。
A.(1)(2)(3) B.(2)(3) C.(2)(4) D.(1)(3)(4)
9. 当时,下面的程序段结果是 ( )
A. B. C. D.
10. 某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,那么互斥不对立的两个事件是 ( )
A. 至少有1名男生与全是女生
B. 至少有1名男生与全是男生
C.至少有1名男生与至少有1名女生
D.恰有1名男生与恰有2名女生
11. 从2 008名学生中选取50名学生参加数学竞赛,若采用下面的方法选取:先用简单随机抽样从2 008人中剔除8人,剩下的2 000人再按系统抽样的方法抽取50人,则在2 008人中,每人入选的机会 ( )
A.不全相等 B.均不相等 C. 都相等,且为 D.都相等,且为
12. 数据的平均数为1,标准差为2,则数据,,,…,的平均数与标准差分别为( )
A.-1,4 B.-1,2 C.2,4 D.2,-1
二、填空题(每小题4分,共 16分)
13.同时抛掷两枚质地均匀的硬币,则出现两个正面朝上的概率是 。
14. 把六进制数转换成三进制数:= .
15.阅读如右所示的程序框图,若输入,,则输出 ,i= .
16.现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6, 2.7, 2.8, 2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3 m的概率为 .
清流一中2011-2012学年第一学期高二数学
第一阶段试卷
一、选择题(本题共12小题,每小题5分,共60分)
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题(每小题4分,共16分)
13. 14. 15. 16.
三、解答题(6大题,共74分.最后两题各13分,其余每题12分. 解答须写出必要的文字说明.证明过程及演算步骤)
17. 用秦九韶算法计算多项式在 时的值
18.根据下面的要求,求值.
(Ⅰ)请完成执行该问题的程序框图;(Ⅱ)以下是解决该问题的程序,请完成执行该问题的程序.
19.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由
20. 袋中有红、黄、白3种颜色的球各一个,从中抽取一个,有放回的抽取3次,求:
(1)3个全是红球的概率;(2)3个颜色全相同的概率;(3)3个颜色不全相同的概率;
21. ( 13分)某城市理论预测2000年到2004年人口数与年份的关系如下表所示
年份200(年)
0
1
2
3
4
人口数(十万)
5
7
8
11
19
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)据此估计2005年该城市人口总数。
参考公式:
22.对某电子元件进行寿命追踪调查,情况如下.
寿命(h)
100~200
200~300
300~400
400~500
500~600
个 数
20
30
80
40
30
(1)列出频率分布表;
(2)画出频率分布直方图及频率分布折线图;
(3)从频率分布直方图可以算出电子元件寿命的众数、中位数和平均数是多少?
解:(1)样本频率分布表如下.
寿命(h)
频 数
频 率
100~200
200~300
300~400
400~500
500~600
合 计
(2)频率分布直方图如下.
(3)
清流一中2011-2012学年第一学期高二数学答案
一.选择:
1--5 CDDCB 6--10 BDBCD 11—12 CA
二.填空:
13.1/4 14.2220(3) 15.12,3 16.1/5
17.
=((((5x+6)x+79)x-8)x+35)x+12 4分
V0=5 5分
V1=5*(-2)+6=-4 6分
V2=V1*(-2)+79=87 7分
V3=v2*(-2)-8=-182 8分
V4=V3*(-2)+35=-329 9分
V5=V4*(-2)+12=670 10分
所以当x=-2时,f(x)=670 12分
18.解:(1)程序框图如图所示:
19.解
5分
(2)
10分
∵,,∴甲的成绩较稳定,派甲参赛比较合适 12分
20.解:基本事件总数是3*3*3=27 (1) 3个全是红球的事件数是1,所以P=1/27 4分(2) 3个颜色全相同的事件数是3,所以P=1/9 8分(3) 3个颜色不全相同与3个颜色全相同的事件是对立事件,所以P=1-1/9=8/9 12分
21. 解:(1)图略 5分
Xi
Yi
XiYi
Xi︿2
1
0
5
0
0
2
1
7
7
1
3
2
8
16
4
4
3
11
33
9
5
4
19
76
16
合计
10
50
132
30
X的平均数为2,Y的平均数为10
b=(132-5*2*10)/(30-5*4)=3.2
a=10-3.2*2=3.6
故Y关于x的线性回归方程为 y=3.2x+3.6 11分
(3)x=5,y=196(万)
据此估计2005年.该 城市人口总数196(万) 13分
22.(1)4分(2)9分(3)从频率分布直方图可以看出电子元件寿命的众数是350;设距离300的x单位处是中位数,则依题意得0.004x=0.5-0.1-0.15解得x=62.5,所以中位数是362.5;平150*0.10+250*0.15+350*0.40+450*0.20+550*0.15=365
同课章节目录
