椭圆的几何性质
图片预览



文档简介
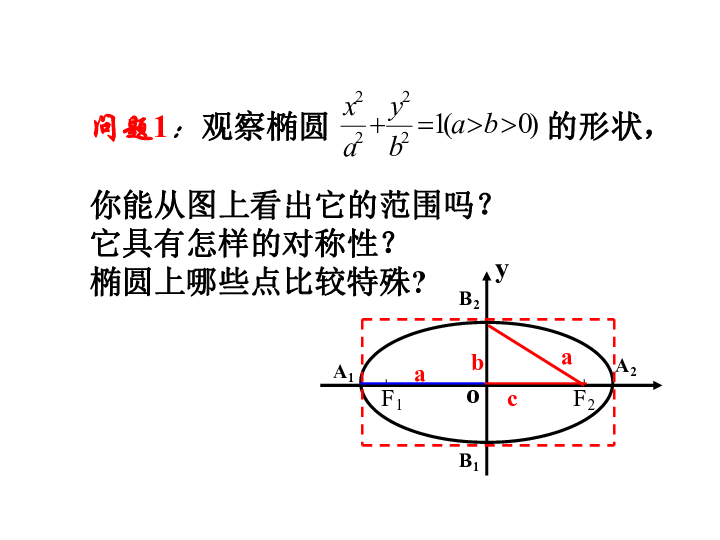
课件15张PPT。椭圆的简单几何性质(1)问题1:观察椭圆 的形状,
你能从图上看出它的范围吗?
它具有怎样的对称性?
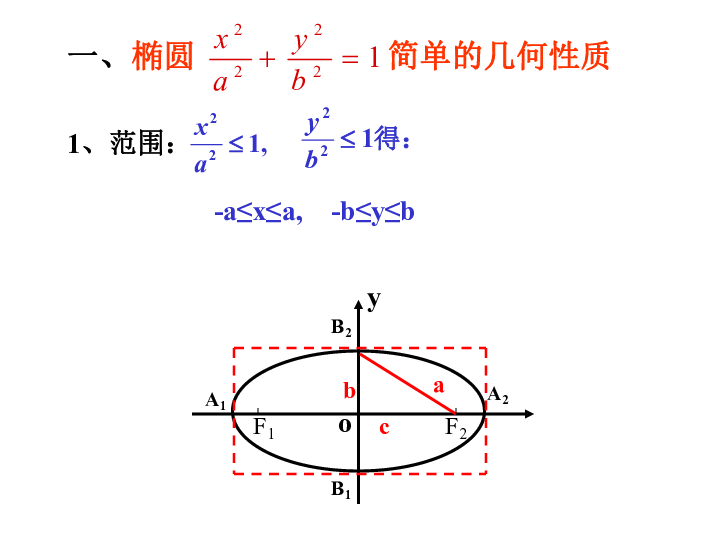
椭圆上哪些点比较特殊?a1、范围:
-a≤x≤a, -b≤y≤b
2、对称性:从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。3、椭圆的顶点令 x=0,得 y=?说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。已知椭圆方程为它的长轴长是: 。短轴是: 。
焦距是: .
焦点坐标是: 。
顶点坐标是: 。
6例1:回答下列问题,并用描点法画出椭圆图形。问题2:圆的形状都是相同的,而椭圆却有些比较“扁”,有些比较“圆”,用什么样的量来刻画椭圆“扁”的程度呢?练习:下列各组椭圆中,哪一个更接近于圆? a2=b2+c2例2:若椭圆 + =1的离心率为 0.5,求k的值分
类
讨
论
的
思
想巩固练习:1. 若点P(x,y)在椭圆上,则点P(x,y)横坐标x的取值范围 ? 3. 中心在原点,焦点在x轴上,长轴、短轴的长分别为8和6的椭圆方程为 ?
4.说出椭圆 的长轴长,短轴长,顶点和焦点坐标 5 若椭圆的两个焦点把长轴分成三等分,则其离心率为 ?
2.若点P(2,4)在椭圆 上,下列是椭圆上的点有
(1)P(-2,4) (2)P(-4,2)
(3) P(-2,-4) (4)P(2,-4)问题探究:若椭圆 的两个
焦点及一个短轴端点构成正三角形,求其离心率。变式:若是等边三角形?基本量a,b,c,e
及顶点、焦点、对称中心及其相互之间的关系小结:1.知识小结:
(1) 学习了椭圆的范围、对称性、顶点坐标、离心率等概念及其几何意义。
(2) 研究了椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系
2.数学思想方法:
(1)数与形的结合,用代数的方法解决几何问题。
(2)分类讨论的数学思想
你能从图上看出它的范围吗?
它具有怎样的对称性?
椭圆上哪些点比较特殊?a1、范围:
-a≤x≤a, -b≤y≤b
2、对称性:从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。3、椭圆的顶点令 x=0,得 y=?说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。已知椭圆方程为它的长轴长是: 。短轴是: 。
焦距是: .
焦点坐标是: 。
顶点坐标是: 。
6例1:回答下列问题,并用描点法画出椭圆图形。问题2:圆的形状都是相同的,而椭圆却有些比较“扁”,有些比较“圆”,用什么样的量来刻画椭圆“扁”的程度呢?练习:下列各组椭圆中,哪一个更接近于圆? a2=b2+c2例2:若椭圆 + =1的离心率为 0.5,求k的值分
类
讨
论
的
思
想巩固练习:1. 若点P(x,y)在椭圆上,则点P(x,y)横坐标x的取值范围 ? 3. 中心在原点,焦点在x轴上,长轴、短轴的长分别为8和6的椭圆方程为 ?
4.说出椭圆 的长轴长,短轴长,顶点和焦点坐标 5 若椭圆的两个焦点把长轴分成三等分,则其离心率为 ?
2.若点P(2,4)在椭圆 上,下列是椭圆上的点有
(1)P(-2,4) (2)P(-4,2)
(3) P(-2,-4) (4)P(2,-4)问题探究:若椭圆 的两个
焦点及一个短轴端点构成正三角形,求其离心率。变式:若是等边三角形?基本量a,b,c,e
及顶点、焦点、对称中心及其相互之间的关系小结:1.知识小结:
(1) 学习了椭圆的范围、对称性、顶点坐标、离心率等概念及其几何意义。
(2) 研究了椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系
2.数学思想方法:
(1)数与形的结合,用代数的方法解决几何问题。
(2)分类讨论的数学思想
