30°、45°、60°角的三角比

9.2 300,450,600角的三角比
山东省单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一 学习目标：
1掌握300,450,600角的三角比，能够用它进行计算。
2能够根据300,450,600的三角比的值，求出相应锐角的大小。
3能够运用300,450,600角的三角比解决问题。
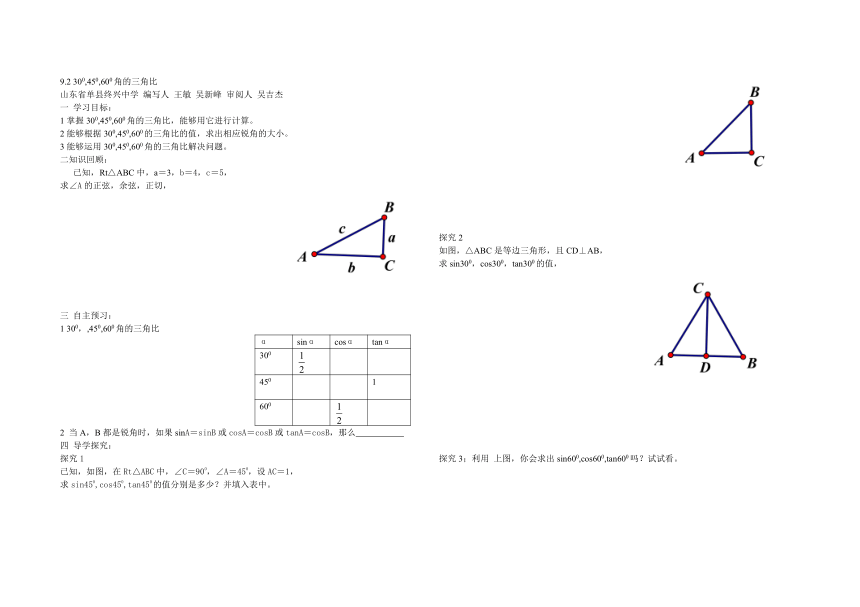
二知识回顾：
已知，Rt△ABC中，a＝3，b＝4，c＝5，
求∠A的正弦，余弦，正切，
三 自主预习：
1 300，,450,600角的三角比
α
sinα
cosα
tanα
300
450
1
600
2 当A，B都是锐角时，如果sinA＝sinB或cosA＝cosB或tanA＝cosB，那么
四 导学探究：
探究1
已知，如图，在Rt△ABC中，∠C＝900，∠A＝450，设AC＝1，
求sin450,cos450,tan450的值分别是多少？并填入表中。
探究2
如图，△ABC是等边三角形，且CD⊥AB，
求sin300，cos300，tan300的值，
探究3；利用 上图，你会求出sin600,cos600,tan600吗？试试看。
想一想：sin300与cos600时什么关系，cos300与sin600什么关系？由此，你得出什么结论？并说明理由。
例 计算，(1) （－2）2＋tan450－2cos600 （2）sin600－cos450＋
练一练：
求下列各式的值
1 sin300＋cos600； 2 tan300×tan600； 3 2 sin600－tan300 4 sin450×cos450＋tan450
五 当堂达标：
1 在直角坐标系中，点P（4，y）在第一象限内，且OP与x轴正半轴的夹角为600，则y的值 是 （ ）
A B 4 C 8 D 2
2 在△ABC中，∠A，∠B，都是锐角，且sinA＝，cosB＝，△ABC三个角的大小关系是 （ ）
A ∠C＞∠A＞∠B B ∠B＞∠C＞∠A C ∠A＞∠B＞∠C D∠C＞∠B＞∠A
3 如图，线段OA在第二象限，A点的坐标为（－4,4），OA与y轴的夹角为α ，则cosα＝
4 锐角∠A满足2sin（A－150）＝，则∠A＝
5 ，若（tanA-）2+（tanB-）2=0，∠A，∠B为⊿ABC的内角，则⊿ABC的形状是
。
6计算： (2cos450﹣sin600)+
7计算 cos300×tan300+tan450×sin600
8计算 ﹣4sin600+(4-m)0(m≠4)
9.2 《30°、45°、60°角的三角比》
【教学目标】
1、经历探索30°、45°、60°角的三角比的过程，熟记这些角三角比。
2、会计算含有特殊角的三角比的式子的值。
3、能根据三角比的值求出角的度数。
【重点与难点】会计算含有特殊角的三角比的式子的值。
【教学过程】
一、温故知新：
1．锐角A的 、 、 统称锐角A的三角比．

∠ A的正弦：
∠A的余弦：
∠A的正切：

2．一个锐角的三角比只与 有关．
二、课内探究：
【探究一】：sin45°,cos45 °,tan45 °的值分别是多少？

【探究二】：sin30°,cos30 °,tan30 °的值分别是多少？
取两个含30°角的大小相等的三角尺，按图中的方式拼在一起，得到的△ABC是怎样的三角形？为什么？
A

B D C
【探究三】：利用上图，你会求出60°的正弦、余弦、正切的值吗？
三、观察与思考：
30°
45°
60°
sin
cos
tan
从填写的表格中，你发现了哪些规律？
四、新知应用：
1、求下列各式的值：
（1）sin30°·cos45 （2）tan45 °－cos60°. 2、在Rt△ABC中，已知sinA= ,求锐角A的度数．
五、课堂小结：
六、随堂检测：（见多媒体）
七、布置作业：
必做题:课本P68 A组 1、2 选做题:课本P68 B组 1、2