北师大版八年级下册6 一元一次不等式组课件(共37张PPT)
文档属性
| 名称 | 北师大版八年级下册6 一元一次不等式组课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 754.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
2.6.1 一元一次不等式组
第二章 一元一次不等式与一元一次不等式组
课前提问(1分钟)
1.下列不等式中,是一元一次不等式的有( )个.
①x>-3;②xy≥1;③
;④
;⑤
A. 1 B. 2 C. 3 D. 4
B
2.
1
2022/5/4
3
1.理解一元一次不等式组、一元一次不等式组
的解集、解不等式组等概念.
2.会解一元一次不等式组,并会用数轴确定解集.
学习目标 (1分钟)
4、求 ,叫做解不等式组.
2、一元一次不等式组中 ,
就叫做这个一元一次不等式组的解集.
3、不等式组 中,不等式4(x+5)>100的
解集为 ,不等式4(x-5)<68的集解为 .
在同一数轴上可以表示为 不等式组
的解集为 .
阅读课本P54的内容,回答下列问题:
1、一般地,关于 的 合在
一起,就组成一元一次不等式组.
同一未知数
几个一元一次不等式
各个不等式的解集的公共部分
学生自学,教师巡视(3分钟)
x>20
x<22
20< x<22
20
0
22
不等式组解集的过程
自学指导1:(1分钟)
3. 一台装载机每时可装载石料50t,一堆石料的质量在1800t到2200t之间,那么这台装载机大约要用多长时间才能将这堆石料装完,设用x小时可以装完,则_____________________.(只列式)
自学检测1 (5分钟)
1.下列选项中是一元一次不等式组的是( )
D
D
2. 不等式组 的解集在数轴上可表示为( )
易错点:一元一次不等式组的判定:①未知数的个数:1;②未知数的次数:1;③左右两边都是整式;④符号:不等号
1.例1中不等式组的解集与不等式①和不等式②的解集
有何关系?
2.解一元一次不等式组的解题过程分为:
6
自学指导2(1分钟)
阅读例1的解答过程:回答下列问题
学生自学,教师巡视:3分钟
③表示这个不等式组的解集.
②利用数轴求出这些不等式解集的公共部分.
①求出这个不等式组中各个不等式的解集.
解:解不等式①得
解不等式②得
在同一条数轴上表示不
等式① ②的解集,如图:
∴原不等式组的解集为:
① ②
① ②
解:解不等式①得
解不等式②得
在同一条数轴上表示不
等式① ②的解集,如图:
∴原不等式组的解集为:
-2 -1 0 1 2
解下列不等式组:
自学检测2 (5分钟)
-1 0 1 2 3 4 5
1.
2.
在数轴上表示 解集 规律
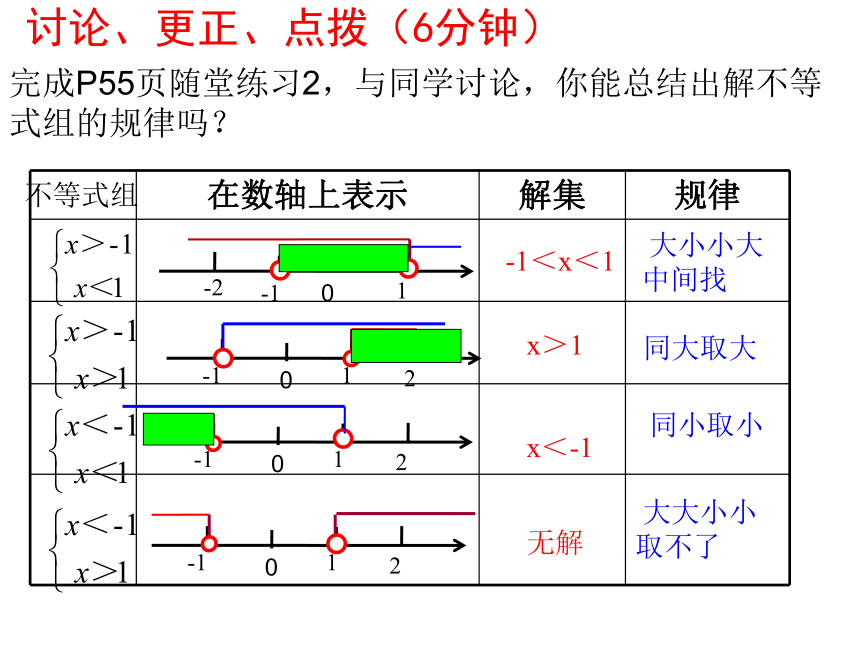
讨论、更正、点拨(6分钟)
完成P55页随堂练习2,与同学讨论,你能总结出解不等式组的规律吗?
1
-1
0
-2
1
-1
0
2
1
-1
0
2
1
-1
0
2
-1<x<1
x>1
x<-1
无解
大小小大中间找
同大取大
同小取小
大大小小取不了
不等式组
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
a
b
a
b
a
b
a
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(设 a<b )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小取不了)
。
。
。
。
。
。
。
。
变式: 不等式组 的解集是_____________
-1< x <2
课堂小结(2分钟)
2.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②找出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一元一次不等式组、解集、解不等式组的概念
一、知识点:
①未知数的个数:1
②未知数的最高次数:1
③左右两边都是整式;
④符号:不等号
二、易错点:
3.一元一次不等式组的解集的规律
大小小大中间找
大大小小取不了(无解)
同小取小
同大取大
1.一元一次不等式组的判定:
2.找各个不等式解集的公共部分
3. 若不等式组 无解,则a的取值范围是( )
当堂训练(15分钟)
1.下列选项中是一元一次不等式组的是( )
A
2. 如图,数轴上所表示的关于x的不等式组的解集是( )
A
A
≤
C
≥
(2)
6.解下列不等式组
(1)
5x-1<3(x+1)
4.不等式组 的解集是x>3,则a的取值范围是_____。
a≤3
5.不等式组 的所有整数解的和为_____。
-2
7.(选做题)
解:解不等式①得 x≥-1
解不等式②得 x>3
在同一条数轴上表示不
等式① ②的解集,如图:
因此,原不等式组的解集为:
① ②
① ②
解:解不等式①得 x≥-1
解不等式②得 x<2
在同一条数轴上表示不
等式① ②的解集,如图:
因此,原不等式组的解集为:
-2 -1 0 1 2
6.解下列不等式组:
(2)
5x-1<3(x+1)
( 1)
x>3
-1≤x<2
-1 0 1 2 3 4 5
7.(选做题)
正本作业 P56知识技能1(1)(3)(6)
2.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②利用数轴求出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一元一次不等式组、解集、解不等式组的概念
一、知识点:
1.未知数的个数:1;
2.未知数的次数:1;
3.左右两边都是整式;
4.符号:不等号
二、易错点:一元一次不等式组的判定:
3.一元一次不等式组的解集的规律
大小小大中间找
大大小小取不了(无解)
同小取小
同大取大
板书设计
2.6.1 一元一次不等式组
解: 解不等式①得
解不等式②得
在同一条数轴上表示不等式① ②的解集,如图:
∴原不等式组的解集为:
x<6
-4
-5
-3
-2
-1
0
1
4
3
2
5
7
6
解不等式组:
①
②
例1:
1、分别求解两个不等式
2、在数轴上表示解集,找出公共部分
3、写出不等式组的解集
2.6.2 一元一次不等式组(2)
第二章 一元一次不等式与一元一次不等式组
课前提问(1分钟)
下列各式中不是一元一次不等式组的是( )
B
学习目标(1分钟)
1、能熟练求出一元一次不等式组的解集并能在数轴
上表示出来。
2、能用不等式组的解集解决简单的实际问题。
自学指导1(1分钟)
学生自学,教师巡视(3分钟)
阅读P57的例2、例3中,注意不等式组的解题的格式,不等式 、 解集的不等号方向相同吗?最终的解集与 、 的解集有何关系?
例2 解不等式组:
例3 解不等式组:
0 1 2 3 4
解:解不等式①得x < 1.5
∴原不等式组的解集为:
在同一条数轴上表示不
等式① ② 的解集如图
x ≥ 4
解:解不等式①得x > 2.5
解不等式②得 x ≥ 4
∴原不等式组的解集为:
在同一条数轴上表示不
等式① ② 的解集如图
2.5
解不等式②得 x <
-2 -1 0 1 2
例2 解不等式组:
例3 解不等式组:
1.5
完成P58页随堂练习第一题(1)(2)
自学检测1(6分钟)
解:解不等式①得
解不等式②得
∴原不等式组无解
① ②
①
②
解:解不等式①得
解不等式②得
∴原不等式组的解集为:
大大小小取不了
同大取大
不等式①②的解集在同一
数轴上表示为:
-1 0 1 2 3
不等式①②的解集在同一
数轴上表示为:
-1 0 1 2 3
讨论、更正、点拨(6分钟)
议一议,是否存在实数x,使得x+3<5,且x-2>4
解:由题意,得
解得:
∴不存在实数x,使得x+3<5,且x-2>4。
(变式):怎样解不等式-5<2x+1<6
解:由题意,得
解得:
∴原不等式的解集为:-3自学指导2(1分钟)
自学课本P59页的“读一读”问题2,思考:
问题2:用若干辆载重量为8t的汽车运一批货物,若每辆汽车只装4t,则剩下20t货物;若每辆汽车装8t,则最后一辆汽车不满也不空,请你算一算:有多少辆汽车运这批货物?
1、设有x辆汽车,则这批货物共有________t。
2、每辆汽车装8t,则(x-1)辆车共装有________t,那么最后一辆汽车装的货物重量为_________________t。
3、根据最后一辆汽车不满也不空,那么可以得出不等式_______________________________.
学生自学,教师巡视(5分钟)
(4x+20)
8(x-1)
[(4x+20)-8(x-1)]
0<(4x+20)-8(x-1)<8
自学检测2(6分钟)
1、 三个数3,1-a,1-2a在数轴上从左到右依次排列,则a的取值范围为_________.
解:依题意得
解得:a<-2
∴a的取值范围是:a<-2
2、 把一堆苹果分给几个小孩,如果每人分3个,则余8个,如果每人分5个,则最后一人得到苹果但不足3个,求小孩的人数和苹果的个数.
解:设有x个小孩,则有苹果(3x+8)个。
依题意得
解得:
∵x为正整数,∴x=6, 3x+8=26
∴有6个小孩,26个苹果。
a<-2
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
a
b
a
b
a
b
a
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(设 a<b )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小取不了)
。
。
。
。
。
。
。
。
变式: 不等式组 的解集是_____________
-1< x <2
2、用不等式组解决实际问题的一般步骤是什么?
①设未知数
②寻找不等关系,列不等式组
③解不等式组
④作答
当堂训练(15分钟)
1、解下列不等式
2、已知不等式组 的解集为-1则(a+1)(b-1)的值为多少?
3、当 x 取哪些整数时,不等式 2(x+2)<x+5 与3(x-2)+8>2x同时成立
解:原不等式组可化为
解不等式①得:x < -10
解不等式②得: x < 2.4
∴原不等式组的解集为:x < -10
在同一条数轴上表示不等式① ② 的解集
-10 2.4
2、已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
解: 由不等式组得:
∵不等式组的解集为: -1< x < 1,
解得: a=1 , b= - 2
∴(a+1)(b-1)=-6
3、当 x 取哪些整数时,不等式 2(x+2)<x+5 与3(x-2)+8>2x同时成立
解: 解2(x+2)<x+5 得x<1
解3(x-2)+8>2x 得x>-2
因为x的取值范围是-2<x<1,且x 取整数,
因此 x= -1, x=0
(正本作业)完成课本P63问题解决15.
5、某社区决定购置一批共享单车.经市场调查得知,购
买3辆男式单车与4辆女式单车费用相同,购买5辆男式
单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需
要22辆,购置两种单车的费用不超过50000元,该社区有几
种购置方案 怎样购置才能使所需总费用最低,最低费用
是多少
(选做题)
5、解:(1)设男式单车x元/辆,女式单车y元/辆,
根据题意,得:
,
答:男式单车2000元/辆,女式单车1500元/辆;
解得:
(2)设购置女式单车m辆,则购置男式单车 (m+4) 辆,
根据题意,得:
解得:
∵m为整数,
∴m的值可以是9、10、11、12,即该社区有四种购置方案;
设购置总费用为W元,
则
∵W随m的增大而增大,
当m=9时,W取得最小值,最小值为39500,
答:该社区共有4种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为39500元.
(选做题)
解:设招聘A种工人x人,则招聘B种工人(150-x)人,依题意得:
150-x≥2x
解得:x≤50
设每月所付的总工资为y元,则 y=1500x+3000(150-x) =450000-1500x
因此当x=50时,所付工资总额最少。
(正本作业)完成课本P63问题解决15.
板书设计
一、解一元一次不等式组的步骤
②利用数轴求出这些不等式解集的公共部分.
①求出这个不等式组中各个不等式的解集.
③表示这个不等式组的解集.
二、一元一次不等式组的解集的规律
大小小大中间找
大大小小取不了(无解)
同小取小
同大取大
2.6.2 一元一次不等式组(2)
2.6.1 一元一次不等式组
第二章 一元一次不等式与一元一次不等式组
课前提问(1分钟)
1.下列不等式中,是一元一次不等式的有( )个.
①x>-3;②xy≥1;③
;④
;⑤
A. 1 B. 2 C. 3 D. 4
B
2.
1
2022/5/4
3
1.理解一元一次不等式组、一元一次不等式组
的解集、解不等式组等概念.
2.会解一元一次不等式组,并会用数轴确定解集.
学习目标 (1分钟)
4、求 ,叫做解不等式组.
2、一元一次不等式组中 ,
就叫做这个一元一次不等式组的解集.
3、不等式组 中,不等式4(x+5)>100的
解集为 ,不等式4(x-5)<68的集解为 .
在同一数轴上可以表示为 不等式组
的解集为 .
阅读课本P54的内容,回答下列问题:
1、一般地,关于 的 合在
一起,就组成一元一次不等式组.
同一未知数
几个一元一次不等式
各个不等式的解集的公共部分
学生自学,教师巡视(3分钟)
x>20
x<22
20< x<22
20
0
22
不等式组解集的过程
自学指导1:(1分钟)
3. 一台装载机每时可装载石料50t,一堆石料的质量在1800t到2200t之间,那么这台装载机大约要用多长时间才能将这堆石料装完,设用x小时可以装完,则_____________________.(只列式)
自学检测1 (5分钟)
1.下列选项中是一元一次不等式组的是( )
D
D
2. 不等式组 的解集在数轴上可表示为( )
易错点:一元一次不等式组的判定:①未知数的个数:1;②未知数的次数:1;③左右两边都是整式;④符号:不等号
1.例1中不等式组的解集与不等式①和不等式②的解集
有何关系?
2.解一元一次不等式组的解题过程分为:
6
自学指导2(1分钟)
阅读例1的解答过程:回答下列问题
学生自学,教师巡视:3分钟
③表示这个不等式组的解集.
②利用数轴求出这些不等式解集的公共部分.
①求出这个不等式组中各个不等式的解集.
解:解不等式①得
解不等式②得
在同一条数轴上表示不
等式① ②的解集,如图:
∴原不等式组的解集为:
① ②
① ②
解:解不等式①得
解不等式②得
在同一条数轴上表示不
等式① ②的解集,如图:
∴原不等式组的解集为:
-2 -1 0 1 2
解下列不等式组:
自学检测2 (5分钟)
-1 0 1 2 3 4 5
1.
2.
在数轴上表示 解集 规律
讨论、更正、点拨(6分钟)
完成P55页随堂练习2,与同学讨论,你能总结出解不等式组的规律吗?
1
-1
0
-2
1
-1
0
2
1
-1
0
2
1
-1
0
2
-1<x<1
x>1
x<-1
无解
大小小大中间找
同大取大
同小取小
大大小小取不了
不等式组
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
a
b
a
b
a
b
a
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(设 a<b )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小取不了)
。
。
。
。
。
。
。
。
变式: 不等式组 的解集是_____________
-1< x <2
课堂小结(2分钟)
2.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②找出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一元一次不等式组、解集、解不等式组的概念
一、知识点:
①未知数的个数:1
②未知数的最高次数:1
③左右两边都是整式;
④符号:不等号
二、易错点:
3.一元一次不等式组的解集的规律
大小小大中间找
大大小小取不了(无解)
同小取小
同大取大
1.一元一次不等式组的判定:
2.找各个不等式解集的公共部分
3. 若不等式组 无解,则a的取值范围是( )
当堂训练(15分钟)
1.下列选项中是一元一次不等式组的是( )
A
2. 如图,数轴上所表示的关于x的不等式组的解集是( )
A
A
≤
C
≥
(2)
6.解下列不等式组
(1)
5x-1<3(x+1)
4.不等式组 的解集是x>3,则a的取值范围是_____。
a≤3
5.不等式组 的所有整数解的和为_____。
-2
7.(选做题)
解:解不等式①得 x≥-1
解不等式②得 x>3
在同一条数轴上表示不
等式① ②的解集,如图:
因此,原不等式组的解集为:
① ②
① ②
解:解不等式①得 x≥-1
解不等式②得 x<2
在同一条数轴上表示不
等式① ②的解集,如图:
因此,原不等式组的解集为:
-2 -1 0 1 2
6.解下列不等式组:
(2)
5x-1<3(x+1)
( 1)
x>3
-1≤x<2
-1 0 1 2 3 4 5
7.(选做题)
正本作业 P56知识技能1(1)(3)(6)
2.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②利用数轴求出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一元一次不等式组、解集、解不等式组的概念
一、知识点:
1.未知数的个数:1;
2.未知数的次数:1;
3.左右两边都是整式;
4.符号:不等号
二、易错点:一元一次不等式组的判定:
3.一元一次不等式组的解集的规律
大小小大中间找
大大小小取不了(无解)
同小取小
同大取大
板书设计
2.6.1 一元一次不等式组
解: 解不等式①得
解不等式②得
在同一条数轴上表示不等式① ②的解集,如图:
∴原不等式组的解集为:
x<6
-4
-5
-3
-2
-1
0
1
4
3
2
5
7
6
解不等式组:
①
②
例1:
1、分别求解两个不等式
2、在数轴上表示解集,找出公共部分
3、写出不等式组的解集
2.6.2 一元一次不等式组(2)
第二章 一元一次不等式与一元一次不等式组
课前提问(1分钟)
下列各式中不是一元一次不等式组的是( )
B
学习目标(1分钟)
1、能熟练求出一元一次不等式组的解集并能在数轴
上表示出来。
2、能用不等式组的解集解决简单的实际问题。
自学指导1(1分钟)
学生自学,教师巡视(3分钟)
阅读P57的例2、例3中,注意不等式组的解题的格式,不等式 、 解集的不等号方向相同吗?最终的解集与 、 的解集有何关系?
例2 解不等式组:
例3 解不等式组:
0 1 2 3 4
解:解不等式①得x < 1.5
∴原不等式组的解集为:
在同一条数轴上表示不
等式① ② 的解集如图
x ≥ 4
解:解不等式①得x > 2.5
解不等式②得 x ≥ 4
∴原不等式组的解集为:
在同一条数轴上表示不
等式① ② 的解集如图
2.5
解不等式②得 x <
-2 -1 0 1 2
例2 解不等式组:
例3 解不等式组:
1.5
完成P58页随堂练习第一题(1)(2)
自学检测1(6分钟)
解:解不等式①得
解不等式②得
∴原不等式组无解
① ②
①
②
解:解不等式①得
解不等式②得
∴原不等式组的解集为:
大大小小取不了
同大取大
不等式①②的解集在同一
数轴上表示为:
-1 0 1 2 3
不等式①②的解集在同一
数轴上表示为:
-1 0 1 2 3
讨论、更正、点拨(6分钟)
议一议,是否存在实数x,使得x+3<5,且x-2>4
解:由题意,得
解得:
∴不存在实数x,使得x+3<5,且x-2>4。
(变式):怎样解不等式-5<2x+1<6
解:由题意,得
解得:
∴原不等式的解集为:-3
自学课本P59页的“读一读”问题2,思考:
问题2:用若干辆载重量为8t的汽车运一批货物,若每辆汽车只装4t,则剩下20t货物;若每辆汽车装8t,则最后一辆汽车不满也不空,请你算一算:有多少辆汽车运这批货物?
1、设有x辆汽车,则这批货物共有________t。
2、每辆汽车装8t,则(x-1)辆车共装有________t,那么最后一辆汽车装的货物重量为_________________t。
3、根据最后一辆汽车不满也不空,那么可以得出不等式_______________________________.
学生自学,教师巡视(5分钟)
(4x+20)
8(x-1)
[(4x+20)-8(x-1)]
0<(4x+20)-8(x-1)<8
自学检测2(6分钟)
1、 三个数3,1-a,1-2a在数轴上从左到右依次排列,则a的取值范围为_________.
解:依题意得
解得:a<-2
∴a的取值范围是:a<-2
2、 把一堆苹果分给几个小孩,如果每人分3个,则余8个,如果每人分5个,则最后一人得到苹果但不足3个,求小孩的人数和苹果的个数.
解:设有x个小孩,则有苹果(3x+8)个。
依题意得
解得:
∵x为正整数,∴x=6, 3x+8=26
∴有6个小孩,26个苹果。
a<-2
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
a
b
a
b
a
b
a
b
解集为 : x> b
(同大取大)
解集为 : x<a
(同小取小)
一元一次不等式组的解集的规律图析
(设 a<b )
解集为: a<x<b
(大小小大中间找)
解集为:无解
(大大小小取不了)
。
。
。
。
。
。
。
。
变式: 不等式组 的解集是_____________
-1< x <2
2、用不等式组解决实际问题的一般步骤是什么?
①设未知数
②寻找不等关系,列不等式组
③解不等式组
④作答
当堂训练(15分钟)
1、解下列不等式
2、已知不等式组 的解集为-1
3、当 x 取哪些整数时,不等式 2(x+2)<x+5 与3(x-2)+8>2x同时成立
解:原不等式组可化为
解不等式①得:x < -10
解不等式②得: x < 2.4
∴原不等式组的解集为:x < -10
在同一条数轴上表示不等式① ② 的解集
-10 2.4
2、已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
解: 由不等式组得:
∵不等式组的解集为: -1< x < 1,
解得: a=1 , b= - 2
∴(a+1)(b-1)=-6
3、当 x 取哪些整数时,不等式 2(x+2)<x+5 与3(x-2)+8>2x同时成立
解: 解2(x+2)<x+5 得x<1
解3(x-2)+8>2x 得x>-2
因为x的取值范围是-2<x<1,且x 取整数,
因此 x= -1, x=0
(正本作业)完成课本P63问题解决15.
5、某社区决定购置一批共享单车.经市场调查得知,购
买3辆男式单车与4辆女式单车费用相同,购买5辆男式
单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需
要22辆,购置两种单车的费用不超过50000元,该社区有几
种购置方案 怎样购置才能使所需总费用最低,最低费用
是多少
(选做题)
5、解:(1)设男式单车x元/辆,女式单车y元/辆,
根据题意,得:
,
答:男式单车2000元/辆,女式单车1500元/辆;
解得:
(2)设购置女式单车m辆,则购置男式单车 (m+4) 辆,
根据题意,得:
解得:
∵m为整数,
∴m的值可以是9、10、11、12,即该社区有四种购置方案;
设购置总费用为W元,
则
∵W随m的增大而增大,
当m=9时,W取得最小值,最小值为39500,
答:该社区共有4种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为39500元.
(选做题)
解:设招聘A种工人x人,则招聘B种工人(150-x)人,依题意得:
150-x≥2x
解得:x≤50
设每月所付的总工资为y元,则 y=1500x+3000(150-x) =450000-1500x
因此当x=50时,所付工资总额最少。
(正本作业)完成课本P63问题解决15.
板书设计
一、解一元一次不等式组的步骤
②利用数轴求出这些不等式解集的公共部分.
①求出这个不等式组中各个不等式的解集.
③表示这个不等式组的解集.
二、一元一次不等式组的解集的规律
大小小大中间找
大大小小取不了(无解)
同小取小
同大取大
2.6.2 一元一次不等式组(2)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
