沪科版七年级数学下册 10.2平行线的判定(第4课时)课件(共23张PPT)
文档属性
| 名称 | 沪科版七年级数学下册 10.2平行线的判定(第4课时)课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 330.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 09:51:41 | ||
图片预览



文档简介
(共23张PPT)
沪科版七年级下册
10.2 平行线的判定
平行线的判定方法练习
第四课时
学习目标
2、 掌握垂直于同一条直线的两条直线互相平行.
3、 经历例题的分析过程,从中体会转化的思想和
分析问题的方法,进一步培养推理能力.
1、进一步理解掌握平行线的判定定理,能熟练运用平行线的判定定理判定两条直线是否平行
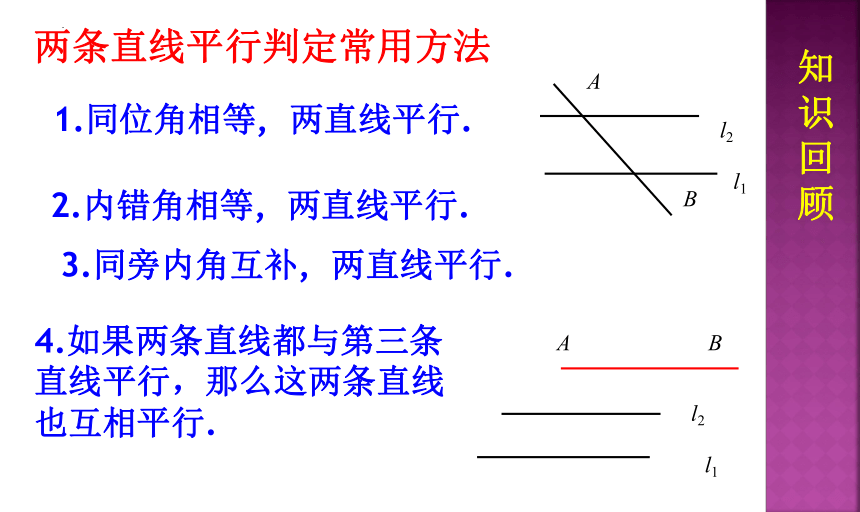
两条直线平行判定常用方法
知识回顾
l2
l1
A
B
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
l2
l1
A
B
4.如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
A
B
C
D
E
1
2
3
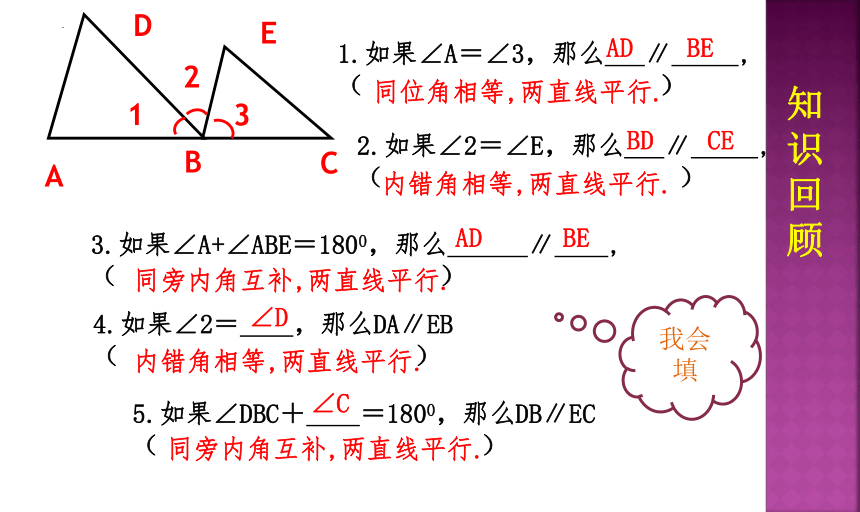
知识回顾
1.如果∠A=∠3,那么 ∥ ,
( )
AD BE
同位角相等,两直线平行.
2.如果∠2=∠E,那么 ∥ ,
( )
BD CE
内错角相等,两直线平行.
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
AD BE
同旁内角互补,两直线平行.
4.如果∠2= ,那么DA∥EB
( )
∠D
内错角相等,两直线平行.
5.如果∠DBC+ =1800,那么DB∥EC
( )
∠C
同旁内角互补,两直线平行.
我会填
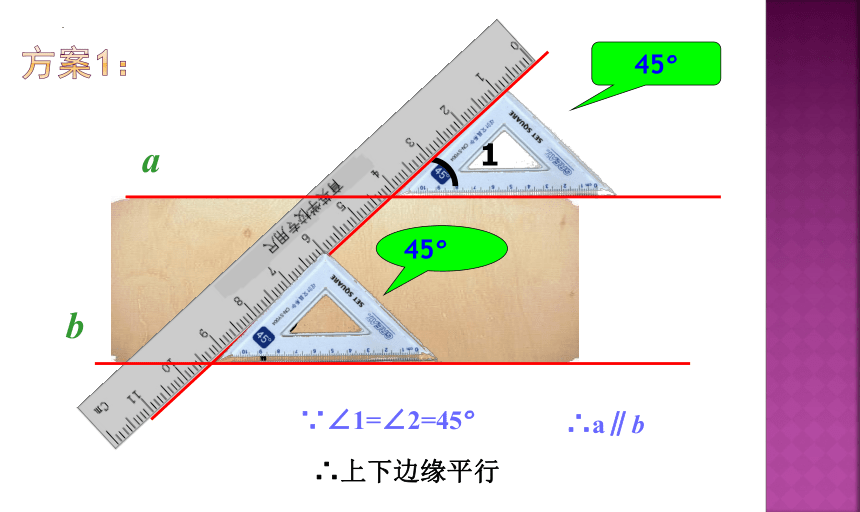
有一块木板,身边只有直尺和三角尺,我们怎样才能知道它上下边缘是否平行?
试一试
知识深入
方案1:
1
2
45°
45°
∵∠1=∠2=45°
∴上下边缘平行
a
b
∴a∥b
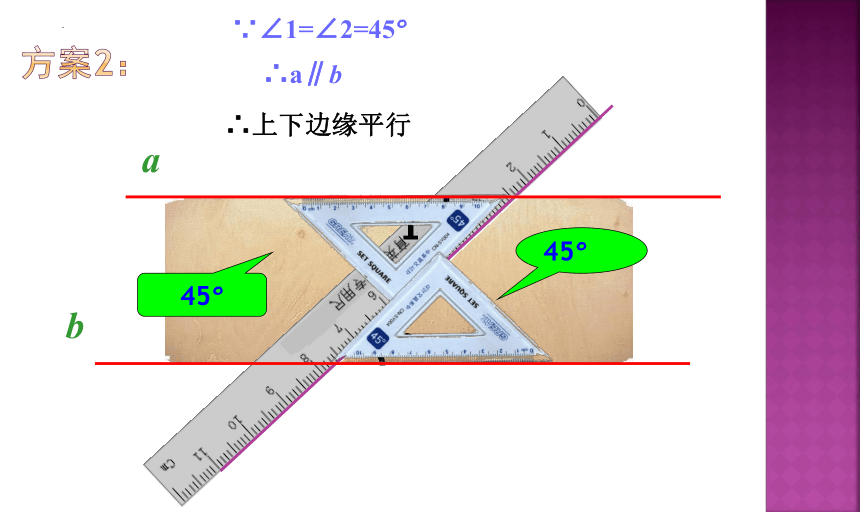
方案2:
45°
1
2
45°
∵∠1=∠2=45°
∴上下边缘平行
a
b
∴a∥b
试一试
┓
┓
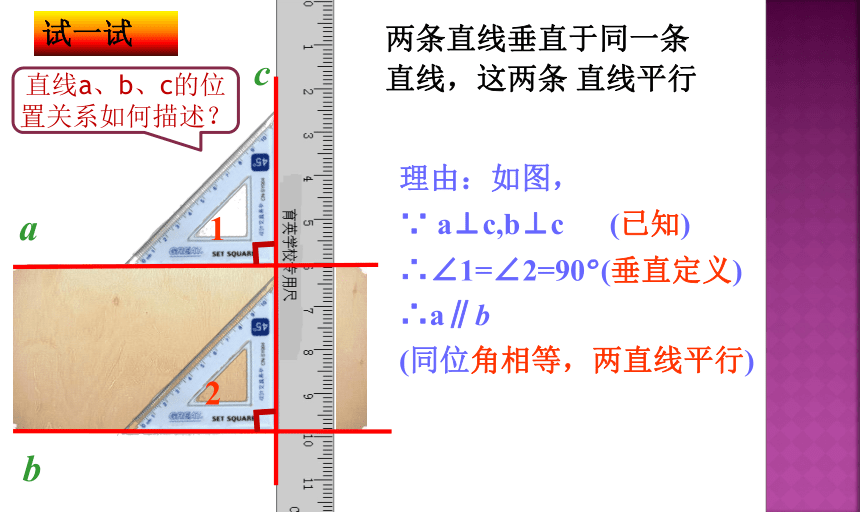
两条直线垂直于同一条直线,这两条 直线平行
a
b
c
直线a、b、c的位置关系如何描述?
理由:如图,
∵ a⊥c,b⊥c (已知)
∴∠1=∠2=90°(垂直定义)
∴a∥b
(同位角相等,两直线平行)
1
2
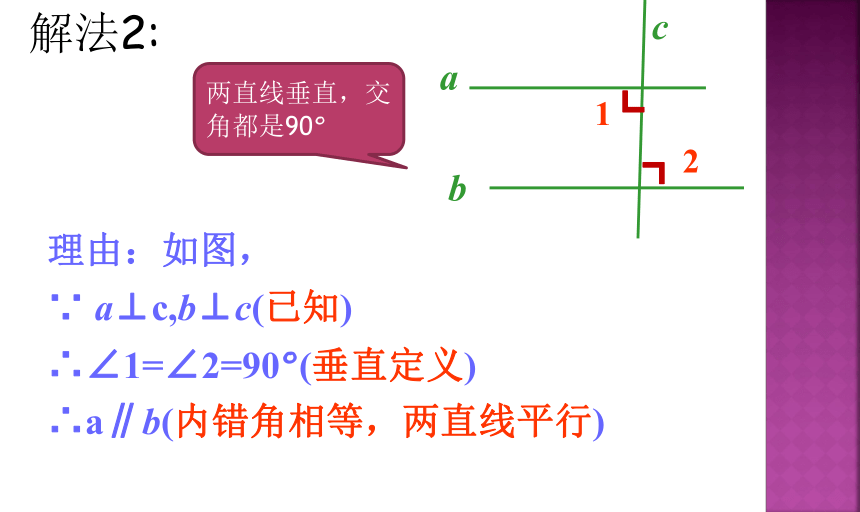
理由:如图,
∵ a⊥c,b⊥c(已知)
∴∠1=∠2=90°(垂直定义)
∴a∥b(内错角相等,两直线平行)
a
b
c
1
2
解法2:
┓
┓
两直线垂直,交角都是90°
a
b
c
1
2
解法3:
┓
┓
理由:如图,
∵ a⊥ c, b⊥c (已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴a∥b(同旁内角互补,两直线平行)
两直线垂直,交角都是90°
如果两条直线都垂直于同一条直线,那么这两条直线平行。
b
c
1
2
a
几何语言
垂直于同一条直线的两条直线平行.
简说为:
结论
∵ b⊥a,c⊥a
∴b∥c
例1:如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°, ∠ABG=30°。请判断AE与CD是否平行,并说明理由。
例题讲解
A
B
C
D
E
F
G
60°
30°
解:AE与CD平行。理由如下:
∵AB⊥CD于点B(已知)
∴∠ABD=90°(垂直定义)
∵∠ABG=30°(已知)
∴∠FBD= ∠ABD -∠ABG
=90°30°=60°
∵∠FGE=60°(已知)
∴∠FGE=∠FBD=60°(等量代换)
∴AE∥CD
(同位角相等,两直线平行)
例2、如图,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,试说明BF∥CE
A
B
C
D
E
F
2
1
证明:
∵AB⊥ BC,BC⊥CD(已知)
∴∠ABC=∠BCD=90°(垂直定义)
∵∠1=∠2
∴∠ABC-∠1=∠BCD-∠2
∴∠EBC=∠BCF
∴BF∥CE(内错角相等,两直线平行)
例题讲解
例3、如图, 若 ∠EFD=110°,∠FED=35°,ED 平分∠BEF,那么AB与CD平行吗? 请说明你的理由.
解:AB与CD平行. 理由如下:
∵ED平分∠BEF,∠FED=35°(已知),
∴∠BEF=2∠FED=70°(角平分线的性质).
∵∠EFD=110°(已知)
∴∠BEF+∠EFD=70°+110°=180°
∴AB∥CD(同旁内角互补,两直线平行).
A
B
C
D
E
F
例题讲解
知识巩固
1、完成下列填空
(1).如图
∵∠1=∠2(已知)
∴____∥_____( )
∵∠2=∠3,(已知)
∴____∥____( )
A
B
C
D
E
F
2
1
AB
3
ED
BC
EF
同位角相等,两直线平行
(2)、如图
∵∠1=∠2(已知)
∴____∥____( )
∵∠3=∠4(已知)
∴____∥____( )
同位角相等,两直线平行
A
B
C
D
2
1
3
4
AD
BC
AB
CD
内错角相等,两直线平行
内错角相等,两直线平行
(3)如图,已知∠1=30°,∠2或 ∠3满足条件
,则a//b
2
1
3
a
b
c
∠2=150或∠3=30°
(4).直线ab被直线c所截,给出下列条件:
(1)∠1=∠2; (2)∠3=∠6;
(3)∠4=∠1; (4)∠6+∠7=180°.
其中能识别a∥b的条件序号是 .
4
8
6
2
1
5
3
7
a
b
c
(1)(2)(4)
知识巩固
(1)如图:可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
C
2、选一选
知识巩固
1
2
3
A
E
B
C
D
(2)如图,给出下面的推理,其中正确的是( )
①因为∠B=∠BEF,所以AB∥EF;
②因为∠B=∠CDE,所以AB∥CD;
③因为∠B+∠BEC=180°,所以AB∥EF;
④因为AB∥CD,CD∥EF,所以AB∥EF.
A.①②③ B.①②④ C.①③④ D.②③④
B
A
B
C
D
E
F
(3)、如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠4,则b∥c
D.若∠3+∠5=180°,则a∥c
C
a
c
b
d
e
2
3
4
5
1
(4)下列说法错误的是( )
A.同位角不一定相等 B.对顶角都相等
C.同旁内角互补 D.同位角相等,两直线平行。
C
知识巩固
(5)、如图所示,工程技术人员常用一种绘图工具丁字尺画平行线
方法是:用丁字尺画物体边缘的两条垂线,这样画的理由有下列4种说法,其中正确的是( )
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行;
④平面内垂直于同一直线的
两条直线平行.
A. ①②③ B. ①②④
C. ①③④ D.①③
C
知识巩固
(6)、一辆汽车在公路上行驶,两次拐弯后,仍然在原来的方向上平行行驶,那么两个拐弯的角度可能为( )
A、先向右拐50°,再向左拐50°
B、先向右拐50°,再向右拐50°
C、先向右拐50°,再向右拐130°
D、先向右拐50°,再向左拐130°
A
知识巩固
(1)如图,已知BE、EC分别平分∠ABC,∠BCD,且∠1与∠2互余,试说明AB∥DC.
∵BE,EC分别平分∠ABC,∠BCD(已知),
∴∠ABC=2∠1,∠BCD=2∠2(角平分线的性质).
∴∠ABC+∠BCD=2∠1+2∠2=2(∠1+∠2)=180°.
∴AB∥DC(同旁内角互补,两直线平行).
3、试说明理由
A
B
C
D
E
2
1
解:
∵∠1与∠2互余,
∴∠1+∠2=90°.
知识巩固
∵ ∠1=∠B (已知),
∴ MN∥BC (内错角相等,两直线平行).
∵ ∠2=∠C (已知),
∴ EF∥BC (同位角相等,两直线平行).
∴ MN∥EF ( ).
证明:
F
E
M
A
2
1
B
C
(2)已知:如图,∠1=∠B,∠2=∠C,
求证:MN∥EF.
N
平行于同一直线的两条直线平行
知识巩固
归纳小结
判定两条直线平行的方法:
同位角相等,两直线平行
平行线判定1:
内错角相等,两直线平行
平行线判定2:
同旁内角互补,两直线平行
平行线判定3:
若a∥b,b∥c,则a∥c(平行公理的推论)
平行线判定4:
在同一平面内,若a⊥b,b⊥c,则a∥c
平行线判定5:
沪科版七年级下册
10.2 平行线的判定
平行线的判定方法练习
第四课时
学习目标
2、 掌握垂直于同一条直线的两条直线互相平行.
3、 经历例题的分析过程,从中体会转化的思想和
分析问题的方法,进一步培养推理能力.
1、进一步理解掌握平行线的判定定理,能熟练运用平行线的判定定理判定两条直线是否平行
两条直线平行判定常用方法
知识回顾
l2
l1
A
B
1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
l2
l1
A
B
4.如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
A
B
C
D
E
1
2
3
知识回顾
1.如果∠A=∠3,那么 ∥ ,
( )
AD BE
同位角相等,两直线平行.
2.如果∠2=∠E,那么 ∥ ,
( )
BD CE
内错角相等,两直线平行.
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
AD BE
同旁内角互补,两直线平行.
4.如果∠2= ,那么DA∥EB
( )
∠D
内错角相等,两直线平行.
5.如果∠DBC+ =1800,那么DB∥EC
( )
∠C
同旁内角互补,两直线平行.
我会填
有一块木板,身边只有直尺和三角尺,我们怎样才能知道它上下边缘是否平行?
试一试
知识深入
方案1:
1
2
45°
45°
∵∠1=∠2=45°
∴上下边缘平行
a
b
∴a∥b
方案2:
45°
1
2
45°
∵∠1=∠2=45°
∴上下边缘平行
a
b
∴a∥b
试一试
┓
┓
两条直线垂直于同一条直线,这两条 直线平行
a
b
c
直线a、b、c的位置关系如何描述?
理由:如图,
∵ a⊥c,b⊥c (已知)
∴∠1=∠2=90°(垂直定义)
∴a∥b
(同位角相等,两直线平行)
1
2
理由:如图,
∵ a⊥c,b⊥c(已知)
∴∠1=∠2=90°(垂直定义)
∴a∥b(内错角相等,两直线平行)
a
b
c
1
2
解法2:
┓
┓
两直线垂直,交角都是90°
a
b
c
1
2
解法3:
┓
┓
理由:如图,
∵ a⊥ c, b⊥c (已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴a∥b(同旁内角互补,两直线平行)
两直线垂直,交角都是90°
如果两条直线都垂直于同一条直线,那么这两条直线平行。
b
c
1
2
a
几何语言
垂直于同一条直线的两条直线平行.
简说为:
结论
∵ b⊥a,c⊥a
∴b∥c
例1:如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°, ∠ABG=30°。请判断AE与CD是否平行,并说明理由。
例题讲解
A
B
C
D
E
F
G
60°
30°
解:AE与CD平行。理由如下:
∵AB⊥CD于点B(已知)
∴∠ABD=90°(垂直定义)
∵∠ABG=30°(已知)
∴∠FBD= ∠ABD -∠ABG
=90°30°=60°
∵∠FGE=60°(已知)
∴∠FGE=∠FBD=60°(等量代换)
∴AE∥CD
(同位角相等,两直线平行)
例2、如图,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,试说明BF∥CE
A
B
C
D
E
F
2
1
证明:
∵AB⊥ BC,BC⊥CD(已知)
∴∠ABC=∠BCD=90°(垂直定义)
∵∠1=∠2
∴∠ABC-∠1=∠BCD-∠2
∴∠EBC=∠BCF
∴BF∥CE(内错角相等,两直线平行)
例题讲解
例3、如图, 若 ∠EFD=110°,∠FED=35°,ED 平分∠BEF,那么AB与CD平行吗? 请说明你的理由.
解:AB与CD平行. 理由如下:
∵ED平分∠BEF,∠FED=35°(已知),
∴∠BEF=2∠FED=70°(角平分线的性质).
∵∠EFD=110°(已知)
∴∠BEF+∠EFD=70°+110°=180°
∴AB∥CD(同旁内角互补,两直线平行).
A
B
C
D
E
F
例题讲解
知识巩固
1、完成下列填空
(1).如图
∵∠1=∠2(已知)
∴____∥_____( )
∵∠2=∠3,(已知)
∴____∥____( )
A
B
C
D
E
F
2
1
AB
3
ED
BC
EF
同位角相等,两直线平行
(2)、如图
∵∠1=∠2(已知)
∴____∥____( )
∵∠3=∠4(已知)
∴____∥____( )
同位角相等,两直线平行
A
B
C
D
2
1
3
4
AD
BC
AB
CD
内错角相等,两直线平行
内错角相等,两直线平行
(3)如图,已知∠1=30°,∠2或 ∠3满足条件
,则a//b
2
1
3
a
b
c
∠2=150或∠3=30°
(4).直线ab被直线c所截,给出下列条件:
(1)∠1=∠2; (2)∠3=∠6;
(3)∠4=∠1; (4)∠6+∠7=180°.
其中能识别a∥b的条件序号是 .
4
8
6
2
1
5
3
7
a
b
c
(1)(2)(4)
知识巩固
(1)如图:可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
C
2、选一选
知识巩固
1
2
3
A
E
B
C
D
(2)如图,给出下面的推理,其中正确的是( )
①因为∠B=∠BEF,所以AB∥EF;
②因为∠B=∠CDE,所以AB∥CD;
③因为∠B+∠BEC=180°,所以AB∥EF;
④因为AB∥CD,CD∥EF,所以AB∥EF.
A.①②③ B.①②④ C.①③④ D.②③④
B
A
B
C
D
E
F
(3)、如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠4,则b∥c
D.若∠3+∠5=180°,则a∥c
C
a
c
b
d
e
2
3
4
5
1
(4)下列说法错误的是( )
A.同位角不一定相等 B.对顶角都相等
C.同旁内角互补 D.同位角相等,两直线平行。
C
知识巩固
(5)、如图所示,工程技术人员常用一种绘图工具丁字尺画平行线
方法是:用丁字尺画物体边缘的两条垂线,这样画的理由有下列4种说法,其中正确的是( )
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行;
④平面内垂直于同一直线的
两条直线平行.
A. ①②③ B. ①②④
C. ①③④ D.①③
C
知识巩固
(6)、一辆汽车在公路上行驶,两次拐弯后,仍然在原来的方向上平行行驶,那么两个拐弯的角度可能为( )
A、先向右拐50°,再向左拐50°
B、先向右拐50°,再向右拐50°
C、先向右拐50°,再向右拐130°
D、先向右拐50°,再向左拐130°
A
知识巩固
(1)如图,已知BE、EC分别平分∠ABC,∠BCD,且∠1与∠2互余,试说明AB∥DC.
∵BE,EC分别平分∠ABC,∠BCD(已知),
∴∠ABC=2∠1,∠BCD=2∠2(角平分线的性质).
∴∠ABC+∠BCD=2∠1+2∠2=2(∠1+∠2)=180°.
∴AB∥DC(同旁内角互补,两直线平行).
3、试说明理由
A
B
C
D
E
2
1
解:
∵∠1与∠2互余,
∴∠1+∠2=90°.
知识巩固
∵ ∠1=∠B (已知),
∴ MN∥BC (内错角相等,两直线平行).
∵ ∠2=∠C (已知),
∴ EF∥BC (同位角相等,两直线平行).
∴ MN∥EF ( ).
证明:
F
E
M
A
2
1
B
C
(2)已知:如图,∠1=∠B,∠2=∠C,
求证:MN∥EF.
N
平行于同一直线的两条直线平行
知识巩固
归纳小结
判定两条直线平行的方法:
同位角相等,两直线平行
平行线判定1:
内错角相等,两直线平行
平行线判定2:
同旁内角互补,两直线平行
平行线判定3:
若a∥b,b∥c,则a∥c(平行公理的推论)
平行线判定4:
在同一平面内,若a⊥b,b⊥c,则a∥c
平行线判定5:
