人教版 八年级下册19.2.2一次函数的平移变换规律 课件(共29张PPT)
文档属性
| 名称 | 人教版 八年级下册19.2.2一次函数的平移变换规律 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 09:57:56 | ||
图片预览




文档简介
(共29张PPT)
19.2 一次函数
第十九章 一次函数
19.2.2 一次函数
第5课时
一、一次函数的平移变换规律
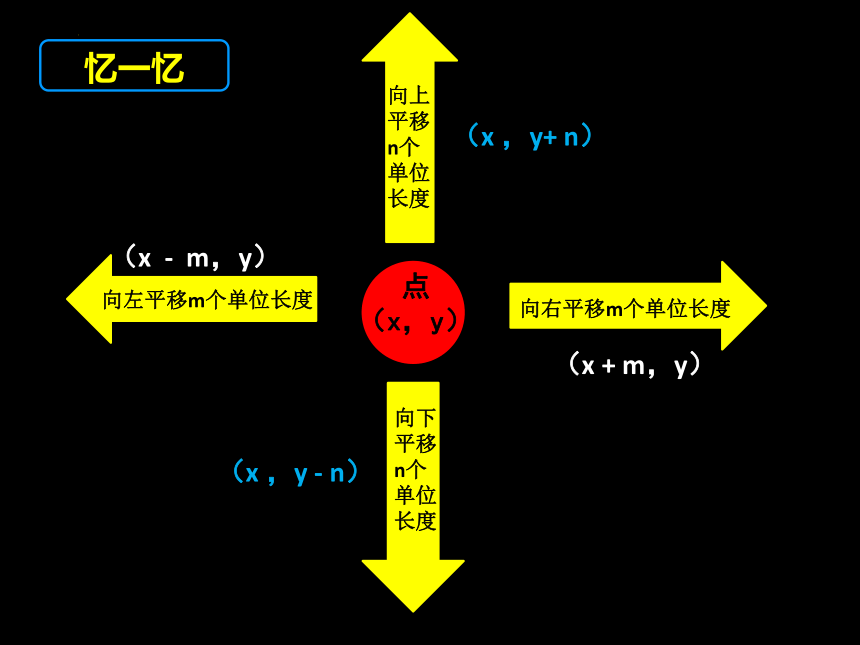
忆一忆
点
(x,y)
向右平移m个单位长度
(x + m,y)
向左平移m个单位长度
(x - m,y)
向下平移
n个
单位长度
向上平移
n个
单位长度
(x ,y+ n)
(x ,y - n)
一次函数的图象(直线)如何平移呢?
我们知道,图形在平移时,图形上的每一个点都作了相同的变换,所以研究一次函数的平移,我们只需抓住点的平移.
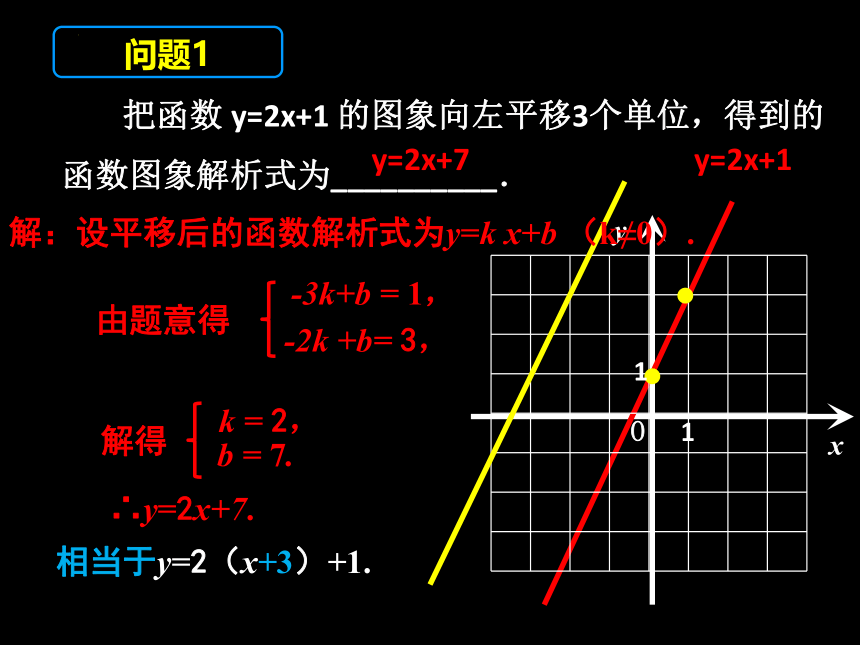
把函数 y=2x+1 的图象向左平移3个单位,得到的
函数图象解析式为__________.
y=2x+7
O
x
y
y=2x+1
问题1
解:设平移后的函数解析式为y=k x+b (k≠0).
-3k+b = 1,
由题意得
b = 7.
解得
∴y=2x+7.
-2k +b= 3,
k = 2,
相当于y=2(x+3)+1.
1
1
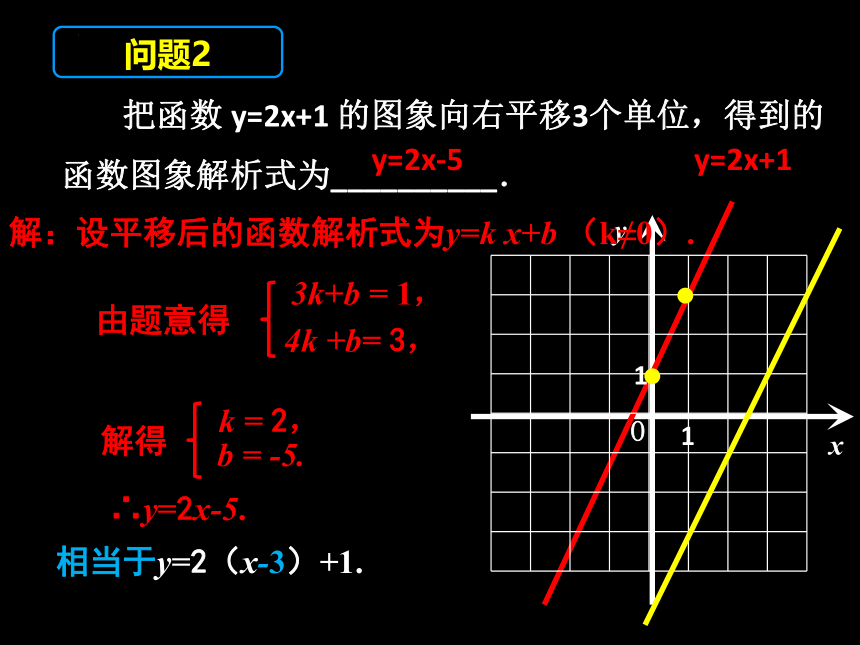
把函数 y=2x+1 的图象向右平移3个单位,得到的
函数图象解析式为__________.
y=2x-5
O
x
y
y=2x+1
问题2
解:设平移后的函数解析式为y=k x+b (k≠0).
3k+b = 1,
由题意得
b = -5.
解得
∴y=2x-5.
4k +b= 3,
k = 2,
相当于y=2(x-3)+1.
1
1
一次函数图象左右平移规律
(1)若把直线y=k x+b (k≠0)沿x轴向左平移m个单位
长度,则平移后的函数解析式为 .
y=k(x+m) +b
(2)若把直线y=k x+b (k≠0)沿x轴向右平移m个单位
长度,则平移后的函数解析式为 .
y=k(x-m) +b
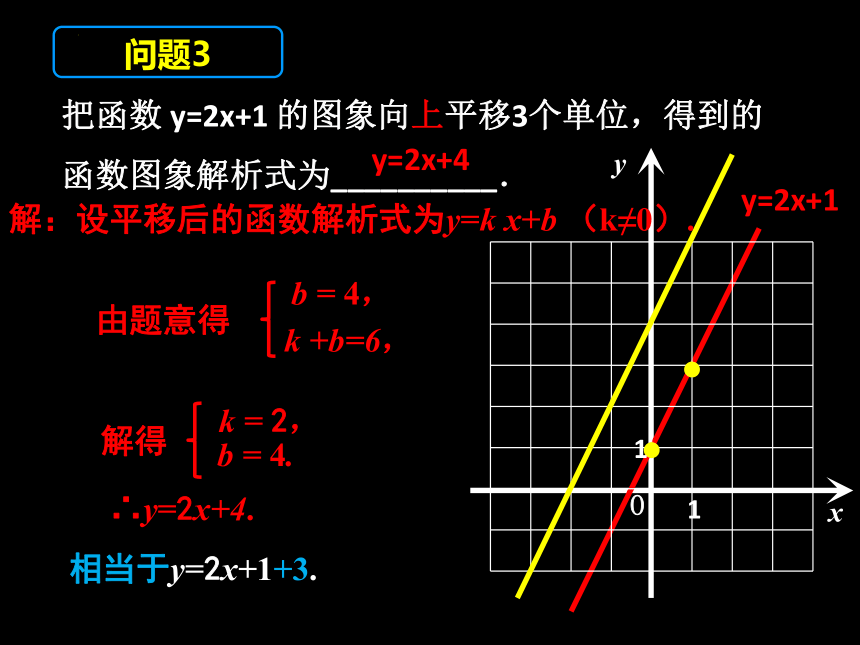
把函数 y=2x+1 的图象向上平移3个单位,得到的
函数图象解析式为__________.
y=2x+4
O
x
y
y=2x+1
问题3
解:设平移后的函数解析式为y=k x+b (k≠0).
b = 4,
由题意得
b = 4.
解得
∴y=2x+4.
k +b=6,
k = 2,
相当于y=2x+1+3.
1
1
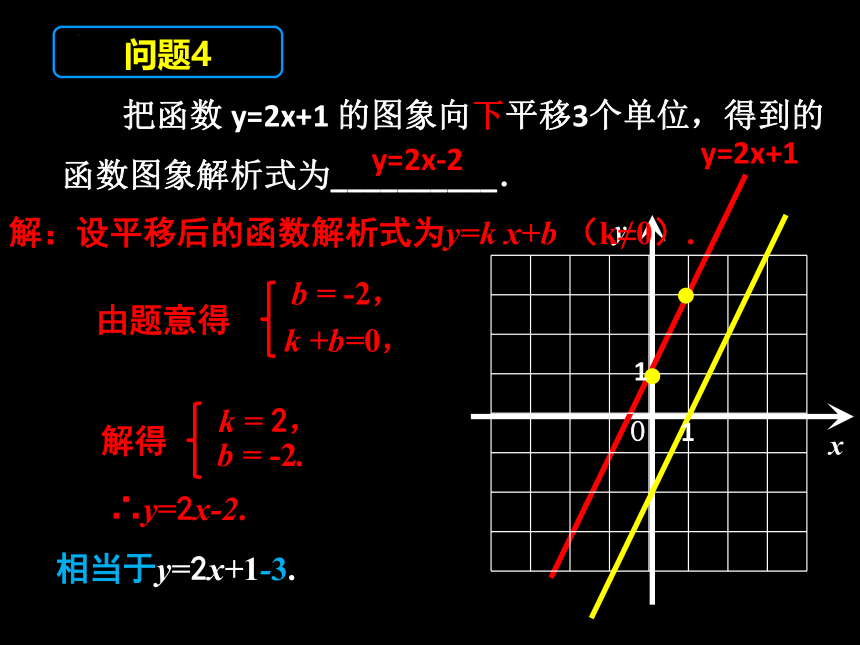
把函数 y=2x+1 的图象向下平移3个单位,得到的
函数图象解析式为__________.
y=2x-2
O
x
y
y=2x+1
问题4
解:设平移后的函数解析式为y=k x+b (k≠0).
b = -2,
由题意得
b = -2.
解得
∴y=2x-2.
k +b=0,
k = 2,
相当于y=2x+1-3.
1
1
一次函数图象上下平移规律
(1)若把直线y=k x+b (k≠0)沿y轴向上平移n个单位
长度,则平移后的函数解析式为 .
y=k x+b +n
(2)若把直线y=k x+b (k≠0)沿y轴向下平移n个单位
长度,则平移后的函数解析式为 .
y=k x+b -n
换个角度去观察和思考,会
不会产生不同的效果,有别样的收获呢?
把函数 y=2x+1 的图象向左平移3个单位,得到的
函数图象解析式为__________.
y=2x+7
O
x
y
y=2x+1
问题1
也可以看作是向上
平移6个单位长度.
y=2x+1+6.
1
1
把函数 y=2x+1 的图象向右平移3个单位,得到的
函数图象解析式为__________.
y=2x-5
O
x
y
y=2x+1
问题2
下
6
也可以看作是向 平移 个单位长度.
y=2x+1-6.
1
1
把函数 y=2x+1 的图象向上平移3个单位,得到的
函数图象解析式为__________.
y=2x+4
O
x
y
y=2x+1
问题3
左
1.5
也可以看作是向 平移 个单位长度.
y=2(x+1.5)+1.
1
1
把函数 y=2x+1 的图象向下平移3个单位,得到的
函数图象解析式为__________.
y=2x-2
O
x
y
y=2x+1
问题4
右
1.5
也可以看作是向 平移 个单位长度.
y=2(x-1.5)+1.
1
1
平移口诀
左加右减自变量,上加下减常数项.
平移规律
(2)向上平移b + n,向下平移b-n.(改变b值)
(1)向左平移k(x + m),向右平移k(x - m) . (改变x值)
(3)平移前后的两个图象既可以上下平移得到,
也可以左右平移得到.
(4)平移不改变倾斜程度,所以不影响k值,
平移前后的两直线平行.
二、一次函数的平移规律在求函数表达式中的应用
例 写出将直线y=3x-2分别进行上、下、左、右平
移5个单位长度后的解析式.
解:
向上
y=3x-2+5
即y=3x+3
向下
y=3x-2-5
即y=3x-7
向左
y=3(x+5)-2
即y=3x+13
向右
y=3(x-5)-2
即y=3x-17
即时小练
1.在平面直角坐标系中,将直线l1: y=-3x-2 沿x轴
向左平移1个单位长度,再向上平移3个单位长度,
得到一条新的直线l2 ,则该直线l2的表达式为( )
A. y=-3x-9 B. y=-3x-2
C. y=-3x+2 D. y=-3x+9
y=-3(x+1)-2 +3
即y=-3x-2
B
A
2. 在平面直角坐标系中,将直线y=2x+1沿y轴向下平
移5个单位后,得到一条新的直线,该直线与x轴
的交点坐标是( )
A.(2,0) B.(-2,0)
C.(0,1) D.(0,-4)
3. 在平面直角坐标系中,将直线l1: y=-2x-2 平移
后,得到直线l2: y=-2x+4 ,则下列平移方法正
确的是( )
A.将l1向右平移4个单位长度
B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度
D.将l1向右平移3个单位长度
y=-2(x-4)-2
y=-2(x-6)-2
y=-2x-2+2
y=-2(x-3)-2
D
4. 在平面直角坐标系中,将直线y=kx-6 沿x轴向左
平移3个单位长度后恰好经过原点,则k的值为( )
A.-2 B.2
C.-3 D.3
y=k(x+3)-6
即y=kx+3k-6
把(0,0)代入y=kx+3k-6 中,
或3k-6 =0,
解得k=2.
B
5. 在平面直角坐标系中,将直线y=2x+m-1 沿x轴向左
平移3个单位长度后,得到一个正比例函数的图象,
则m的值为( )
A.-5 B.5
C.-6 D.6
y=2(x+3)+ m-1
即y=2x+ m+5
把(0,0)代入y=2x+m+5 中,
或m+5 =0,
解得m=-5.
A
6. 已知正比例函数y=kx(k ≠ 0)的图象过点(2,3),
把正比例函数y=kx (k ≠ 0)的图象平移,使它
过点(1,-1),则平移后的函数图象大致是( )
O
x
y
1
-1
O
x
y
1
-1
O
x
y
1
-1
-2
O
x
y
1
-1
-2
A. B. C. D.
D
K=1.5
y=1.5X+b
b=-2.5
与y轴交于(0,-2.5)
把(1,-1)代入得
y=1.5X-2.5
7. 如图,一次函数y=(m-3)x-m+1 的图象分别与x
轴、y轴的负半轴相交于A、B.
(2)若该一次函数向上平移1个单位长度就通过原
点,求m的值.
(1)求m的取值范围;
O
x
y
A
B
解:(1)
m-3 ﹤ 0,
由题意得
1﹤m﹤3.
解得
-m+1﹤ 0,
(2)平移后的解析式为 y=(m-3)x-m+2.
∵平移后过原点,
∴-m+2=0,
解得m=2.
素养提升
在平面直角坐标系中,一次函数y=kx+b (k≠0)的图 象由函数
y=0.5x的图象向下平移1个单位长度得到.
(1)求这个一次函数的解析式;
解:(1)
由题意知这个一次函数的解析式为y=0.5x-1.
(2)当x﹥-2时,对于x的每一个值,函数y=mx(m≠0)的值大于
一次函数y=kx+b (k≠0)的值,直接写出m的取值范围.
O
x
y
y=0.5x-1
m=1
(-2,-2)
m=0.5
m ﹤ 0.5
(2)0.5 ≤ m ≤ 1
m ﹥ 1
y=mx
( )
( )
( )
( )
( )
1
1
向右平移m个单位长度
Y=k(x – m)+b
向左平移m个单位长度
向下平移
n个
单位长度
向上平移
n个
单位长度
y=kx+b+ n
课堂小结
一次函数图象y=kx+b(k≠0)
y=kx+b- n
Y=k(x +m)+b
二次函数也是一样的原理.
用脑思考,
用心琢磨,
用行动证实.
19.2 一次函数
第十九章 一次函数
19.2.2 一次函数
第5课时
一、一次函数的平移变换规律
忆一忆
点
(x,y)
向右平移m个单位长度
(x + m,y)
向左平移m个单位长度
(x - m,y)
向下平移
n个
单位长度
向上平移
n个
单位长度
(x ,y+ n)
(x ,y - n)
一次函数的图象(直线)如何平移呢?
我们知道,图形在平移时,图形上的每一个点都作了相同的变换,所以研究一次函数的平移,我们只需抓住点的平移.
把函数 y=2x+1 的图象向左平移3个单位,得到的
函数图象解析式为__________.
y=2x+7
O
x
y
y=2x+1
问题1
解:设平移后的函数解析式为y=k x+b (k≠0).
-3k+b = 1,
由题意得
b = 7.
解得
∴y=2x+7.
-2k +b= 3,
k = 2,
相当于y=2(x+3)+1.
1
1
把函数 y=2x+1 的图象向右平移3个单位,得到的
函数图象解析式为__________.
y=2x-5
O
x
y
y=2x+1
问题2
解:设平移后的函数解析式为y=k x+b (k≠0).
3k+b = 1,
由题意得
b = -5.
解得
∴y=2x-5.
4k +b= 3,
k = 2,
相当于y=2(x-3)+1.
1
1
一次函数图象左右平移规律
(1)若把直线y=k x+b (k≠0)沿x轴向左平移m个单位
长度,则平移后的函数解析式为 .
y=k(x+m) +b
(2)若把直线y=k x+b (k≠0)沿x轴向右平移m个单位
长度,则平移后的函数解析式为 .
y=k(x-m) +b
把函数 y=2x+1 的图象向上平移3个单位,得到的
函数图象解析式为__________.
y=2x+4
O
x
y
y=2x+1
问题3
解:设平移后的函数解析式为y=k x+b (k≠0).
b = 4,
由题意得
b = 4.
解得
∴y=2x+4.
k +b=6,
k = 2,
相当于y=2x+1+3.
1
1
把函数 y=2x+1 的图象向下平移3个单位,得到的
函数图象解析式为__________.
y=2x-2
O
x
y
y=2x+1
问题4
解:设平移后的函数解析式为y=k x+b (k≠0).
b = -2,
由题意得
b = -2.
解得
∴y=2x-2.
k +b=0,
k = 2,
相当于y=2x+1-3.
1
1
一次函数图象上下平移规律
(1)若把直线y=k x+b (k≠0)沿y轴向上平移n个单位
长度,则平移后的函数解析式为 .
y=k x+b +n
(2)若把直线y=k x+b (k≠0)沿y轴向下平移n个单位
长度,则平移后的函数解析式为 .
y=k x+b -n
换个角度去观察和思考,会
不会产生不同的效果,有别样的收获呢?
把函数 y=2x+1 的图象向左平移3个单位,得到的
函数图象解析式为__________.
y=2x+7
O
x
y
y=2x+1
问题1
也可以看作是向上
平移6个单位长度.
y=2x+1+6.
1
1
把函数 y=2x+1 的图象向右平移3个单位,得到的
函数图象解析式为__________.
y=2x-5
O
x
y
y=2x+1
问题2
下
6
也可以看作是向 平移 个单位长度.
y=2x+1-6.
1
1
把函数 y=2x+1 的图象向上平移3个单位,得到的
函数图象解析式为__________.
y=2x+4
O
x
y
y=2x+1
问题3
左
1.5
也可以看作是向 平移 个单位长度.
y=2(x+1.5)+1.
1
1
把函数 y=2x+1 的图象向下平移3个单位,得到的
函数图象解析式为__________.
y=2x-2
O
x
y
y=2x+1
问题4
右
1.5
也可以看作是向 平移 个单位长度.
y=2(x-1.5)+1.
1
1
平移口诀
左加右减自变量,上加下减常数项.
平移规律
(2)向上平移b + n,向下平移b-n.(改变b值)
(1)向左平移k(x + m),向右平移k(x - m) . (改变x值)
(3)平移前后的两个图象既可以上下平移得到,
也可以左右平移得到.
(4)平移不改变倾斜程度,所以不影响k值,
平移前后的两直线平行.
二、一次函数的平移规律在求函数表达式中的应用
例 写出将直线y=3x-2分别进行上、下、左、右平
移5个单位长度后的解析式.
解:
向上
y=3x-2+5
即y=3x+3
向下
y=3x-2-5
即y=3x-7
向左
y=3(x+5)-2
即y=3x+13
向右
y=3(x-5)-2
即y=3x-17
即时小练
1.在平面直角坐标系中,将直线l1: y=-3x-2 沿x轴
向左平移1个单位长度,再向上平移3个单位长度,
得到一条新的直线l2 ,则该直线l2的表达式为( )
A. y=-3x-9 B. y=-3x-2
C. y=-3x+2 D. y=-3x+9
y=-3(x+1)-2 +3
即y=-3x-2
B
A
2. 在平面直角坐标系中,将直线y=2x+1沿y轴向下平
移5个单位后,得到一条新的直线,该直线与x轴
的交点坐标是( )
A.(2,0) B.(-2,0)
C.(0,1) D.(0,-4)
3. 在平面直角坐标系中,将直线l1: y=-2x-2 平移
后,得到直线l2: y=-2x+4 ,则下列平移方法正
确的是( )
A.将l1向右平移4个单位长度
B.将l1向右平移6个单位长度
C.将l1向上平移2个单位长度
D.将l1向右平移3个单位长度
y=-2(x-4)-2
y=-2(x-6)-2
y=-2x-2+2
y=-2(x-3)-2
D
4. 在平面直角坐标系中,将直线y=kx-6 沿x轴向左
平移3个单位长度后恰好经过原点,则k的值为( )
A.-2 B.2
C.-3 D.3
y=k(x+3)-6
即y=kx+3k-6
把(0,0)代入y=kx+3k-6 中,
或3k-6 =0,
解得k=2.
B
5. 在平面直角坐标系中,将直线y=2x+m-1 沿x轴向左
平移3个单位长度后,得到一个正比例函数的图象,
则m的值为( )
A.-5 B.5
C.-6 D.6
y=2(x+3)+ m-1
即y=2x+ m+5
把(0,0)代入y=2x+m+5 中,
或m+5 =0,
解得m=-5.
A
6. 已知正比例函数y=kx(k ≠ 0)的图象过点(2,3),
把正比例函数y=kx (k ≠ 0)的图象平移,使它
过点(1,-1),则平移后的函数图象大致是( )
O
x
y
1
-1
O
x
y
1
-1
O
x
y
1
-1
-2
O
x
y
1
-1
-2
A. B. C. D.
D
K=1.5
y=1.5X+b
b=-2.5
与y轴交于(0,-2.5)
把(1,-1)代入得
y=1.5X-2.5
7. 如图,一次函数y=(m-3)x-m+1 的图象分别与x
轴、y轴的负半轴相交于A、B.
(2)若该一次函数向上平移1个单位长度就通过原
点,求m的值.
(1)求m的取值范围;
O
x
y
A
B
解:(1)
m-3 ﹤ 0,
由题意得
1﹤m﹤3.
解得
-m+1﹤ 0,
(2)平移后的解析式为 y=(m-3)x-m+2.
∵平移后过原点,
∴-m+2=0,
解得m=2.
素养提升
在平面直角坐标系中,一次函数y=kx+b (k≠0)的图 象由函数
y=0.5x的图象向下平移1个单位长度得到.
(1)求这个一次函数的解析式;
解:(1)
由题意知这个一次函数的解析式为y=0.5x-1.
(2)当x﹥-2时,对于x的每一个值,函数y=mx(m≠0)的值大于
一次函数y=kx+b (k≠0)的值,直接写出m的取值范围.
O
x
y
y=0.5x-1
m=1
(-2,-2)
m=0.5
m ﹤ 0.5
(2)0.5 ≤ m ≤ 1
m ﹥ 1
y=mx
( )
( )
( )
( )
( )
1
1
向右平移m个单位长度
Y=k(x – m)+b
向左平移m个单位长度
向下平移
n个
单位长度
向上平移
n个
单位长度
y=kx+b+ n
课堂小结
一次函数图象y=kx+b(k≠0)
y=kx+b- n
Y=k(x +m)+b
二次函数也是一样的原理.
用脑思考,
用心琢磨,
用行动证实.
