沪科版八年级数学下册19.3.2矩形的判定 课件(共19张PPT)
文档属性
| 名称 | 沪科版八年级数学下册19.3.2矩形的判定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 10:02:28 | ||
图片预览





文档简介
(共19张PPT)
如何由平行四边形得到一个矩形?
有一个角是直角的平行四边形叫做矩形
课题导入
定义法:
19.3.2 矩形的判定
课题导入
1.理解并掌握矩形的判定定理;
2.能应用矩形的判定解决简单的证明题和计算题.
目标引领
2分钟!
独立自学
1.思考矩形和一般平行四边形的区别.(边、角、对角线)
边:
矩形和一般平行四边形无区别,
都是“两组对边平行且相等”
角:
矩形的四个角都是直角
对角线:
矩形的对角线相等
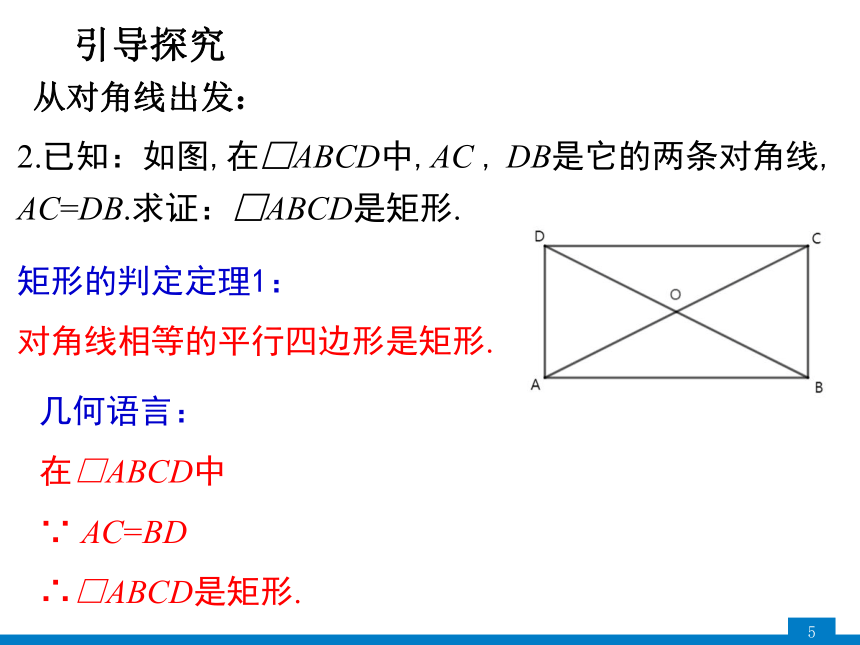
2.已知:如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.求证:□ABCD是矩形.
引导探究
从对角线出发:
矩形的判定定理1:
对角线相等的平行四边形是矩形.
几何语言:
在□ABCD中
∵ AC=BD
∴□ABCD是矩形.
思考1 数学来源于生活,事实上工人师傅在做门窗框架、桌面等包含矩形的物体时,不仅要测量矩形两组对边的长度是否分别相等,还要测量它们的两条对角线长度对角线是否相等,你现在知道为什么了吗?
引导探究
对角线相等的平行四边形是矩形.
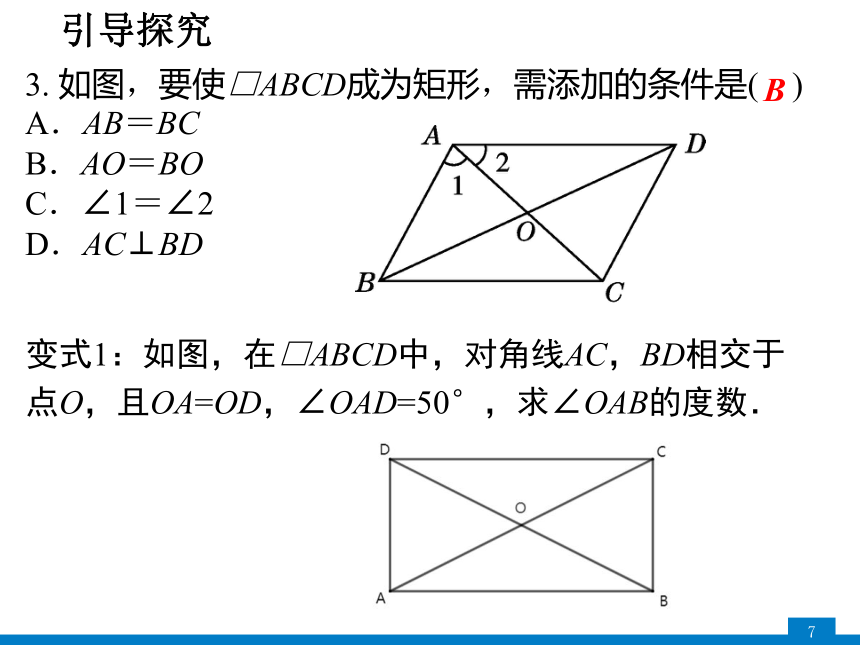
3. 如图,要使□ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AO=BO
C.∠1=∠2
D.AC⊥BD
B
引导探究
变式1:如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°,求∠OAB的度数.
引导探究
变式2:如图□ABCD中, ∠1= ∠2中.此时四边形ABCD是矩形吗?为什么?
引导探究
从角出发:
有一个角是直角的平行四边形叫做矩形
定义法:
4.如图,四边形ABCD的四个内角都是直角,求证:四边形ABCD是矩形.
思考2:是不是一定要知道四个角?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
引导探究
思考2:是不是一定要知道四个角?
5.已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
引导探究
矩形的判定定理2:
三个角是直角的四边形是矩形.
几何语言:
在四边形ABCD中
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形.
6. 如图,木工师傅要做一个矩形木框,做好以后测量得长AB=CD=80 cm,宽AD=BC=60 cm,对角线AC的长为1m,则这个木框 (填“合格”或“不合格”),判定的依据是 .
合格
有一个角是直角的平行四边形是矩形
引导探究
7.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、 ∠MCA、 ∠ ACN、∠CAF的平分线,则四边形ABCD是 ( )
A.梯形 B.平行四边形 C.矩形 D.不能确定
D
E
F
M
N
Q
P
A
B
C
C
引导探究
变式:
如图,□ABCD中,AE、BF、CG、DH分别是各内角的平分线,E、F、G、H为它们的交点,
求证:四边形EFGH的矩形.
结论:平行四边形四个内角的平分线围成的四边
形是矩形.
引导探究
8. 已知:如图,在△ABC中,AB=AC,点D是AC的中点,
直线AE∥BC,过点D作直线EF∥AB,分别交AE,BC于
点E,F.求证:四边形AECF是矩形.
A
B
C
D
E
F
引导探究
9.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
引导探究
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
目标升华
谈谈你这节课有哪些收获和疑惑?
1.如图,要使 ABCD成为矩形,需添加的条件是( )
A. AB=BC B. AC⊥BD
C.∠ABC=90° D. ∠ABC=∠CBD
2.如图,已知在四边形ABCD中,AC⊥BD且交于点O,E、F、G、H分别是四边的中点,
求证:四边形EFGH是矩形.
C
结论:顺次连接对角线互相垂直的四边形的中点
所围成的四边形是矩形.
当堂诊学
课本P89习题1,2
强化补清
如何由平行四边形得到一个矩形?
有一个角是直角的平行四边形叫做矩形
课题导入
定义法:
19.3.2 矩形的判定
课题导入
1.理解并掌握矩形的判定定理;
2.能应用矩形的判定解决简单的证明题和计算题.
目标引领
2分钟!
独立自学
1.思考矩形和一般平行四边形的区别.(边、角、对角线)
边:
矩形和一般平行四边形无区别,
都是“两组对边平行且相等”
角:
矩形的四个角都是直角
对角线:
矩形的对角线相等
2.已知:如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.求证:□ABCD是矩形.
引导探究
从对角线出发:
矩形的判定定理1:
对角线相等的平行四边形是矩形.
几何语言:
在□ABCD中
∵ AC=BD
∴□ABCD是矩形.
思考1 数学来源于生活,事实上工人师傅在做门窗框架、桌面等包含矩形的物体时,不仅要测量矩形两组对边的长度是否分别相等,还要测量它们的两条对角线长度对角线是否相等,你现在知道为什么了吗?
引导探究
对角线相等的平行四边形是矩形.
3. 如图,要使□ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AO=BO
C.∠1=∠2
D.AC⊥BD
B
引导探究
变式1:如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°,求∠OAB的度数.
引导探究
变式2:如图□ABCD中, ∠1= ∠2中.此时四边形ABCD是矩形吗?为什么?
引导探究
从角出发:
有一个角是直角的平行四边形叫做矩形
定义法:
4.如图,四边形ABCD的四个内角都是直角,求证:四边形ABCD是矩形.
思考2:是不是一定要知道四个角?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
引导探究
思考2:是不是一定要知道四个角?
5.已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
引导探究
矩形的判定定理2:
三个角是直角的四边形是矩形.
几何语言:
在四边形ABCD中
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形.
6. 如图,木工师傅要做一个矩形木框,做好以后测量得长AB=CD=80 cm,宽AD=BC=60 cm,对角线AC的长为1m,则这个木框 (填“合格”或“不合格”),判定的依据是 .
合格
有一个角是直角的平行四边形是矩形
引导探究
7.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、 ∠MCA、 ∠ ACN、∠CAF的平分线,则四边形ABCD是 ( )
A.梯形 B.平行四边形 C.矩形 D.不能确定
D
E
F
M
N
Q
P
A
B
C
C
引导探究
变式:
如图,□ABCD中,AE、BF、CG、DH分别是各内角的平分线,E、F、G、H为它们的交点,
求证:四边形EFGH的矩形.
结论:平行四边形四个内角的平分线围成的四边
形是矩形.
引导探究
8. 已知:如图,在△ABC中,AB=AC,点D是AC的中点,
直线AE∥BC,过点D作直线EF∥AB,分别交AE,BC于
点E,F.求证:四边形AECF是矩形.
A
B
C
D
E
F
引导探究
9.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
引导探究
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
目标升华
谈谈你这节课有哪些收获和疑惑?
1.如图,要使 ABCD成为矩形,需添加的条件是( )
A. AB=BC B. AC⊥BD
C.∠ABC=90° D. ∠ABC=∠CBD
2.如图,已知在四边形ABCD中,AC⊥BD且交于点O,E、F、G、H分别是四边的中点,
求证:四边形EFGH是矩形.
C
结论:顺次连接对角线互相垂直的四边形的中点
所围成的四边形是矩形.
当堂诊学
课本P89习题1,2
强化补清
