福建省清流一中2013届高三上学期第二阶段(半期)考试数学(理)试题
文档属性
| 名称 | 福建省清流一中2013届高三上学期第二阶段(半期)考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-22 00:00:00 | ||
图片预览


文档简介
清流一中2012-2013学年上学期半期考
高三数学试题(理科)
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合A={x|-2A.{x|02.下列函数与有相同图象的一个函数是( )
A. B. C. D.
3.函数的实数解落在的区间是( )
A. B. C. D.
4.平面向量,,若与共线,则的值为( )
A. B. C.1 D.4
5.若集合,则“”的充要条件是( )
A. B. C. D.
6.若,则=( )
A. B. C. D.-
7.若函数与在(0,+∞)上都是减函数,则在(0,+∞)上是( )
A.增函数 B.减函数 C.先增后减 D.先减后增
8. 某人向正东方向走后,向右转150°,然后朝新方向走3,结果他离出发点恰好是,那么的值为( )
A. B. C. 或 D.3
9.已知是腰长为2的等腰直角三角形,点是斜边上任意一点,则的值是( )
A.8 B.4 C.2 D.与点P的位置有关
10、设函数是定义在R上的函数,其中的导函数满足 对于恒成立,则 ( )
A. B.
C. D.
第II卷(非选择题 共100分)
二、填空题:本大题共5小题,每小题4分,共20分,
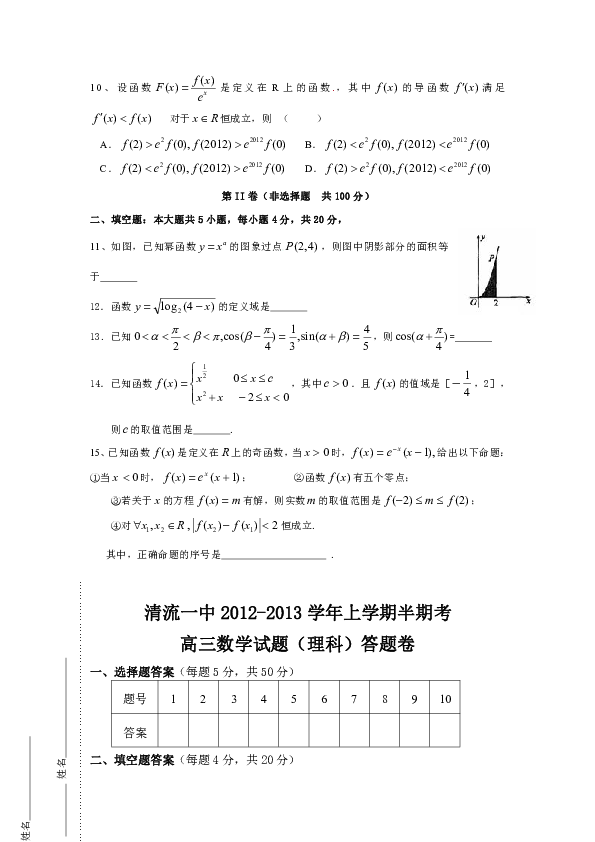
11、如图,已知幂函数的图象过点,则图中阴影部分的面积等于
12.函数的定义域是
13. 已知,则=
14.已知函数,其中.且的值域是[-,2],则的取值范围是 .
15、已知函数是定义在上的奇函数,当时,给出以下命题:①当时,; ②函数有五个零点;
③若关于的方程有解,则实数的取值范围是;
④对恒成立.
其中,正确命题的序号是 .
清流一中2012-2013学年上学期半期考
高三数学试题(理科)答题卷
一、选择题答案(每题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题答案(每题4分,共20分)
11、________________ _, 12、______________
13、 , 14、 , 15、 .
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
16. (本小题满分13分)已知平面上三个向量、、的模均为1,它们相互之间的夹角均为120°.(1)求证:-;
(2)若>1 ,求的取值范围.
17.(本小题满分13分)已知命题实数满足,命题实数满足,若是的必要不充分条件,求实数的取值范围.
18. (本小题满分13分)函数
(,,)的一段图象如图所示.
(1)求函数的解析式;
(2)将函数的图象向右平移个单位,得到的图象,求函数的图象的对称轴和对称中心.
19.(本小题满分13分)△ABC的三个内角A,B,C所对的边分别为,,,向量,,且.
(1)求A的大小;(2)现给出下列三个条件:①;②;③.试从中再选择两个条件以确定△ABC,求出你所确定的△ABC的面积。
20.(本小题满分14分)某工厂生产某种产品,每日的成本C (单位:元)与日产里 (单位:吨)满足函数关系式,每日的销售额(单位:元)与日产量满足函数关系式
已知每日的利润,且当时.
(1)求的值;(2)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值.
21.(本小题满分14分)
已知函数在点的切线方程为.
(1)求函数的解析式;
(2)设,求证:在上恒成立;
(3)已知,求证:
清流一中2012-2013学年上学期半期考高三数学试题(理科)参考答案及评分标准
一、选择题:1-5:ADBBC 6-10:DBCBB
二、填空题: 11. 12. 13. 14. (0,4] 15. ①④
三.解答题:
16.(1)证明 ∵-,
∴-. …………………5分
(2)解>1>1.
∵||=||=1,且、的夹角均为120°,
∴==1,·=-,
∴+1->1,即->0,∴>1或<0. …………………13分
17、解 :由,得, …………………3分
∴记
由得,…………………6分
记
∵是的必要不充分条件
∴是的充分不必要条件, 即且, ∴,…………………8分
要使,又,则只需 …………………11分
∴
故所求实数的取值范围是. …………………13分
18. 解:(1)由题图知A=2,,于是,
将的图象向左平移个单位长度,得 的图象.
于是,∴. …………………6分
(2)依题意得. ……………8分
故.…10分
由,得.
由,得.
∴的对称轴为, 对称中心为
19.解:(1), …………2分
∴ …………4分
, …………………………5分
,所以 ……………………………………6分
(2)方案一:选择①③可确定△ABC。 …………………………………………7分
由余弦定理 ………… 9分
整理得 …………………………12分
…………13分
方案二:选择①②可确定△ABC。 ……………………………………………7分
又…9分
由正弦定理得 …………12分
…………13分
(注:选择②③不能确定三角形)20.解:由题意可得:……………………2分
20.
21、解:(1)将代入切线方程得
∴,化简得 ………………………2分
又
∴ 解得:.
∴ . …………………………4分
(2)由已知得在上恒成立,化简得
即在上恒成立 …………………………5分
设,则, ………6分
∴,,即
∴在上单调递增, …………………………8分
∴=0
∴在上恒成立. …………………………10分
(3) ∴
由(2)知,有 整理得
∴当时,. …………………………14分
高三数学试题(理科)
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合A={x|-2
A. B. C. D.
3.函数的实数解落在的区间是( )
A. B. C. D.
4.平面向量,,若与共线,则的值为( )
A. B. C.1 D.4
5.若集合,则“”的充要条件是( )
A. B. C. D.
6.若,则=( )
A. B. C. D.-
7.若函数与在(0,+∞)上都是减函数,则在(0,+∞)上是( )
A.增函数 B.减函数 C.先增后减 D.先减后增
8. 某人向正东方向走后,向右转150°,然后朝新方向走3,结果他离出发点恰好是,那么的值为( )
A. B. C. 或 D.3
9.已知是腰长为2的等腰直角三角形,点是斜边上任意一点,则的值是( )
A.8 B.4 C.2 D.与点P的位置有关
10、设函数是定义在R上的函数,其中的导函数满足 对于恒成立,则 ( )
A. B.
C. D.
第II卷(非选择题 共100分)
二、填空题:本大题共5小题,每小题4分,共20分,
11、如图,已知幂函数的图象过点,则图中阴影部分的面积等于
12.函数的定义域是
13. 已知,则=
14.已知函数,其中.且的值域是[-,2],则的取值范围是 .
15、已知函数是定义在上的奇函数,当时,给出以下命题:①当时,; ②函数有五个零点;
③若关于的方程有解,则实数的取值范围是;
④对恒成立.
其中,正确命题的序号是 .
清流一中2012-2013学年上学期半期考
高三数学试题(理科)答题卷
一、选择题答案(每题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题答案(每题4分,共20分)
11、________________ _, 12、______________
13、 , 14、 , 15、 .
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
16. (本小题满分13分)已知平面上三个向量、、的模均为1,它们相互之间的夹角均为120°.(1)求证:-;
(2)若>1 ,求的取值范围.
17.(本小题满分13分)已知命题实数满足,命题实数满足,若是的必要不充分条件,求实数的取值范围.
18. (本小题满分13分)函数
(,,)的一段图象如图所示.
(1)求函数的解析式;
(2)将函数的图象向右平移个单位,得到的图象,求函数的图象的对称轴和对称中心.
19.(本小题满分13分)△ABC的三个内角A,B,C所对的边分别为,,,向量,,且.
(1)求A的大小;(2)现给出下列三个条件:①;②;③.试从中再选择两个条件以确定△ABC,求出你所确定的△ABC的面积。
20.(本小题满分14分)某工厂生产某种产品,每日的成本C (单位:元)与日产里 (单位:吨)满足函数关系式,每日的销售额(单位:元)与日产量满足函数关系式
已知每日的利润,且当时.
(1)求的值;(2)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值.
21.(本小题满分14分)
已知函数在点的切线方程为.
(1)求函数的解析式;
(2)设,求证:在上恒成立;
(3)已知,求证:
清流一中2012-2013学年上学期半期考高三数学试题(理科)参考答案及评分标准
一、选择题:1-5:ADBBC 6-10:DBCBB
二、填空题: 11. 12. 13. 14. (0,4] 15. ①④
三.解答题:
16.(1)证明 ∵-,
∴-. …………………5分
(2)解>1>1.
∵||=||=1,且、的夹角均为120°,
∴==1,·=-,
∴+1->1,即->0,∴>1或<0. …………………13分
17、解 :由,得, …………………3分
∴记
由得,…………………6分
记
∵是的必要不充分条件
∴是的充分不必要条件, 即且, ∴,…………………8分
要使,又,则只需 …………………11分
∴
故所求实数的取值范围是. …………………13分
18. 解:(1)由题图知A=2,,于是,
将的图象向左平移个单位长度,得 的图象.
于是,∴. …………………6分
(2)依题意得. ……………8分
故.…10分
由,得.
由,得.
∴的对称轴为, 对称中心为
19.解:(1), …………2分
∴ …………4分
, …………………………5分
,所以 ……………………………………6分
(2)方案一:选择①③可确定△ABC。 …………………………………………7分
由余弦定理 ………… 9分
整理得 …………………………12分
…………13分
方案二:选择①②可确定△ABC。 ……………………………………………7分
又…9分
由正弦定理得 …………12分
…………13分
(注:选择②③不能确定三角形)20.解:由题意可得:……………………2分
20.
21、解:(1)将代入切线方程得
∴,化简得 ………………………2分
又
∴ 解得:.
∴ . …………………………4分
(2)由已知得在上恒成立,化简得
即在上恒成立 …………………………5分
设,则, ………6分
∴,,即
∴在上单调递增, …………………………8分
∴=0
∴在上恒成立. …………………………10分
(3) ∴
由(2)知,有 整理得
∴当时,. …………………………14分
同课章节目录
