九下专题复习10—圆的复习典型例题
图片预览

文档简介
课题
圆的复习课——典型例题
教学目标:
经历提取定理条件,构造基本图形的过程,体会添加辅助线的方法.
明确圆中的问题可以转化为直线型知识来解决.
初步形成解决综合题的思路与方法.
在探究过程中,积累解题经验,增加解题信心.
重点:明确圆中的问题可以转化为直线型知识来解决.
难点:能够通过提取定理条件,构造基本图形的方法来添加辅助线.
教具准备:多媒体,三角板,学案.
教学环节
教师活动
学生活动
设计意图
活动一、小题悟方法
活动二:
典例学经验
活动三:
小结
1、已知:如图,AB过圆心O,∠C=30°.
①求∠ABD的度数.
分析:
方法一:见直径封闭圆周角,构造直角三角形.
方法二:见圆周角想圆心角,构造等边三角形.
教师提问:你如何想到连接AD?连接OD?
建立模型:
1、已知:如图,AB过圆心O,∠C=30°.
②当点P是OB中点,⊙O的半径为1时,求CD的长.
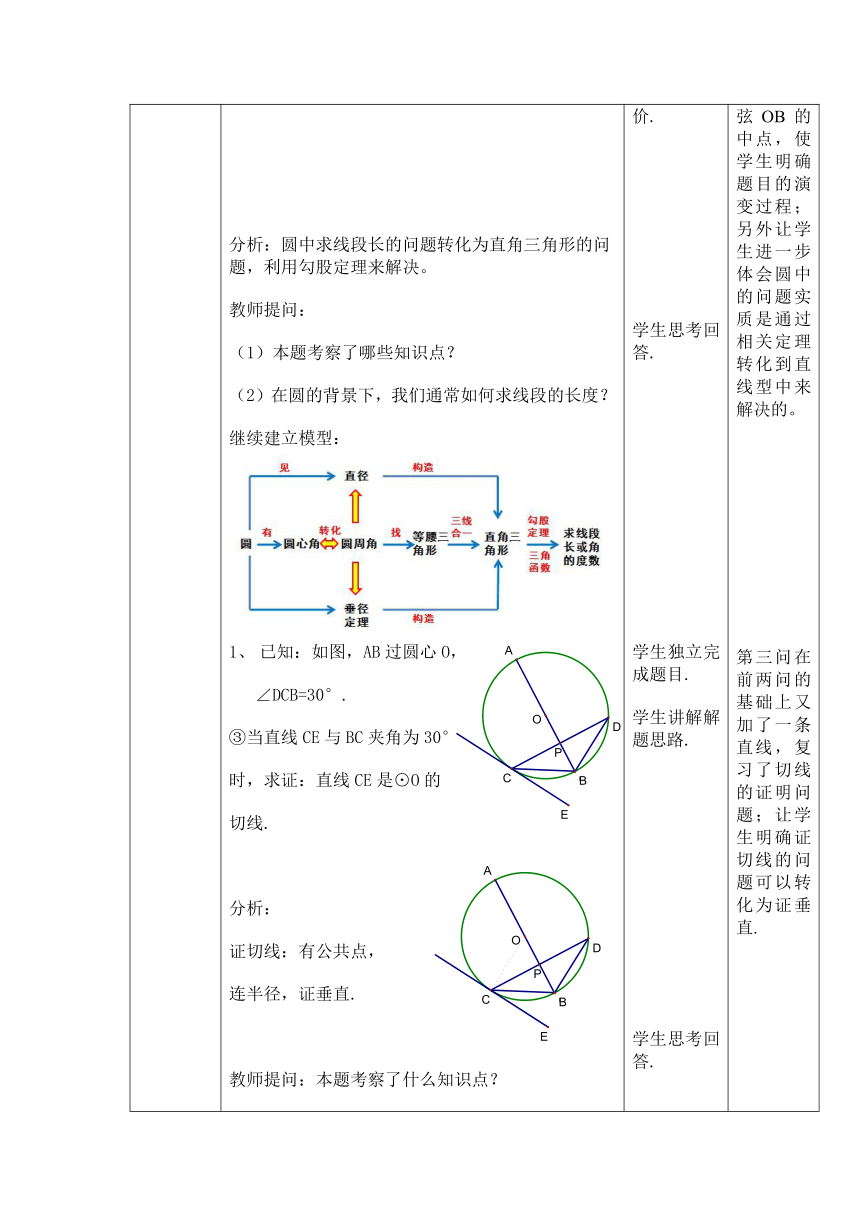
分析:圆中求线段长的问题转化为直角三角形的问题,利用勾股定理来解决。
教师提问:
(1)本题考察了哪些知识点?
(2)在圆的背景下,我们通常如何求线段的长度?
继续建立模型:
已知:如图,AB过圆心O,
∠DCB=30°.
③当直线CE与BC夹角为30°
时,求证:直线CE是⊙O的
切线.
分析:
证切线:有公共点,
连半径,证垂直.
教师提问:本题考察了什么知识点?
继续完成建模:
总结:
(1)回顾这道题,你有什么体会?
(2)如果有一个陌生的图形摆在你面前,你会怎么想?
(3)在学案纸上构造定理基本图.
教师出示第3题:
3、已知:如图,△ABC内接于⊙O,BD垂直半径AO于D.
(1)求证:∠C=∠ABD;
(2)若BD=4,∠C=60°,求⊙O的半径.
分析:
方法一:补全直径,封闭圆周角.
方法二:构造垂径定理基本图
师:现在,大家回顾一下本节课的学习过程,想一想, 本节课都有哪些收获?
你认为本节课的重点是什么?
你还有哪些疑点?
引导学生分组交流课堂心得,或整理笔记
学生独立完成题目。
学生讲解自己的做法,其他学生进行评价。
学生思考回答,发表自己的见解.
学生独立思考解答.
学生讲解解题思路,其他同学评价.
学生思考回答.
学生独立完成题目.
学生讲解解题思路.
学生思考回答.
学生思考回答.
学生思考,在学案上补图.
学生独立完成题目.
一名同学到黑板上板书(或实物投影).
学生归纳总结本节课所学内容.
以简单小题复习圆周角定理及其推论,让学生悟出方法,通过构造定理基本图添加辅助线。并揭示圆与直角三角形、等腰三角形的联系。
第二问在第一问的基础上让直径AB的位置更特殊,过弦OB的中点,使学生明确题目的演变过程;另外让学生进一步体会圆中的问题实质是通过相关定理转化到直线型中来解决的。
第三问在前两问的基础上又加了一条直线,复习了切线的证明问题;让学生明确证切线的问题可以转化为证垂直.
学生及时归纳总结,培养良好的学习习惯.
这道题第一问证角等需要学生通过补全定理基本图来添加辅助线。
第二问需要构造直角三角形求线段长。
理清知识脉络和使用方法;强化所学知识和技能技巧.
附:板书设计
圆复习——典型例题
圆的复习课——典型例题
教学目标:
经历提取定理条件,构造基本图形的过程,体会添加辅助线的方法.
明确圆中的问题可以转化为直线型知识来解决.
初步形成解决综合题的思路与方法.
在探究过程中,积累解题经验,增加解题信心.
重点:明确圆中的问题可以转化为直线型知识来解决.
难点:能够通过提取定理条件,构造基本图形的方法来添加辅助线.
教具准备:多媒体,三角板,学案.
教学环节
教师活动
学生活动
设计意图
活动一、小题悟方法
活动二:
典例学经验
活动三:
小结
1、已知:如图,AB过圆心O,∠C=30°.
①求∠ABD的度数.
分析:
方法一:见直径封闭圆周角,构造直角三角形.
方法二:见圆周角想圆心角,构造等边三角形.
教师提问:你如何想到连接AD?连接OD?
建立模型:
1、已知:如图,AB过圆心O,∠C=30°.
②当点P是OB中点,⊙O的半径为1时,求CD的长.
分析:圆中求线段长的问题转化为直角三角形的问题,利用勾股定理来解决。
教师提问:
(1)本题考察了哪些知识点?
(2)在圆的背景下,我们通常如何求线段的长度?
继续建立模型:
已知:如图,AB过圆心O,
∠DCB=30°.
③当直线CE与BC夹角为30°
时,求证:直线CE是⊙O的
切线.
分析:
证切线:有公共点,
连半径,证垂直.
教师提问:本题考察了什么知识点?
继续完成建模:
总结:
(1)回顾这道题,你有什么体会?
(2)如果有一个陌生的图形摆在你面前,你会怎么想?
(3)在学案纸上构造定理基本图.
教师出示第3题:
3、已知:如图,△ABC内接于⊙O,BD垂直半径AO于D.
(1)求证:∠C=∠ABD;
(2)若BD=4,∠C=60°,求⊙O的半径.
分析:
方法一:补全直径,封闭圆周角.
方法二:构造垂径定理基本图
师:现在,大家回顾一下本节课的学习过程,想一想, 本节课都有哪些收获?
你认为本节课的重点是什么?
你还有哪些疑点?
引导学生分组交流课堂心得,或整理笔记
学生独立完成题目。
学生讲解自己的做法,其他学生进行评价。
学生思考回答,发表自己的见解.
学生独立思考解答.
学生讲解解题思路,其他同学评价.
学生思考回答.
学生独立完成题目.
学生讲解解题思路.
学生思考回答.
学生思考回答.
学生思考,在学案上补图.
学生独立完成题目.
一名同学到黑板上板书(或实物投影).
学生归纳总结本节课所学内容.
以简单小题复习圆周角定理及其推论,让学生悟出方法,通过构造定理基本图添加辅助线。并揭示圆与直角三角形、等腰三角形的联系。
第二问在第一问的基础上让直径AB的位置更特殊,过弦OB的中点,使学生明确题目的演变过程;另外让学生进一步体会圆中的问题实质是通过相关定理转化到直线型中来解决的。
第三问在前两问的基础上又加了一条直线,复习了切线的证明问题;让学生明确证切线的问题可以转化为证垂直.
学生及时归纳总结,培养良好的学习习惯.
这道题第一问证角等需要学生通过补全定理基本图来添加辅助线。
第二问需要构造直角三角形求线段长。
理清知识脉络和使用方法;强化所学知识和技能技巧.
附:板书设计
圆复习——典型例题
同课章节目录
