九下专题复习13—旋转与等腰

课题
旋转与等腰三角形
授课年级
九
课型
复习课
三维
教学目标
1.通过题目训练，深化对旋转变换的理解，体会旋转与等腰三角形之间的关系；
2.经历题目的思考与反思的过程，体会研究图形旋转的思想方法，逐步形成用旋转的视角识别图形与构造图形的基本解题策略；
3. 培养学生把已有知识建立联系的良好习惯。
教学重点
逐步形成用旋转的视角识别图形与构造图形的基本解题意识。
教学难点
掌握用旋转的眼光识别图形与构造图形的基本策略。
教学辅助手段
多媒体
教学方法
讲授法、启发法、探究式
教
学
流
程
教师活动
学生活动
设计意图
活
动
1
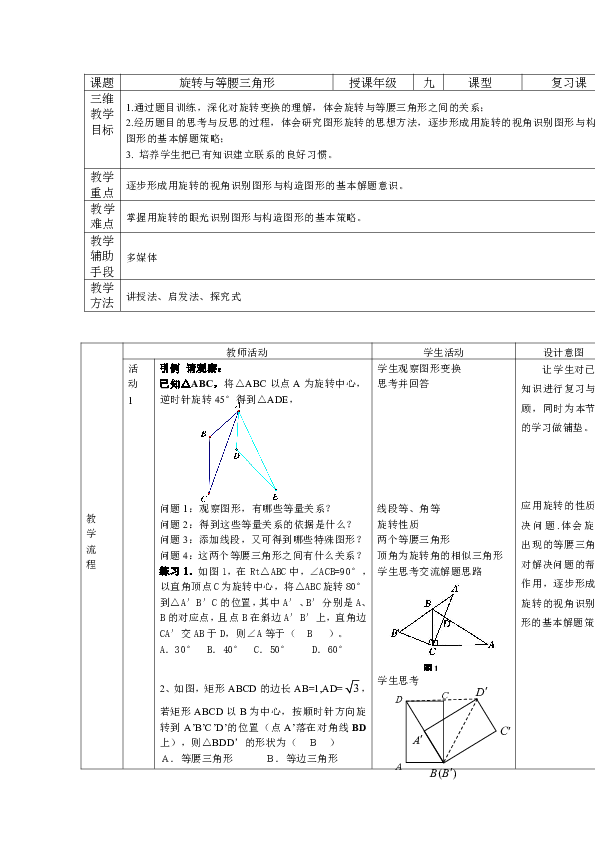
引例 请观察：
已知△ABC，将△ABC以点A为旋转中心，逆时针旋转45°得到△ADE，
问题1：观察图形，有哪些等量关系？
问题2：得到这些等量关系的依据是什么？
问题3：添加线段，又可得到哪些特殊图形？
问题4：这两个等腰三角形之间有什么关系？
练习1．如图1，在Rt△ABC中，∠ACB=90°，以直角顶点C为旋转中心，将△ABC旋转80°到△A′B′C的位置，其中A′、B′分别是A、B的对应点，且点B在斜边A′B′上，直角边CA′交AB于D，则∠A等于（ B ）。
A．30° B．40° C．50° D．60°
2、如图，矩形ABCD的边长AB=1,AD=，若矩形ABCD以B为中心，按顺时针方向旋转到A’B’C’D’的位置（点A’落在对角线BD上），则△BDD’的形状为（　Ｂ　）
Ａ．等腰三角形 Ｂ．等边三角形
Ｃ．等腰直角三角形 Ｄ．无法确定
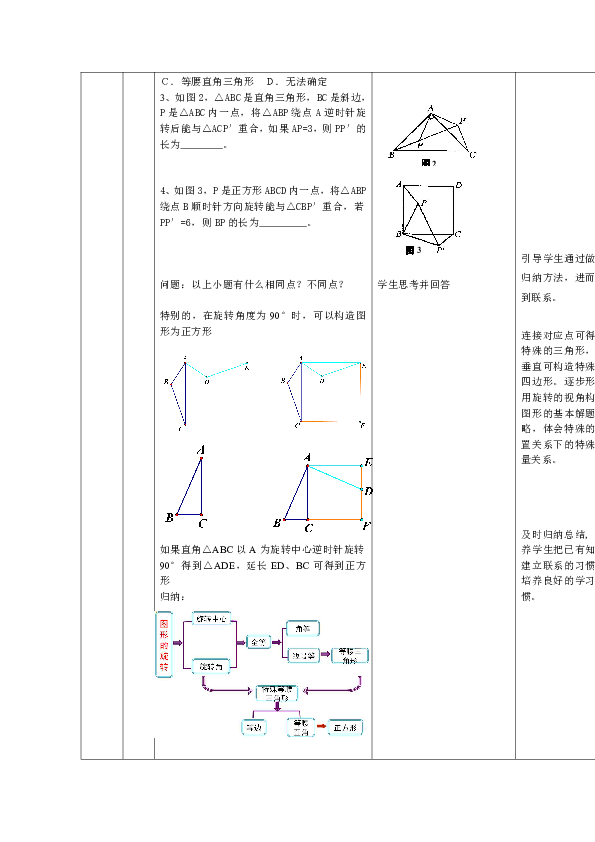
3、如图2，△ABC是直角三角形，BC是斜边，P是△ABC内一点，将△ABP绕点A逆时针旋转后能与△ACP′重合，如果AP=3，则PP′的长为 。
4、如图3，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若PP′=6，则BP的长为 。
问题：以上小题有什么相同点？不同点？
特别的，在旋转角度为90°时，可以构造图形为正方形
如果直角△ABC以A为旋转中心逆时针旋转90°得到△ADE，延长ED、BC可得到正方形
归纳：
学生观察图形变换
思考并回答
线段等、角等
旋转性质
两个等腰三角形
顶角为旋转角的相似三角形
学生思考交流解题思路
学生思考
学生思考并回答
让学生对已有知识进行复习与回顾，同时为本节课的学习做铺垫。

应用旋转的性质解决问题.体会旋转出现的等腰三角形对解决问题的帮助作用，逐步形成用旋转的视角识别图形的基本解题策略
引导学生通过做题归纳方法，进而找到联系。
连接对应点可得到特殊的三角形，做垂直可构造特殊的四边形。逐步形成用旋转的视角构造图形的基本解题策略，体会特殊的位置关系下的特殊数量关系。
及时归纳总结, 培养学生把已有知识建立联系的习惯，培养良好的学习习惯。
活动
2
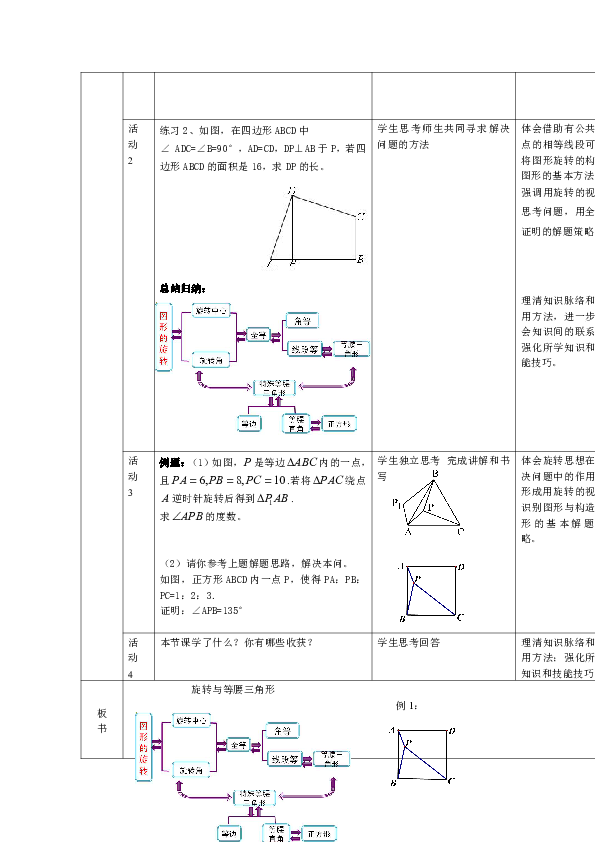
练习2、如图，在四边形ABCD中
∠ ADC=∠B=90°，AD=CD，DP⊥AB于P，若四边形ABCD的面积是16，求DP的长。
总结归纳：
学生思考师生共同寻求解决问题的方法
体会借助有公共端点的相等线段可以将图形旋转的构造图形的基本方法。
强调用旋转的视角思考问题，用全等证明的解题策略。
理清知识脉络和使用方法，进一步体会知识间的联系，强化所学知识和技能技巧。
活动
3
例题：（1）如图，是等边内的一点，且.若将绕点逆时针旋转后得到.
求的度数。
（2）请你参考上题解题思路，解决本问。
如图，正方形ABCD内一点P，使得PA：PB：PC=1：2：3. 
证明：∠APB=135°
学生独立思考 完成讲解和书写
体会旋转思想在解决问题中的作用，形成用旋转的视角识别图形与构造图形的基本解题策略。
活
动
4
本节课学了什么？你有哪些收获？
学生思考回答
理清知识脉络和使用方法；强化所学知识和技能技巧。
板
书
旋转与等腰三角形
例1：
作业
目标检测39，42
课后
反思