九下专题复习7—相似三角形的基本图形1
文档属性
| 名称 | 九下专题复习7—相似三角形的基本图形1 |  | |
| 格式 | zip | ||
| 文件大小 | 102.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-22 15:35:56 | ||
图片预览

文档简介
课 题
相似的基本图形(一)
一、教学目标:
1、进一步认识相似三角形中的基本图形“A”字形、“8”字形,并会运用其进行推理与计算;
2、在解题的过程中体会基本图形的重要性,养成在学习过程中及时总结的习惯;
3、数学思想方法的渗透及一题多解的问题解决激发学生学习数学的兴趣,体验收获的快乐.
二、重点、难点:
重点:应用基本图形解决问题.
难点:构造基本图形解决问题
三、教学过程设计:
问题与情境
师生行为
设计意图
【活动一】
小题得基本图形
问题1:
(1)如图1,当 时,△ABC∽△ADE;
(2)如图2,当 时,△ABC∽△AED;
(3)如图3,当 时,△ABC∽△ACD.
图1 图2
图3 图4
(4)如图4,在Rt△ABC中, ∠ACB=90°, DE⊥AB,则△ ∽△___
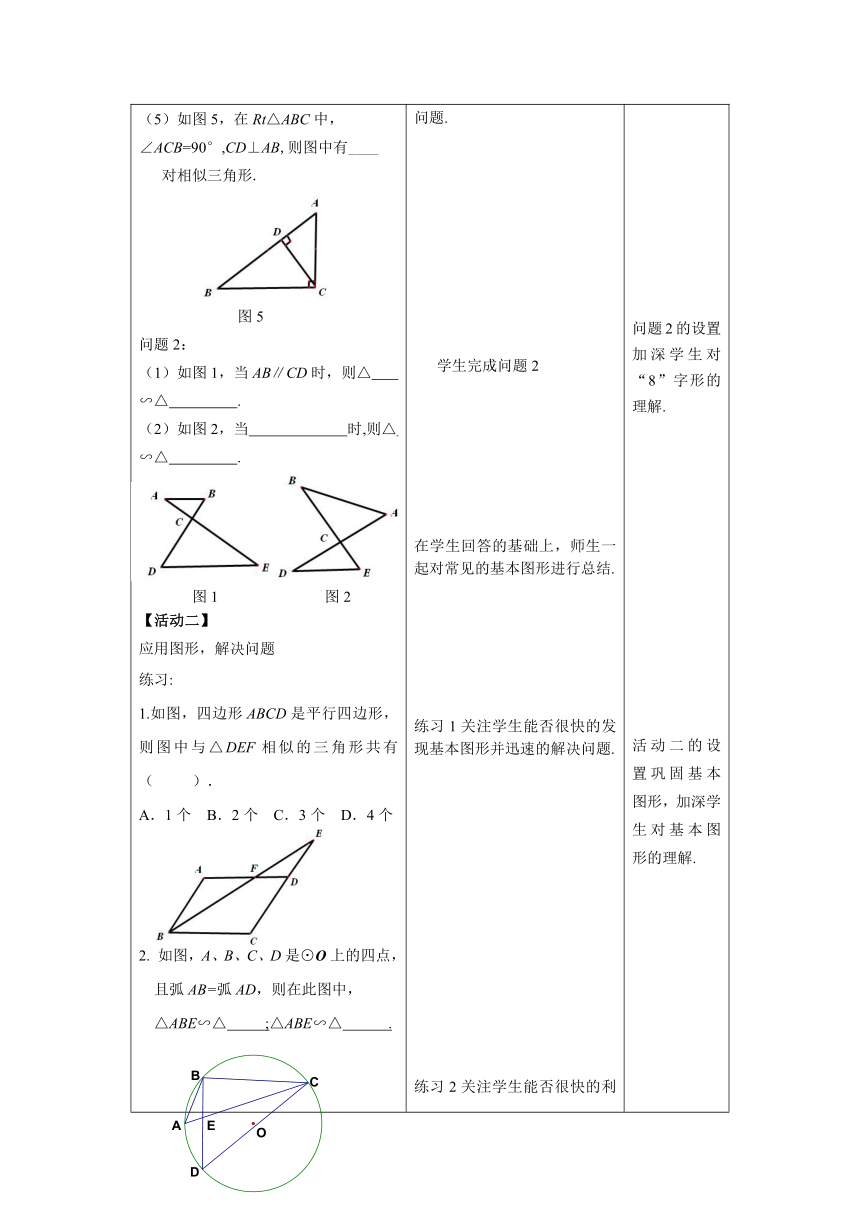
(5)如图5,在Rt△ABC中,
∠ACB=90°,CD⊥AB,则图中有____ 对相似三角形.
图5
问题2:
(1)如图1,当AB∥CD时,则△ ∽△ .
(2)如图2,当 时,则△ ∽△ .
图1 图2
【活动二】
应用图形,解决问题
练习:
1.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( ).
A.1个 B.2个 C.3个 D.4个
2. 如图,A、B、C、D是⊙O上的四点,
且弧AB=弧AD,则在此图中,
△ABE∽△ ;△ABE∽△ .
3.如图,在△ABC中,D、E分别是AB,AC上一点,且∠AED =∠B. 若AE=5,AB= 9,CB=6,则ED的长是_________
【活动三】
典型例题,深化提高
例1.如图,CD是Rt△ABC斜边上的高,∠ACB=90°,E为AC的中点,ED交CB的延长线于F.
求证:△CDF∽△DBF.
例2.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O、B、P为顶点的三角形与△ABC相似,则点P的坐标是_____________
例3:如图,△ABC中,D是BC的中点,E 是AB上一点,AD、CE相交于F.若,
求证:.
【活动四】
课堂小结,巩固知识
对今天的基本图形的研究,你有什么收获?
教师出示问题1,学生回答问题.
教师关注学生能否很快地解决问题,并做到有理有据.
教师关注学生能否很快的解决问题.
学生完成问题2
在学生回答的基础上,师生一起对常见的基本图形进行总结.
练习1关注学生能否很快的发现基本图形并迅速的解决问题.
练习2关注学生能否很快的利用圆的知识结合相似的基本图形解决问题.
练习3 关注学生能否很快的发现基本图形并进行问题的转化,从而准确的解决问题.
例1的解答在教师给出问题串的基础上来完成.问题如下:
①你发现图中的基本图形吗?如果有是哪个基本图形?
②由这个基本图形可以得到什么条件?
③我们要证明相似的这对三角形有什么特点?还需要什么条件可以证明相似?
学生在教师的引导下解决问题
例2关注学生能否准确的理解题意再利用相似解决问题.
例题3学生在教师的引导下完成,教师注意观察学生能否较快的构造基本图形解决问题,同时注意观察学生的不同解法.
不同解法的学生展示自己的解题思路.
学生在教师的引导下进行课堂知识归纳.
通过一组小题的解答,加深对“A”字形的理解.
问题2的设置加深学生对“8”字形的理解.
活动二的设置巩固基本图形,加深学生对基本图形的理解.
例1的解决进一步让学生体会到基本图形的重要性.
例2在体会基本图形重要性的同时注意分类讨论的数学思想.
例题3的解答,学生体会结合题中条件,构造基本图形解决问题.
课堂小结帮助学生理清本节课的知识重点,培养学生归纳、总结的能力.
课 题
相似的基本图形(一)
一、教学目标:
1、进一步认识相似三角形中的基本图形“A”字形、“8”字形,并会运用其进行推理与计算;
2、在解题的过程中体会基本图形的重要性,养成在学习过程中及时总结的习惯;
3、数学思想方法的渗透及一题多解的问题解决激发学生学习数学的兴趣,体验收获的快乐.
二、重点、难点:
重点:应用基本图形解决问题.
难点:构造基本图形解决问题
三、教学过程设计:
问题与情境
师生行为
设计意图
【活动一】
小题得基本图形
问题1:
(1)如图1,当 时,△ABC∽△ADE;
(2)如图2,当 时,△ABC∽△AED;
(3)如图3,当 时,△ABC∽△ACD.
图1 图2
图3 图4
(4)如图4,在Rt△ABC中, ∠ACB=90°, DE⊥AB,则△ ∽△___
(5)如图5,在Rt△ABC中,
∠ACB=90°,CD⊥AB,则图中有____ 对相似三角形.
图5
问题2:
(1)如图1,当AB∥CD时,则△ ∽△ .
(2)如图2,当 时,则△ ∽△ .
图1 图2
【活动二】
应用图形,解决问题
练习:
1.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( ).
A.1个 B.2个 C.3个 D.4个
2. 如图,A、B、C、D是⊙O上的四点,
且弧AB=弧AD,则在此图中,
△ABE∽△ ;△ABE∽△ .
3.如图,在△ABC中,D、E分别是AB,AC上一点,且∠AED =∠B. 若AE=5,AB= 9,CB=6,则ED的长是_________
【活动三】
典型例题,深化提高
例1.如图,CD是Rt△ABC斜边上的高,∠ACB=90°,E为AC的中点,ED交CB的延长线于F.
求证:△CDF∽△DBF.
例2.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O、B、P为顶点的三角形与△ABC相似,则点P的坐标是_____________
例3:如图,△ABC中,D是BC的中点,E 是AB上一点,AD、CE相交于F.若,
求证:.
【活动四】
课堂小结,巩固知识
对今天的基本图形的研究,你有什么收获?
教师出示问题1,学生回答问题.
教师关注学生能否很快地解决问题,并做到有理有据.
教师关注学生能否很快的解决问题.
学生完成问题2
在学生回答的基础上,师生一起对常见的基本图形进行总结.
练习1关注学生能否很快的发现基本图形并迅速的解决问题.
练习2关注学生能否很快的利用圆的知识结合相似的基本图形解决问题.
练习3 关注学生能否很快的发现基本图形并进行问题的转化,从而准确的解决问题.
例1的解答在教师给出问题串的基础上来完成.问题如下:
①你发现图中的基本图形吗?如果有是哪个基本图形?
②由这个基本图形可以得到什么条件?
③我们要证明相似的这对三角形有什么特点?还需要什么条件可以证明相似?
学生在教师的引导下解决问题
例2关注学生能否准确的理解题意再利用相似解决问题.
例题3学生在教师的引导下完成,教师注意观察学生能否较快的构造基本图形解决问题,同时注意观察学生的不同解法.
不同解法的学生展示自己的解题思路.
学生在教师的引导下进行课堂知识归纳.
通过一组小题的解答,加深对“A”字形的理解.
问题2的设置加深学生对“8”字形的理解.
活动二的设置巩固基本图形,加深学生对基本图形的理解.
例1的解决进一步让学生体会到基本图形的重要性.
例2在体会基本图形重要性的同时注意分类讨论的数学思想.
例题3的解答,学生体会结合题中条件,构造基本图形解决问题.
课堂小结帮助学生理清本节课的知识重点,培养学生归纳、总结的能力.
相似的基本图形(一)
一、教学目标:
1、进一步认识相似三角形中的基本图形“A”字形、“8”字形,并会运用其进行推理与计算;
2、在解题的过程中体会基本图形的重要性,养成在学习过程中及时总结的习惯;
3、数学思想方法的渗透及一题多解的问题解决激发学生学习数学的兴趣,体验收获的快乐.
二、重点、难点:
重点:应用基本图形解决问题.
难点:构造基本图形解决问题
三、教学过程设计:
问题与情境
师生行为
设计意图
【活动一】
小题得基本图形
问题1:
(1)如图1,当 时,△ABC∽△ADE;
(2)如图2,当 时,△ABC∽△AED;
(3)如图3,当 时,△ABC∽△ACD.
图1 图2
图3 图4
(4)如图4,在Rt△ABC中, ∠ACB=90°, DE⊥AB,则△ ∽△___
(5)如图5,在Rt△ABC中,
∠ACB=90°,CD⊥AB,则图中有____ 对相似三角形.
图5
问题2:
(1)如图1,当AB∥CD时,则△ ∽△ .
(2)如图2,当 时,则△ ∽△ .
图1 图2
【活动二】
应用图形,解决问题
练习:
1.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( ).
A.1个 B.2个 C.3个 D.4个
2. 如图,A、B、C、D是⊙O上的四点,
且弧AB=弧AD,则在此图中,
△ABE∽△ ;△ABE∽△ .
3.如图,在△ABC中,D、E分别是AB,AC上一点,且∠AED =∠B. 若AE=5,AB= 9,CB=6,则ED的长是_________
【活动三】
典型例题,深化提高
例1.如图,CD是Rt△ABC斜边上的高,∠ACB=90°,E为AC的中点,ED交CB的延长线于F.
求证:△CDF∽△DBF.
例2.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O、B、P为顶点的三角形与△ABC相似,则点P的坐标是_____________
例3:如图,△ABC中,D是BC的中点,E 是AB上一点,AD、CE相交于F.若,
求证:.
【活动四】
课堂小结,巩固知识
对今天的基本图形的研究,你有什么收获?
教师出示问题1,学生回答问题.
教师关注学生能否很快地解决问题,并做到有理有据.
教师关注学生能否很快的解决问题.
学生完成问题2
在学生回答的基础上,师生一起对常见的基本图形进行总结.
练习1关注学生能否很快的发现基本图形并迅速的解决问题.
练习2关注学生能否很快的利用圆的知识结合相似的基本图形解决问题.
练习3 关注学生能否很快的发现基本图形并进行问题的转化,从而准确的解决问题.
例1的解答在教师给出问题串的基础上来完成.问题如下:
①你发现图中的基本图形吗?如果有是哪个基本图形?
②由这个基本图形可以得到什么条件?
③我们要证明相似的这对三角形有什么特点?还需要什么条件可以证明相似?
学生在教师的引导下解决问题
例2关注学生能否准确的理解题意再利用相似解决问题.
例题3学生在教师的引导下完成,教师注意观察学生能否较快的构造基本图形解决问题,同时注意观察学生的不同解法.
不同解法的学生展示自己的解题思路.
学生在教师的引导下进行课堂知识归纳.
通过一组小题的解答,加深对“A”字形的理解.
问题2的设置加深学生对“8”字形的理解.
活动二的设置巩固基本图形,加深学生对基本图形的理解.
例1的解决进一步让学生体会到基本图形的重要性.
例2在体会基本图形重要性的同时注意分类讨论的数学思想.
例题3的解答,学生体会结合题中条件,构造基本图形解决问题.
课堂小结帮助学生理清本节课的知识重点,培养学生归纳、总结的能力.
课 题
相似的基本图形(一)
一、教学目标:
1、进一步认识相似三角形中的基本图形“A”字形、“8”字形,并会运用其进行推理与计算;
2、在解题的过程中体会基本图形的重要性,养成在学习过程中及时总结的习惯;
3、数学思想方法的渗透及一题多解的问题解决激发学生学习数学的兴趣,体验收获的快乐.
二、重点、难点:
重点:应用基本图形解决问题.
难点:构造基本图形解决问题
三、教学过程设计:
问题与情境
师生行为
设计意图
【活动一】
小题得基本图形
问题1:
(1)如图1,当 时,△ABC∽△ADE;
(2)如图2,当 时,△ABC∽△AED;
(3)如图3,当 时,△ABC∽△ACD.
图1 图2
图3 图4
(4)如图4,在Rt△ABC中, ∠ACB=90°, DE⊥AB,则△ ∽△___
(5)如图5,在Rt△ABC中,
∠ACB=90°,CD⊥AB,则图中有____ 对相似三角形.
图5
问题2:
(1)如图1,当AB∥CD时,则△ ∽△ .
(2)如图2,当 时,则△ ∽△ .
图1 图2
【活动二】
应用图形,解决问题
练习:
1.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( ).
A.1个 B.2个 C.3个 D.4个
2. 如图,A、B、C、D是⊙O上的四点,
且弧AB=弧AD,则在此图中,
△ABE∽△ ;△ABE∽△ .
3.如图,在△ABC中,D、E分别是AB,AC上一点,且∠AED =∠B. 若AE=5,AB= 9,CB=6,则ED的长是_________
【活动三】
典型例题,深化提高
例1.如图,CD是Rt△ABC斜边上的高,∠ACB=90°,E为AC的中点,ED交CB的延长线于F.
求证:△CDF∽△DBF.
例2.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O、B、P为顶点的三角形与△ABC相似,则点P的坐标是_____________
例3:如图,△ABC中,D是BC的中点,E 是AB上一点,AD、CE相交于F.若,
求证:.
【活动四】
课堂小结,巩固知识
对今天的基本图形的研究,你有什么收获?
教师出示问题1,学生回答问题.
教师关注学生能否很快地解决问题,并做到有理有据.
教师关注学生能否很快的解决问题.
学生完成问题2
在学生回答的基础上,师生一起对常见的基本图形进行总结.
练习1关注学生能否很快的发现基本图形并迅速的解决问题.
练习2关注学生能否很快的利用圆的知识结合相似的基本图形解决问题.
练习3 关注学生能否很快的发现基本图形并进行问题的转化,从而准确的解决问题.
例1的解答在教师给出问题串的基础上来完成.问题如下:
①你发现图中的基本图形吗?如果有是哪个基本图形?
②由这个基本图形可以得到什么条件?
③我们要证明相似的这对三角形有什么特点?还需要什么条件可以证明相似?
学生在教师的引导下解决问题
例2关注学生能否准确的理解题意再利用相似解决问题.
例题3学生在教师的引导下完成,教师注意观察学生能否较快的构造基本图形解决问题,同时注意观察学生的不同解法.
不同解法的学生展示自己的解题思路.
学生在教师的引导下进行课堂知识归纳.
通过一组小题的解答,加深对“A”字形的理解.
问题2的设置加深学生对“8”字形的理解.
活动二的设置巩固基本图形,加深学生对基本图形的理解.
例1的解决进一步让学生体会到基本图形的重要性.
例2在体会基本图形重要性的同时注意分类讨论的数学思想.
例题3的解答,学生体会结合题中条件,构造基本图形解决问题.
课堂小结帮助学生理清本节课的知识重点,培养学生归纳、总结的能力.
同课章节目录
