九下专题复习8—相似的基本图形2
图片预览



文档简介
课 题
相似的基本图形(二)
一、教学目标:
1、掌握三垂图的结构特征及结论,并会利用这些知识进行推理与计算;
2、经历在运动变化中探索新基本图形的过程,在直观操作活动中提高观察和推理能力,主动探究的习惯,逐步养成良好的学习方法;
3、在了解有三垂图到三等角图的过程中,体会特殊与一般的关系.
二、重点、难点:
重点:在复杂图形中找到基本图形,并能应用基本图形解决问题.
难点:在运动变化的过程中找到不变的关系并证明.
三、教学过程设计:
问题与情境
师生行为
设计意图
【活动一】
复习旧知,引入新知
问题:
①在应用相似三角形解决问题时,常用的基本图形有哪些?
②在双垂图中都有哪些结论呢?
③现在将双垂图作如下的翻折,刚才得到的结论有无改变?
④改变共线三点中中间点的位置,这两个小三角形还相似吗?
⑤如果把这个图形作为基本图形,它的图形特征是什么?
教师提出问题①:
学生思考,并回答:
有“A”字形、“8”字形、双垂图;
教师继续提出问题②:
学生思考,并回答:
有结论:①两对锐角分别相等;
②勾股定理;
③等积变换;
④相似。
通过课件动态演示③④:
学生观察,并回答:
两个小三角形的相似关系未改变;
学生证明,并回答:
两个小三角形依然相似相似。
学生观察图形:
①∠A=∠B=∠DEC=90°
②A、E、B三点共线(三垂足共线)
通过提出问题,对学生的认知前提进行诊断,让学生回顾已有知识,回忆应用基本图形解题的好处,为后续研究较复杂的基本图形做好铺垫.
充分展现变化过程,让学生深切地感受图形之间的联系,同时,又使学生能快速地得出结论.
问题与情境
师生行为
设计意图
【活动二】
应用图形,解决问题
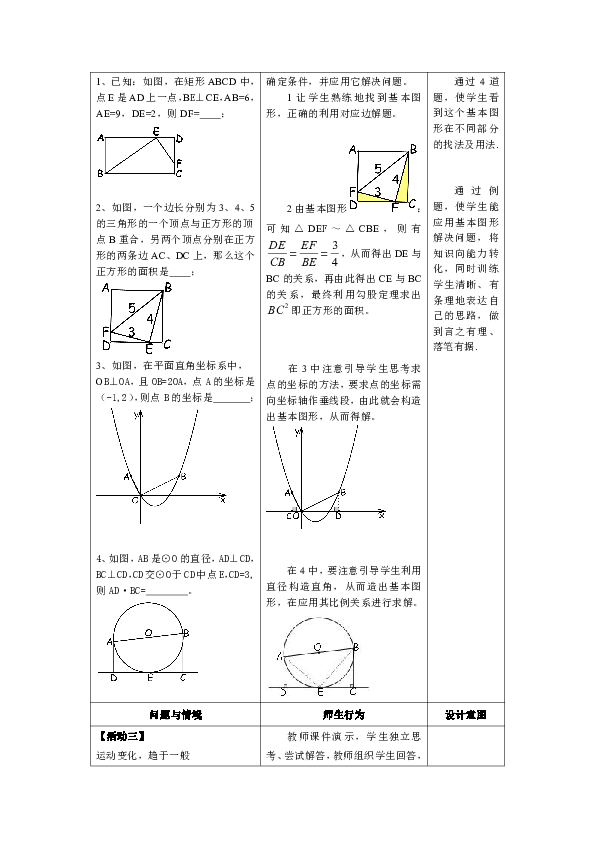
1、已知:如图,在矩形ABCD中,点E是AD上一点,BE⊥CE,AB=6,AE=9,DE=2,则DF= ;
2、如图,一个边长分别为3、4、5的三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AC、DC上,那么这个正方形的面积是 ;
3、如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2),则点B的坐标是 ;
4、如图,AB是⊙O的直径,AD⊥CD,BC⊥CD,CD交⊙O于CD中点E,CD=3,则AD·BC= 。
教师展示例题,学生解答.
注意引导学生寻找基本图形,确定条件,并应用它解决问题。
1让学生熟练地找到基本图形,正确的利用对应边解题。
2由基本图形:
可知△DEF~△CBE,则有,从而得出DE与
BC的关系,再由此得出CE与BC的关系,最终利用勾股定理求出即正方形的面积。
在3中注意引导学生思考求点的坐标的方法,要求点的坐标需向坐标轴作垂线段,由此就会构造出基本图形,从而得解。
在4中,要注意引导学生利用直径构造直角,从而造出基本图形,在应用其比例关系进行求解。
通过4道题,使学生看到这个基本图形在不同部分的找法及用法.
通过例题,使学生能应用基本图形解决问题,将知识向能力转化,同时训练学生清晰、有条理地表达自己的思路,做到言之有理、落笔有据.
问题与情境
师生行为
设计意图
【活动三】
运动变化,趋于一般
问题:
①在刚才的基本图形中保证了有三个相等的角,且都等于90°,那如果保持相等关系不变,但度数不是90°了,还会有相似的结论吗?
②这个基本图形会出现在什么图形中呢?
【活动四】
应用图形,解决问题
1、如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 ;
2、如图,在梯形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与点A、D不重合),且∠BEF=120°,设AE=x,DF=y
求y与x的函数表达式。
教师课件演示,学生独立思考、尝试解答,教师组织学生回答,并说明证题过程.
通过证明发现,图中只要有:①∠A=∠B=∠DEC
②A、E、B三点共线
就能得到两个三角形相似。
观察此图,有∠A=∠B(同一底上的两个角等),可分析出此图可存在于等腰三角形或等腰梯形中。
在1中,通过已知中的60°角,想到等边三角形的60°角,从而出现了三个角等的基本图形。
在2中通过已知中的60°和120°角,想到等腰梯形的性质,利用同旁内角互补及同一底上两角相等,得出三个角等的基本图形。
解题过程学生独立完成,教师巡视,适时指导,实物投影展示学生的解题过程.
通过课件的演示,让学生更直观的看到图形间的联系,并从中找到不变的结论,提高学生的识图能力、推理能力.
两道例题很好的反映了基本图形的应用环境,为发现基本图形又找到一条线索。
问题与情境
师生行为
设计意图
【活动五】
归纳小结
你对今天的基本图形的学习有什么收获?
【活动六】
课堂检测
教师引导学生从解题方法到数学思想去总结归纳。
通过小结,让学生理清本节课的知识结构,掌握图形从特殊到一般的变化规律, 使学生所学的知识形成体系,培养学生归纳、总结的能力.
相似的基本图形(二)
一、教学目标:
1、掌握三垂图的结构特征及结论,并会利用这些知识进行推理与计算;
2、经历在运动变化中探索新基本图形的过程,在直观操作活动中提高观察和推理能力,主动探究的习惯,逐步养成良好的学习方法;
3、在了解有三垂图到三等角图的过程中,体会特殊与一般的关系.
二、重点、难点:
重点:在复杂图形中找到基本图形,并能应用基本图形解决问题.
难点:在运动变化的过程中找到不变的关系并证明.
三、教学过程设计:
问题与情境
师生行为
设计意图
【活动一】
复习旧知,引入新知
问题:
①在应用相似三角形解决问题时,常用的基本图形有哪些?
②在双垂图中都有哪些结论呢?
③现在将双垂图作如下的翻折,刚才得到的结论有无改变?
④改变共线三点中中间点的位置,这两个小三角形还相似吗?
⑤如果把这个图形作为基本图形,它的图形特征是什么?
教师提出问题①:
学生思考,并回答:
有“A”字形、“8”字形、双垂图;
教师继续提出问题②:
学生思考,并回答:
有结论:①两对锐角分别相等;
②勾股定理;
③等积变换;
④相似。
通过课件动态演示③④:
学生观察,并回答:
两个小三角形的相似关系未改变;
学生证明,并回答:
两个小三角形依然相似相似。
学生观察图形:
①∠A=∠B=∠DEC=90°
②A、E、B三点共线(三垂足共线)
通过提出问题,对学生的认知前提进行诊断,让学生回顾已有知识,回忆应用基本图形解题的好处,为后续研究较复杂的基本图形做好铺垫.
充分展现变化过程,让学生深切地感受图形之间的联系,同时,又使学生能快速地得出结论.
问题与情境
师生行为
设计意图
【活动二】
应用图形,解决问题
1、已知:如图,在矩形ABCD中,点E是AD上一点,BE⊥CE,AB=6,AE=9,DE=2,则DF= ;
2、如图,一个边长分别为3、4、5的三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AC、DC上,那么这个正方形的面积是 ;
3、如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2),则点B的坐标是 ;
4、如图,AB是⊙O的直径,AD⊥CD,BC⊥CD,CD交⊙O于CD中点E,CD=3,则AD·BC= 。
教师展示例题,学生解答.
注意引导学生寻找基本图形,确定条件,并应用它解决问题。
1让学生熟练地找到基本图形,正确的利用对应边解题。
2由基本图形:
可知△DEF~△CBE,则有,从而得出DE与
BC的关系,再由此得出CE与BC的关系,最终利用勾股定理求出即正方形的面积。
在3中注意引导学生思考求点的坐标的方法,要求点的坐标需向坐标轴作垂线段,由此就会构造出基本图形,从而得解。
在4中,要注意引导学生利用直径构造直角,从而造出基本图形,在应用其比例关系进行求解。
通过4道题,使学生看到这个基本图形在不同部分的找法及用法.
通过例题,使学生能应用基本图形解决问题,将知识向能力转化,同时训练学生清晰、有条理地表达自己的思路,做到言之有理、落笔有据.
问题与情境
师生行为
设计意图
【活动三】
运动变化,趋于一般
问题:
①在刚才的基本图形中保证了有三个相等的角,且都等于90°,那如果保持相等关系不变,但度数不是90°了,还会有相似的结论吗?
②这个基本图形会出现在什么图形中呢?
【活动四】
应用图形,解决问题
1、如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 ;
2、如图,在梯形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=60°,点E、F分别在AD、DC上(点E与点A、D不重合),且∠BEF=120°,设AE=x,DF=y
求y与x的函数表达式。
教师课件演示,学生独立思考、尝试解答,教师组织学生回答,并说明证题过程.
通过证明发现,图中只要有:①∠A=∠B=∠DEC
②A、E、B三点共线
就能得到两个三角形相似。
观察此图,有∠A=∠B(同一底上的两个角等),可分析出此图可存在于等腰三角形或等腰梯形中。
在1中,通过已知中的60°角,想到等边三角形的60°角,从而出现了三个角等的基本图形。
在2中通过已知中的60°和120°角,想到等腰梯形的性质,利用同旁内角互补及同一底上两角相等,得出三个角等的基本图形。
解题过程学生独立完成,教师巡视,适时指导,实物投影展示学生的解题过程.
通过课件的演示,让学生更直观的看到图形间的联系,并从中找到不变的结论,提高学生的识图能力、推理能力.
两道例题很好的反映了基本图形的应用环境,为发现基本图形又找到一条线索。
问题与情境
师生行为
设计意图
【活动五】
归纳小结
你对今天的基本图形的学习有什么收获?
【活动六】
课堂检测
教师引导学生从解题方法到数学思想去总结归纳。
通过小结,让学生理清本节课的知识结构,掌握图形从特殊到一般的变化规律, 使学生所学的知识形成体系,培养学生归纳、总结的能力.
同课章节目录
