九下专题复习16—二次函数与方程

二次函数与方程
教学分析
教学内容
本课探讨二次函数与方程之间的关系．二次函数从方程的角度看是二元二次方程。虽然学生在初中阶段没有学过二元二次方程，但不难理解二次函数与二元二次方程的等价性，理解二次函数与二元二次方程是同一种模型的不同表现形式，二次函数图像上点的坐标与二元二次方程的解是一一对应关系。构建和发展相互联系的知识体系。通过这节课的学习，使学生可以从函数和方程两个方面去分析问题，使问题的分析过程更加简化。
教学目标
1.经历探索二次函数与二元二次方程的关系的过程，体会方程与函数之间的联系．
2.使学生能够运用二次函数及其图象、性质解决方程问题，提高学生应用数学的意识。
3.构建知识体系间的联系，渗透数形结合思想。
教学重难点
重点：构建知识体系间的联系，渗透数形结合思想。
难点：使学生理解二次函数与二元二次方程之间的联系，能够运用二次函数及其图象、性质去解决方程问题。
教学设计
教学过程
一、创设情境、引入新课
活动一：
这章我们学习的是二次函数，例如我给出的就是一个二次函数。
教师活动：给出函数解析式，引导学生进入课堂情境．
活动二：
问题1：还可以看作是什么？
方程
问题2：你能说出方程的定义吗？
含有未知数的等式叫做方程。
问题3：我们已经学过了方程的命名方式，你能说出是一个什么方程吗？
二元二次方程
教师活动：提出问题，引导学生对问题进行思考．
学生活动：思考回答．
设计意图：通过三个问题，引导学生对方程的角度对二次函数进行重新认识，使学生明白二次函数与二元二次方程是等价的．
活动三：
问题4：二元二次方程有多少组解？
无数组，二元二次方程未知数、，只要其中任一个取定一个具体的值，则另一个就会有具体的数值相对应。
教师活动：引导学生对问题进行分析，帮助学生得到正确结果．
学生活动：主动思考，相互讨论，完成问题．
设计意图：让学生明白当方程中的未知数不唯一时，则方程有无数组解。
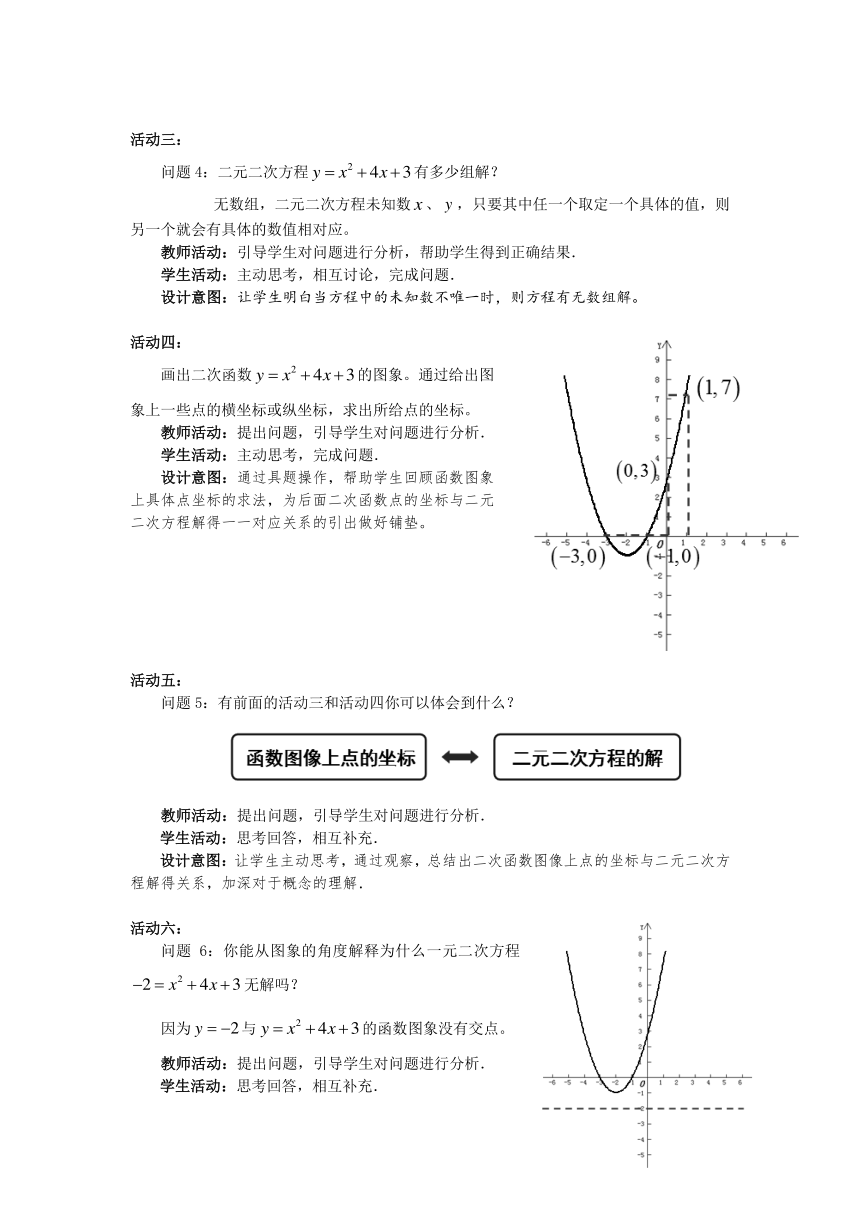
活动四：
画出二次函数的图象。通过给出图象上一些点的横坐标或纵坐标，求出所给点的坐标。
教师活动：提出问题，引导学生对问题进行分析．
学生活动：主动思考，完成问题．
设计意图：通过具题操作，帮助学生回顾函数图象上具体点坐标的求法，为后面二次函数点的坐标与二元二次方程解得一一对应关系的引出做好铺垫。
活动五：
问题5：有前面的活动三和活动四你可以体会到什么？
教师活动：提出问题，引导学生对问题进行分析．
学生活动：思考回答，相互补充．
设计意图：让学生主动思考，通过观察，总结出二次函数图像上点的坐标与二元二次方程解得关系，加深对于概念的理解．
活动六：
问题6：你能从图象的角度解释为什么一元二次方程无解吗？
因为与的函数图象没有交点。
教师活动：提出问题，引导学生对问题进行分析．
学生活动：思考回答，相互补充．
设计意图：通过这个问题，使学生对于二次函数与方程的关系认识的更加清楚，也为后面的练习做好铺垫。
活动七：
梳理知识框图：
教师活动：引导学生梳理知识框图．
学生活动：理解记忆．
二、知识应用，加深理解
活动一：
练习1：把函数图象向下平移3个单位，求平移后的函数图象与轴的交点坐标。
方法一思路：通过向下平移函数的图象，得到平移后的函数图象解析式为，再使函数中的为0，解方程。
方法二思路：问题的求解和函数与的交点横坐标是等价的，所以可以直接求解方程。
教师活动：引导学生对问题进行分析，的帮助学生得到正确结果．
学生活动：主动思考，相互讨论，完成问题．
活动二：
问题7：你觉得这两种方法哪种相对来说更为简单？
教师活动：引导学生对问题进行分析．
学生活动：主动思考，相互讨论，完成问题．
设计意图：通过对于两种方法的比较，加深对于刚学过的知识的认识与应用，而且可以让学生对于问题的认识更加的深刻。
三、能力提升
练习2：若m、n(mA. m练习分析：因讨论一元二次方程的根m、n与系数a、b的大小关系运用根的表达式复杂，不好判断，故把原问题转化为二次函数问题来解决，即求对应的二次函数与直线的交点满足a < b，注意判别式的隐含制约．
解题过程：将方程做变形:
设二次函数，则
抛物线与轴交于两点A（a,0）B（b，0）,
且抛物线开口向上
∵ a < b，
∴ 点A在点B的左侧
∴ 直线 与抛物线有两个交点C,D
∵ m∴ m < a < b< n
教师活动：引导学生对问题进行分析，的帮助学生得到正确结果．
学生活动：主动思考，相互讨论，完成问题．
设计意图：本题是2009北京西城一模试题，运用函数思想讨论方程问题，即直观又简捷,起到了简化解题过程和加快解题速度的作用．用函数图象来解决方程问题起到了以形助数的作用．在讨论一元二次方程的解的个数、解的分布情况等问题时借助函数图象可获得直观简捷的解答．
四、课堂小结
通过本节课的学习，你学会了哪些知识？