九下专题复习1—回顾应用题
图片预览


文档简介
回顾应用题
教学
目标
1. 复习一元二次方程、二次函数、相似三角形、锐角三角函数的应用问题;
2. 通过题组形式,类比归纳基本的解题方法,形成快速解题技能;
3. 培养观察、总结能力,体会化归思想,感受由已知向未知转化的数学思想方法.
教学
重点
感受应用题的本质是相等的关系
教学
难点
根据问题情境寻求解决问题的数学模型
教学阶段
教师活动
学生活动
设计意图
活动一
复习铺垫
我们学习过哪些知识的应用题?
学生思考,并回答:
一元二次方程应用题、二次函数应用题、三角函数应用题、相似三角形应用题
让学生回忆所学过的应用题有哪些?使知识系统化,为下面的复习起到铺垫的作用
活动二
知识梳理
探究本质
活动三
对比归纳
活动四
归纳小结
活动五
作业布置
题组(一)
1.在政府的调控下,一个月内猪肉价格两次大幅下降.由原来每斤16元下调到每斤9元,求平均每次下调的百分率是多少?
解:设平均每次下调的百分率为,则根据题意可列方程为:
16(1-x)2=9
x1=1.75 (舍), x2=0.25
答:每次下调的百分率为25%.
2. 某网站出售一种毛绒兔玩具,试销中发现这种玩具每个获利x元时,一天需销售(60-x)个,如果要使一天出售该种玩具获得最大销售利润,那么每个玩具应获利多少元?
解:设该玩具销售利润为y元.
根据题意,得:y=x(60-x)
= -x2+60x
当x= 30时, y= 900
答:要使一天出售该玩具获得最大销售利润,每个玩具应获利30元。
问题:解上面两道题的关键是什么?
引导学生回答:找相等的关系
例1:某广告公司设计一幅周长为12米的矩形广告牌,
(1)若矩形的面积为5平方米时,求矩形的长和宽。
(2) 若广告设计费为每平方米1000元,请你设计一个方案,使获得的设计费最多,并求出这个费用。
解:(1)设矩形一边长为米,所以矩形的宽为(6-)米。
根据题意,x(6-x)=5
x1=1 , x2=5
答:矩形的长为5米,宽为1米。
(2)设矩形的面积为s,由(1)知
所以,当时,S取最大值为9。
9×1000=9000(元)。
所以广告牌设计成正方形时,可获得设计费最多,此时设计费为9000(元)。
问题:
(1)问题一是什么类型的应用题?
(2)问题二是什么类型的应用题?
(3)在解题思路上有什么相同点和不同点?
小结:
相同点:
将生活中的问题转化成数学问题;
构建数学模型,列代数方程(找相等的关系);
数学模型的解;
实际问题的解。
不同点:
对一个未知数得出答案;利用两个未知数得出答案。
题组(二)
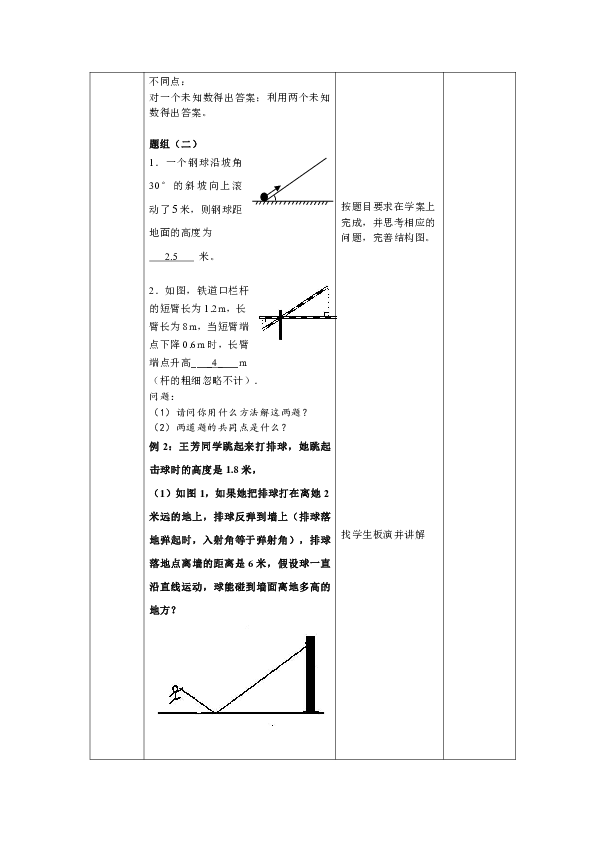
1.一个钢球沿坡角30°的斜坡向上滚动了米,则钢球距地面的高度为
2.5 米。
2.如图,铁道口栏杆
的短臂长为1.2m,长
臂长为8m,当短臂端
点下降0.6m时,长臂
端点升高____4____m
(杆的粗细忽略不计).
问题:
(1)请问你用什么方法解这两题?
(2)两道题的共同点是什么?
例2:王芳同学跳起来打排球,她跳起击球时的高度是1.8米,
(1)如图1,如果她把排球打在离她2米远的地上,排球反弹到墙上(排球落地弹起时,入射角等于弹射角),排球落地点离墙的距离是6米,假设球一直沿直线运动,球能碰到墙面离地多高的地方?
解:过点A作AB⊥BD于点B.
依题意可得∠AEB=∠CEB,∠B=∠D=90°
∴ AEB∽ CED
AB:CD=BE:ED
∴CD=5.4米
答:球能碰到墙面离地5.4米高的地方
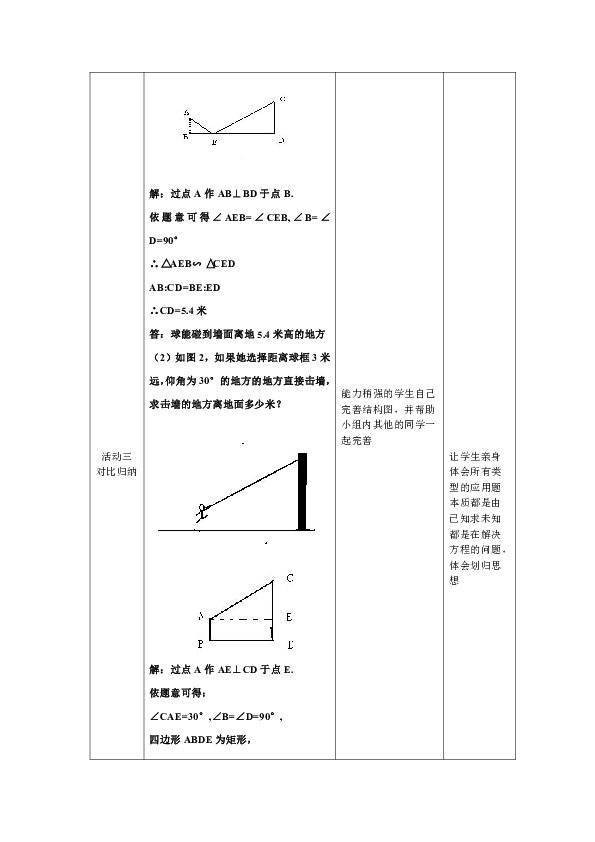
(2)如图2,如果她选择距离球框3米远,仰角为30°的地方的地方直接击墙,求击墙的地方离地面多少米?
解:过点A作AE⊥CD于点E.
依题意可得:
∠CAE=30°,∠B=∠D=90°,
四边形ABDE为矩形,
∴AE=BD=3米
在Rt CAE中,
∠CEA=90°
tan∠CAE=30°,
∴CE=
解题后思考:
题组(一)和题组(二)用到了哪些知识?
他们的本质是什么?
题组(一)和题组(二)的共同点和不同点是什么?
他们有什么联系?
1. 某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个。
(1)当销售的利润为8000元时,篮球的销售价为多少元?
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请你求出最大利润,此时篮球的售价应定为多少元?
2. 如图,甲、乙两船同时从港口O出发,甲船以16海里/时的速度向东偏西30°方向航行,乙船向西偏南60°方向航行,航行了两小时,甲船到达A处并观测到B 处的乙船恰好在其正西方向,求乙船的速度(精确到0.1海里/时).
学生独立完成1.2,并小组合作完成结构图
思考问题,并回答
根据所学知识,思考,选择适当的方法来解应用题,在学案上按要求完成题目。
学生完成求解后,注意要回到生活实际中去
思考问题,完成结构图
根据结构图,思考问题,体会初中应用题之间的联系。
按题目要求在学案上完成,并思考相应的问题,完善结构图。
找学生板演并讲解
能力稍强的学生自己完善结构图,并帮助小组内其他的同学一起完善
巩固本节课所学的知识
体会复杂的解决应用题的本质是:找相等的关系。
让学生经历动手操作、观察对比,发现联系.使学生
体验方程应用题与函数应用题之间的联系,降低函数应用题的难度。
让学生亲身体会所有类型的应用题本质都是由已知求未知都是在解决方程的问题,体会划归思想
教学
目标
1. 复习一元二次方程、二次函数、相似三角形、锐角三角函数的应用问题;
2. 通过题组形式,类比归纳基本的解题方法,形成快速解题技能;
3. 培养观察、总结能力,体会化归思想,感受由已知向未知转化的数学思想方法.
教学
重点
感受应用题的本质是相等的关系
教学
难点
根据问题情境寻求解决问题的数学模型
教学阶段
教师活动
学生活动
设计意图
活动一
复习铺垫
我们学习过哪些知识的应用题?
学生思考,并回答:
一元二次方程应用题、二次函数应用题、三角函数应用题、相似三角形应用题
让学生回忆所学过的应用题有哪些?使知识系统化,为下面的复习起到铺垫的作用
活动二
知识梳理
探究本质
活动三
对比归纳
活动四
归纳小结
活动五
作业布置
题组(一)
1.在政府的调控下,一个月内猪肉价格两次大幅下降.由原来每斤16元下调到每斤9元,求平均每次下调的百分率是多少?
解:设平均每次下调的百分率为,则根据题意可列方程为:
16(1-x)2=9
x1=1.75 (舍), x2=0.25
答:每次下调的百分率为25%.
2. 某网站出售一种毛绒兔玩具,试销中发现这种玩具每个获利x元时,一天需销售(60-x)个,如果要使一天出售该种玩具获得最大销售利润,那么每个玩具应获利多少元?
解:设该玩具销售利润为y元.
根据题意,得:y=x(60-x)
= -x2+60x
当x= 30时, y= 900
答:要使一天出售该玩具获得最大销售利润,每个玩具应获利30元。
问题:解上面两道题的关键是什么?
引导学生回答:找相等的关系
例1:某广告公司设计一幅周长为12米的矩形广告牌,
(1)若矩形的面积为5平方米时,求矩形的长和宽。
(2) 若广告设计费为每平方米1000元,请你设计一个方案,使获得的设计费最多,并求出这个费用。
解:(1)设矩形一边长为米,所以矩形的宽为(6-)米。
根据题意,x(6-x)=5
x1=1 , x2=5
答:矩形的长为5米,宽为1米。
(2)设矩形的面积为s,由(1)知
所以,当时,S取最大值为9。
9×1000=9000(元)。
所以广告牌设计成正方形时,可获得设计费最多,此时设计费为9000(元)。
问题:
(1)问题一是什么类型的应用题?
(2)问题二是什么类型的应用题?
(3)在解题思路上有什么相同点和不同点?
小结:
相同点:
将生活中的问题转化成数学问题;
构建数学模型,列代数方程(找相等的关系);
数学模型的解;
实际问题的解。
不同点:
对一个未知数得出答案;利用两个未知数得出答案。
题组(二)
1.一个钢球沿坡角30°的斜坡向上滚动了米,则钢球距地面的高度为
2.5 米。
2.如图,铁道口栏杆
的短臂长为1.2m,长
臂长为8m,当短臂端
点下降0.6m时,长臂
端点升高____4____m
(杆的粗细忽略不计).
问题:
(1)请问你用什么方法解这两题?
(2)两道题的共同点是什么?
例2:王芳同学跳起来打排球,她跳起击球时的高度是1.8米,
(1)如图1,如果她把排球打在离她2米远的地上,排球反弹到墙上(排球落地弹起时,入射角等于弹射角),排球落地点离墙的距离是6米,假设球一直沿直线运动,球能碰到墙面离地多高的地方?
解:过点A作AB⊥BD于点B.
依题意可得∠AEB=∠CEB,∠B=∠D=90°
∴ AEB∽ CED
AB:CD=BE:ED
∴CD=5.4米
答:球能碰到墙面离地5.4米高的地方
(2)如图2,如果她选择距离球框3米远,仰角为30°的地方的地方直接击墙,求击墙的地方离地面多少米?
解:过点A作AE⊥CD于点E.
依题意可得:
∠CAE=30°,∠B=∠D=90°,
四边形ABDE为矩形,
∴AE=BD=3米
在Rt CAE中,
∠CEA=90°
tan∠CAE=30°,
∴CE=
解题后思考:
题组(一)和题组(二)用到了哪些知识?
他们的本质是什么?
题组(一)和题组(二)的共同点和不同点是什么?
他们有什么联系?
1. 某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个。
(1)当销售的利润为8000元时,篮球的销售价为多少元?
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请你求出最大利润,此时篮球的售价应定为多少元?
2. 如图,甲、乙两船同时从港口O出发,甲船以16海里/时的速度向东偏西30°方向航行,乙船向西偏南60°方向航行,航行了两小时,甲船到达A处并观测到B 处的乙船恰好在其正西方向,求乙船的速度(精确到0.1海里/时).
学生独立完成1.2,并小组合作完成结构图
思考问题,并回答
根据所学知识,思考,选择适当的方法来解应用题,在学案上按要求完成题目。
学生完成求解后,注意要回到生活实际中去
思考问题,完成结构图
根据结构图,思考问题,体会初中应用题之间的联系。
按题目要求在学案上完成,并思考相应的问题,完善结构图。
找学生板演并讲解
能力稍强的学生自己完善结构图,并帮助小组内其他的同学一起完善
巩固本节课所学的知识
体会复杂的解决应用题的本质是:找相等的关系。
让学生经历动手操作、观察对比,发现联系.使学生
体验方程应用题与函数应用题之间的联系,降低函数应用题的难度。
让学生亲身体会所有类型的应用题本质都是由已知求未知都是在解决方程的问题,体会划归思想
同课章节目录
