九下专题复习17—动手操作
图片预览

文档简介
课题
动手操作(1)
一、教学目标:
1、掌握在平移、翻折等几何变换中的一些特殊位置点在动手操作题中的分类作用。
2、经历简单几何变换中的特殊位置点的探究过程,在直观操作活动中发展初步的合理推理能力,主动探究习惯和解决完问题后的反思和总结习惯;
3、在探究运动中的特殊静止状态对问题进行分类讨论的过程中,体会特殊与一般的关系,渗透集合的思想,培养学生辨证唯物主义观点.
二、重点、难点:
重点:会在平移、翻折等几何变换中准确找出图形的特殊位置关系进行分类讨论来解决问题。
难点:在复杂图形中探究出几何变换中特殊静止点。
三、教学流程安排:
活动流程图
活动内容和目的
活动一 温故知新
活动二 探究新知,总结规律
活动三 理解特殊点(分界点)法,初步解决问题。
活动四 分类的灵活应用
活动五 拓展
活动六 归纳小结
通过复习圆和圆位置关系的问题,初步感受运动中的特殊静止位置,为后续研究做好铺垫.
通过自主探索、合作交流,感受运动中的特殊静止点来进行分类讨论的方法。
简单的应用训练
学生在正三角形中探究讨论如何利用利用等边三角形的中点解决问题。
学生在矩形中探究移动中的特殊静止点来解决几何最大值问题。
理清本节课的知识结构,培养学生归纳、总结的能力.
四、教学过程设计
问题与情境
师生行为
设计意图
【活动一】温故知新
问题:
(1).已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是 。
.
【活动二】探究新知,总结规律
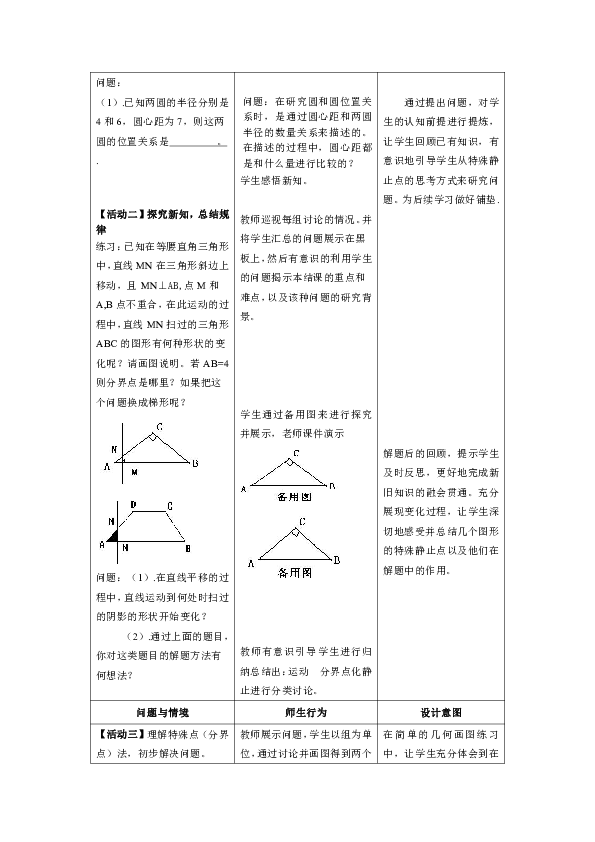
练习:已知在等腰直角三角形中,直线MN在三角形斜边上移动,且MN⊥AB,点M和A,B点不重合,在此运动的过程中,直线MN扫过的三角形ABC的图形有何种形状的变化呢?请画图说明。若AB=4则分界点是哪里?如果把这个问题换成梯形呢?
问题:(1).在直线平移的过程中,直线运动到何处时扫过的阴影的形状开始变化?
(2).通过上面的题目,你对这类题目的解题方法有何想法?
问题:在研究圆和圆位置关系时,是通过圆心距和两圆半径的数量关系来描述的。在描述的过程中,圆心距都是和什么量进行比较的?
学生感悟新知。
教师巡视每组讨论的情况。并将学生汇总的问题展示在黑板上,然后有意识的利用学生的问题揭示本结课的重点和难点,以及该种问题的研究背景。
学生通过备用图来进行探究并展示,老师课件演示
教师有意识引导学生进行归纳总结出:运动 分界点化静止进行分类讨论。
通过提出问题,对学生的认知前提进行提炼,让学生回顾已有知识,有意识地引导学生从特殊静止点的思考方式来研究问题。为后续学习做好铺垫.
解题后的回顾,提示学生及时反思,更好地完成新旧知识的融会贯通。充分展现变化过程,让学生深切地感受并总结几个图形的特殊静止点以及他们在解题中的作用。
问题与情境
师生行为
设计意图
【活动三】理解特殊点(分界点)法,初步解决问题。
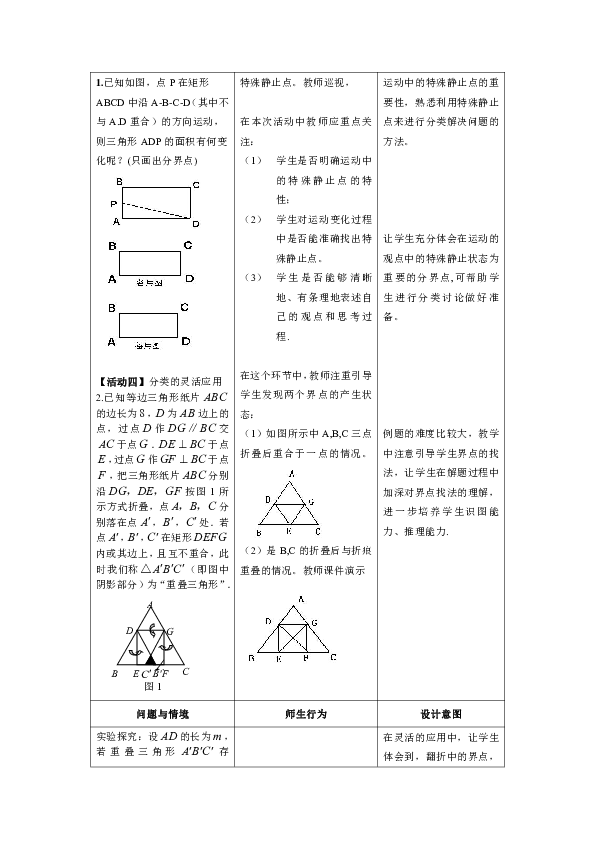
1.已知如图,点P在矩形ABCD中沿A-B-C-D(其中不与A.D重合)的方向运动,则三角形ADP的面积有何变化呢?(只画出分界点)
【活动四】分类的灵活应用
2.已知等边三角形纸片的边长为,为边上的点,过点作交于点.于点,过点作于点,把三角形纸片分别沿按图1所示方式折叠,点分别落在点,,处.若点,,在矩形内或其边上,且互不重合,此时我们称(即图中阴影部分)为“重叠三角形”.
教师展示问题,学生以组为单位,通过讨论并画图得到两个特殊静止点。教师巡视,
在本次活动中教师应重点关注:
学生是否明确运动中的特殊静止点的特性;
学生对运动变化过程中是否能准确找出特殊静止点。
学生是否能够清晰地、有条理地表述自己的观点和思考过程.
在这个环节中,教师注重引导学生发现两个界点的产生状态:
(1)如图所示中A,B,C三点折叠后重合于一点的情况。
(2)是B,C的折叠后与折痕重叠的情况。教师课件演示
在简单的几何画图练习中,让学生充分体会到在运动中的特殊静止点的重要性,熟悉利用特殊静止点来进行分类解决问题的方法。
让学生充分体会在运动的观点中的特殊静止状态为重要的分界点,可帮助学生进行分类讨论做好准备。
例题的难度比较大,教学中注意引导学生界点的找法,让学生在解题过程中加深对界点找法的理解,进一步培养学生识图能力、推理能力.
问题与情境
师生行为
设计意图
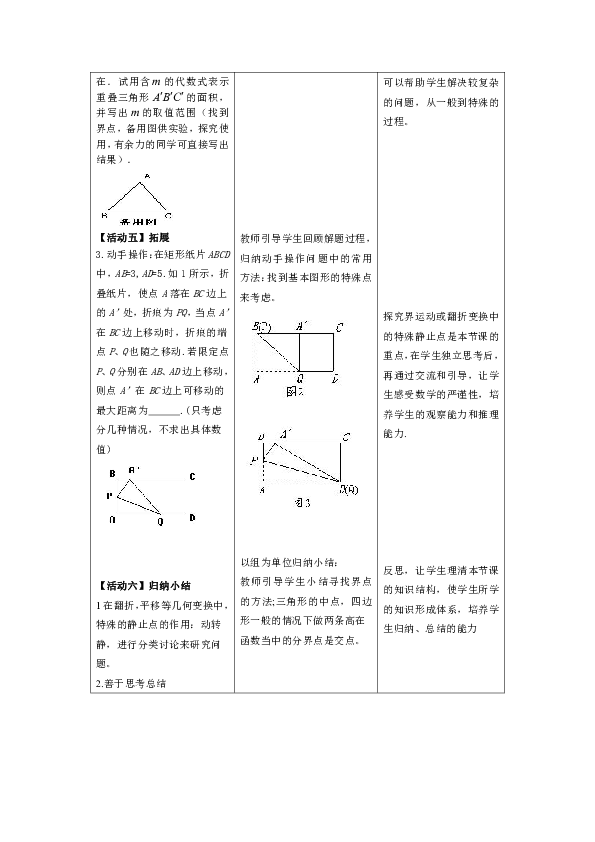
实验探究:设的长为,若重叠三角形存在.试用含的代数式表示重叠三角形的面积,并写出的取值范围(找到界点,备用图供实验,探究使用,有余力的同学可直接写出结果).
【活动五】拓展
3.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如1所示,折叠纸片,使点A落在BC边上的A’处,折痕为PQ,当点A’在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A’在BC边上可移动的最大距离为 .(只考虑分几种情况,不求出具体数值)
【活动六】归纳小结
1在翻折,平移等几何变换中,特殊的静止点的作用:动转静,进行分类讨论来研究问题。
2.善于思考总结
教师引导学生回顾解题过程,归纳动手操作问题中的常用方法:找到基本图形的特殊点来考虑。
以组为单位归纳小结:
教师引导学生小结寻找界点的方法;三角形的中点,四边形一般的情况下做两条高在
函数当中的分界点是交点。
在灵活的应用中,让学生体会到,翻折中的界点,可以帮助学生解决较复杂的问题,从一般到特殊的过程。
探究界运动或翻折变换中的特殊静止点是本节课的重点,在学生独立思考后,再通过交流和引导,让学生感受数学的严谨性,培养学生的观察能力和推理能力.
反思,让学生理清本节课的知识结构,使学生所学的知识形成体系,培养学生归纳、总结的能力
动手操作(1)
一、教学目标:
1、掌握在平移、翻折等几何变换中的一些特殊位置点在动手操作题中的分类作用。
2、经历简单几何变换中的特殊位置点的探究过程,在直观操作活动中发展初步的合理推理能力,主动探究习惯和解决完问题后的反思和总结习惯;
3、在探究运动中的特殊静止状态对问题进行分类讨论的过程中,体会特殊与一般的关系,渗透集合的思想,培养学生辨证唯物主义观点.
二、重点、难点:
重点:会在平移、翻折等几何变换中准确找出图形的特殊位置关系进行分类讨论来解决问题。
难点:在复杂图形中探究出几何变换中特殊静止点。
三、教学流程安排:
活动流程图
活动内容和目的
活动一 温故知新
活动二 探究新知,总结规律
活动三 理解特殊点(分界点)法,初步解决问题。
活动四 分类的灵活应用
活动五 拓展
活动六 归纳小结
通过复习圆和圆位置关系的问题,初步感受运动中的特殊静止位置,为后续研究做好铺垫.
通过自主探索、合作交流,感受运动中的特殊静止点来进行分类讨论的方法。
简单的应用训练
学生在正三角形中探究讨论如何利用利用等边三角形的中点解决问题。
学生在矩形中探究移动中的特殊静止点来解决几何最大值问题。
理清本节课的知识结构,培养学生归纳、总结的能力.
四、教学过程设计
问题与情境
师生行为
设计意图
【活动一】温故知新
问题:
(1).已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是 。
.
【活动二】探究新知,总结规律
练习:已知在等腰直角三角形中,直线MN在三角形斜边上移动,且MN⊥AB,点M和A,B点不重合,在此运动的过程中,直线MN扫过的三角形ABC的图形有何种形状的变化呢?请画图说明。若AB=4则分界点是哪里?如果把这个问题换成梯形呢?
问题:(1).在直线平移的过程中,直线运动到何处时扫过的阴影的形状开始变化?
(2).通过上面的题目,你对这类题目的解题方法有何想法?
问题:在研究圆和圆位置关系时,是通过圆心距和两圆半径的数量关系来描述的。在描述的过程中,圆心距都是和什么量进行比较的?
学生感悟新知。
教师巡视每组讨论的情况。并将学生汇总的问题展示在黑板上,然后有意识的利用学生的问题揭示本结课的重点和难点,以及该种问题的研究背景。
学生通过备用图来进行探究并展示,老师课件演示
教师有意识引导学生进行归纳总结出:运动 分界点化静止进行分类讨论。
通过提出问题,对学生的认知前提进行提炼,让学生回顾已有知识,有意识地引导学生从特殊静止点的思考方式来研究问题。为后续学习做好铺垫.
解题后的回顾,提示学生及时反思,更好地完成新旧知识的融会贯通。充分展现变化过程,让学生深切地感受并总结几个图形的特殊静止点以及他们在解题中的作用。
问题与情境
师生行为
设计意图
【活动三】理解特殊点(分界点)法,初步解决问题。
1.已知如图,点P在矩形ABCD中沿A-B-C-D(其中不与A.D重合)的方向运动,则三角形ADP的面积有何变化呢?(只画出分界点)
【活动四】分类的灵活应用
2.已知等边三角形纸片的边长为,为边上的点,过点作交于点.于点,过点作于点,把三角形纸片分别沿按图1所示方式折叠,点分别落在点,,处.若点,,在矩形内或其边上,且互不重合,此时我们称(即图中阴影部分)为“重叠三角形”.
教师展示问题,学生以组为单位,通过讨论并画图得到两个特殊静止点。教师巡视,
在本次活动中教师应重点关注:
学生是否明确运动中的特殊静止点的特性;
学生对运动变化过程中是否能准确找出特殊静止点。
学生是否能够清晰地、有条理地表述自己的观点和思考过程.
在这个环节中,教师注重引导学生发现两个界点的产生状态:
(1)如图所示中A,B,C三点折叠后重合于一点的情况。
(2)是B,C的折叠后与折痕重叠的情况。教师课件演示
在简单的几何画图练习中,让学生充分体会到在运动中的特殊静止点的重要性,熟悉利用特殊静止点来进行分类解决问题的方法。
让学生充分体会在运动的观点中的特殊静止状态为重要的分界点,可帮助学生进行分类讨论做好准备。
例题的难度比较大,教学中注意引导学生界点的找法,让学生在解题过程中加深对界点找法的理解,进一步培养学生识图能力、推理能力.
问题与情境
师生行为
设计意图
实验探究:设的长为,若重叠三角形存在.试用含的代数式表示重叠三角形的面积,并写出的取值范围(找到界点,备用图供实验,探究使用,有余力的同学可直接写出结果).
【活动五】拓展
3.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如1所示,折叠纸片,使点A落在BC边上的A’处,折痕为PQ,当点A’在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A’在BC边上可移动的最大距离为 .(只考虑分几种情况,不求出具体数值)
【活动六】归纳小结
1在翻折,平移等几何变换中,特殊的静止点的作用:动转静,进行分类讨论来研究问题。
2.善于思考总结
教师引导学生回顾解题过程,归纳动手操作问题中的常用方法:找到基本图形的特殊点来考虑。
以组为单位归纳小结:
教师引导学生小结寻找界点的方法;三角形的中点,四边形一般的情况下做两条高在
函数当中的分界点是交点。
在灵活的应用中,让学生体会到,翻折中的界点,可以帮助学生解决较复杂的问题,从一般到特殊的过程。
探究界运动或翻折变换中的特殊静止点是本节课的重点,在学生独立思考后,再通过交流和引导,让学生感受数学的严谨性,培养学生的观察能力和推理能力.
反思,让学生理清本节课的知识结构,使学生所学的知识形成体系,培养学生归纳、总结的能力
同课章节目录
