5.1.1相交线课件2021--2022学年人教版七年级数学下册(共25张ppt)
文档属性
| 名称 | 5.1.1相交线课件2021--2022学年人教版七年级数学下册(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
5.1.1 相交线
1.借助两直线相交所形成的角初步理解邻补角、对顶角的概念.
2.会根据邻补角、对顶角的性质去求一个角的度数.
3.掌握邻补角与对顶角的性质,并能运用它们解决简单实际问题.
学习目标
重点:理解邻补角和对顶角的概念.
难点:探索相交线对顶角之间的关系.
重难点
新课导入
∠1,∠2,∠3,∠4
两条直线相交,形成的小于平角的角有哪几个?
1
2
3
4
B
A
C
D
O
将这些角两两相配能得到几对角?
这些角有什么位置和数量关系?
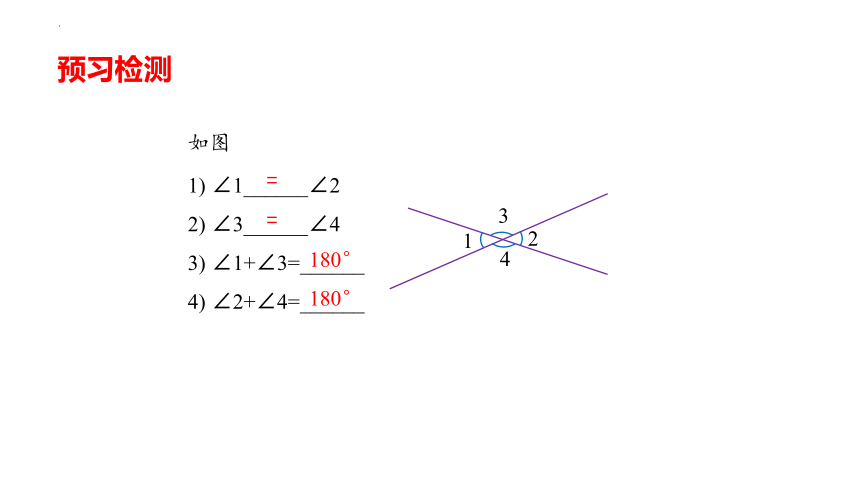
课前预习
1
2
3
4
1) ∠1______∠2
2) ∠3______∠4
3) ∠1+∠3=______
4) ∠2+∠4=______
=
=
180°
180°
预习检测
如图
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片. 如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题。
观察右图,注意剪刀剪开布片过程中有关角的变化.
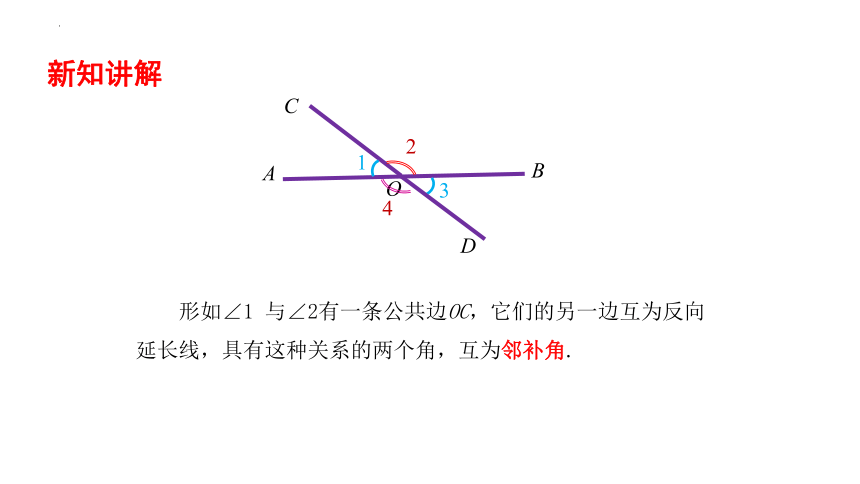
新知讲解
1
2
3
4
A
B
C
D
形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
新知讲解
(
O
A
B
C
D
1
3
2
)
(
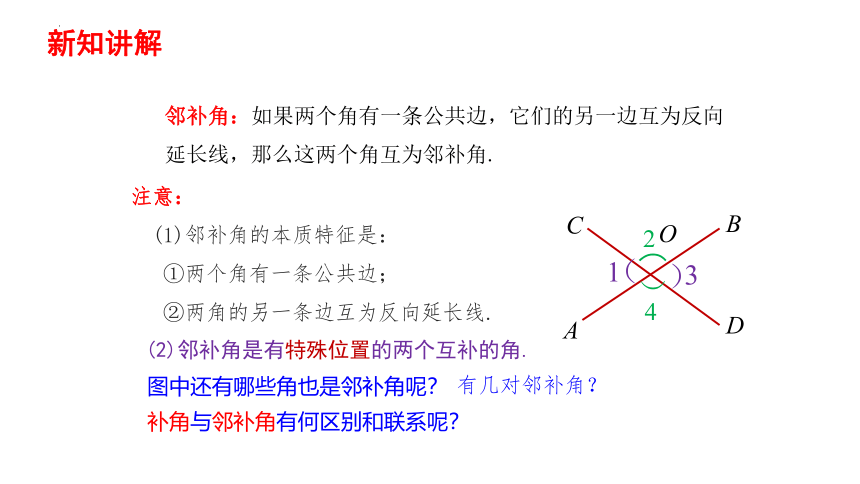
注意:
(1)邻补角的本质特征是:
①两个角有一条公共边;
②两角的另一条边互为反向延长线.
(2)邻补角是有特殊位置的两个互补的角.
图中还有哪些角也是邻补角呢?
有几对邻补角?
补角与邻补角有何区别和联系呢?
(
4
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
新知讲解
1
2
3
4
A
B
C
D
O
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中还有哪些角也是对顶角呢?
新知讲解
对顶角:如果两个角有一个公共点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
(1)辨认对顶角的要领
一看是不是两条直线相交所成的角;
二看是不是有公共顶点;
三看是不是没有公共边.
A
B
C
D
1
3
2
)
(
)
(
∠1与∠3在数量上又有什么关系呢?
(2)对顶角是成对存在的,它们是互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角.
注意:
新知讲解
对顶角的性质:对顶角相等.
已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3, ∠2=∠4
∴ ∠1+∠2=180°,∠3+∠2 =180°
∴∠1=∠3
同理可得:∠2=∠4
证明:∵直线AB与CD相交于O点,
A
B
C
D
O
1
3
2
4
新知讲解
名称 特征 性质 相同点 不同点
对顶角
邻补角 1.两条直线相交而成的角
2.有一个公共顶点
3.没有公共边
1.两条直线相交而成的角
2.有一个公共顶点
3.有一条公共边
对顶角
相等
邻补角
互补
由两条直线相交而成的角,都有一个公共顶点,
他们都成对出现
1.对顶角没有公共边,邻补角有一条公共边.
2.两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个.
归纳总结
例1 如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°
=140°;
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
(
a
b
)
(
1
3
4
)
2
例题分析
解答此类题目,找准对顶角和邻补角,利用对顶角相等,邻补角互补进行解答即可.
方法总结
如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
∵∠BOF=∠2 (对顶角相等),
解:∵∠1=40°, ∠BOC=110° (已知),
∴∠BOF=∠BOC-∠1 =110°-40°=70°.
∴∠2=70° (等量代换).
练习
如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3
C.∠2和∠4 D.∠2和∠5
A
练习
1.如图,三条直线相交于点O,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
C
4
∠1 = ∠4
∠1+∠2+∠3 = ∠4+∠2+∠3=180°
随堂检测
2.如图,三条直线AB,CD,EF相交于点O,若∠BOE=4∠BOD,∠AOE=100°,则∠AOC等于( )
A.30° B.20° C.15° D.10°
B
100°
80°
20°
20°
随堂检测
3.如图,AB和CD相交于点O.
(1)若∠1+∠3=50°,则∠3=____;
(2)若∠1∶∠2=2∶3,则∠3=____;
(3)若∠2-∠3=70°,则∠3=____.
25°
72°
55°
∠1=∠3 =25°
∠1+∠2 =180°
∠3 = ∠1 =180°÷5×2 = 72°
∠2+∠3 =180°
2∠3=110°
∠3=55°
随堂检测
4.如图,∠AOC和∠BOC是邻补角,OE,OF分别平分∠AOC和∠BOC,则∠EOF的度数为____.
90°
1
2
3
4
∠1=∠2
∠3=∠4
∠1+∠2+∠3+∠4 =180°
2(∠1+∠4)=180°
∠1+∠4=90°
随堂检测
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
5.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
A
B
C
D
N
M
O
解:(1)∵ ∠AOC+∠AOD=∠AOD+∠BOD=180°,
∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
随堂检测
故∠DON的余角为:∠DOM,∠BOM.
5.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(2)写出∠DON的余角.
A
B
C
D
N
M
O
解:(2)由∠DON+∠DOM=∠MON=90°知∠DOM为∠DON的余角,
∵ ∠DON+∠DOM=90°,∠DOM=∠MOB,
∴ ∠DON+∠BOM=90°,
随堂检测
课堂小结
名称 特征 性质 相同点 不同点
对顶角
邻补角 1.两条直线相交而成的角
2.有一个公共顶点
3.没有公共边
1.两条直线相交而成的角
2.有一个公共顶点
3.有一条公共边
对顶角
相等
邻补角
互补
由两条直线相交而成的角,都有一个公共顶点,
他们都成对出现
1.对顶角没有公共边,邻补角有一条公共边.
2.两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个.
5.1.1 相交线
1.借助两直线相交所形成的角初步理解邻补角、对顶角的概念.
2.会根据邻补角、对顶角的性质去求一个角的度数.
3.掌握邻补角与对顶角的性质,并能运用它们解决简单实际问题.
学习目标
重点:理解邻补角和对顶角的概念.
难点:探索相交线对顶角之间的关系.
重难点
新课导入
∠1,∠2,∠3,∠4
两条直线相交,形成的小于平角的角有哪几个?
1
2
3
4
B
A
C
D
O
将这些角两两相配能得到几对角?
这些角有什么位置和数量关系?
课前预习
1
2
3
4
1) ∠1______∠2
2) ∠3______∠4
3) ∠1+∠3=______
4) ∠2+∠4=______
=
=
180°
180°
预习检测
如图
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片. 如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题。
观察右图,注意剪刀剪开布片过程中有关角的变化.
新知讲解
1
2
3
4
A
B
C
D
形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
新知讲解
(
O
A
B
C
D
1
3
2
)
(
注意:
(1)邻补角的本质特征是:
①两个角有一条公共边;
②两角的另一条边互为反向延长线.
(2)邻补角是有特殊位置的两个互补的角.
图中还有哪些角也是邻补角呢?
有几对邻补角?
补角与邻补角有何区别和联系呢?
(
4
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
新知讲解
1
2
3
4
A
B
C
D
O
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中还有哪些角也是对顶角呢?
新知讲解
对顶角:如果两个角有一个公共点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.
(1)辨认对顶角的要领
一看是不是两条直线相交所成的角;
二看是不是有公共顶点;
三看是不是没有公共边.
A
B
C
D
1
3
2
)
(
)
(
∠1与∠3在数量上又有什么关系呢?
(2)对顶角是成对存在的,它们是互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角.
注意:
新知讲解
对顶角的性质:对顶角相等.
已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3, ∠2=∠4
∴ ∠1+∠2=180°,∠3+∠2 =180°
∴∠1=∠3
同理可得:∠2=∠4
证明:∵直线AB与CD相交于O点,
A
B
C
D
O
1
3
2
4
新知讲解
名称 特征 性质 相同点 不同点
对顶角
邻补角 1.两条直线相交而成的角
2.有一个公共顶点
3.没有公共边
1.两条直线相交而成的角
2.有一个公共顶点
3.有一条公共边
对顶角
相等
邻补角
互补
由两条直线相交而成的角,都有一个公共顶点,
他们都成对出现
1.对顶角没有公共边,邻补角有一条公共边.
2.两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个.
归纳总结
例1 如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°
=140°;
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
(
a
b
)
(
1
3
4
)
2
例题分析
解答此类题目,找准对顶角和邻补角,利用对顶角相等,邻补角互补进行解答即可.
方法总结
如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
∵∠BOF=∠2 (对顶角相等),
解:∵∠1=40°, ∠BOC=110° (已知),
∴∠BOF=∠BOC-∠1 =110°-40°=70°.
∴∠2=70° (等量代换).
练习
如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3
C.∠2和∠4 D.∠2和∠5
A
练习
1.如图,三条直线相交于点O,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
C
4
∠1 = ∠4
∠1+∠2+∠3 = ∠4+∠2+∠3=180°
随堂检测
2.如图,三条直线AB,CD,EF相交于点O,若∠BOE=4∠BOD,∠AOE=100°,则∠AOC等于( )
A.30° B.20° C.15° D.10°
B
100°
80°
20°
20°
随堂检测
3.如图,AB和CD相交于点O.
(1)若∠1+∠3=50°,则∠3=____;
(2)若∠1∶∠2=2∶3,则∠3=____;
(3)若∠2-∠3=70°,则∠3=____.
25°
72°
55°
∠1=∠3 =25°
∠1+∠2 =180°
∠3 = ∠1 =180°÷5×2 = 72°
∠2+∠3 =180°
2∠3=110°
∠3=55°
随堂检测
4.如图,∠AOC和∠BOC是邻补角,OE,OF分别平分∠AOC和∠BOC,则∠EOF的度数为____.
90°
1
2
3
4
∠1=∠2
∠3=∠4
∠1+∠2+∠3+∠4 =180°
2(∠1+∠4)=180°
∠1+∠4=90°
随堂检测
∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;
5.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
A
B
C
D
N
M
O
解:(1)∵ ∠AOC+∠AOD=∠AOD+∠BOD=180°,
∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
随堂检测
故∠DON的余角为:∠DOM,∠BOM.
5.如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(2)写出∠DON的余角.
A
B
C
D
N
M
O
解:(2)由∠DON+∠DOM=∠MON=90°知∠DOM为∠DON的余角,
∵ ∠DON+∠DOM=90°,∠DOM=∠MOB,
∴ ∠DON+∠BOM=90°,
随堂检测
课堂小结
名称 特征 性质 相同点 不同点
对顶角
邻补角 1.两条直线相交而成的角
2.有一个公共顶点
3.没有公共边
1.两条直线相交而成的角
2.有一个公共顶点
3.有一条公共边
对顶角
相等
邻补角
互补
由两条直线相交而成的角,都有一个公共顶点,
他们都成对出现
1.对顶角没有公共边,邻补角有一条公共边.
2.两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个.
