鲁教版(五四学制)八年级下册 6.1 菱形的性质与判定 导学案无答案
文档属性
| 名称 | 鲁教版(五四学制)八年级下册 6.1 菱形的性质与判定 导学案无答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 43.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:07:41 | ||
图片预览

文档简介
八年级数学导学案 第___周第___课时
课题 6.1 菱形的性质与判定(3) 课 型 新授课 主备人
备课组审核 八年级备课组 级部审核 学生姓名
教师寄语 做好自己,才能成就自己。
学习目标 正确说出菱形的判定方法。会证明菱形的两种判定方法应用菱形的判定方法判定四边形是平行四边形,并解决相关的问题。
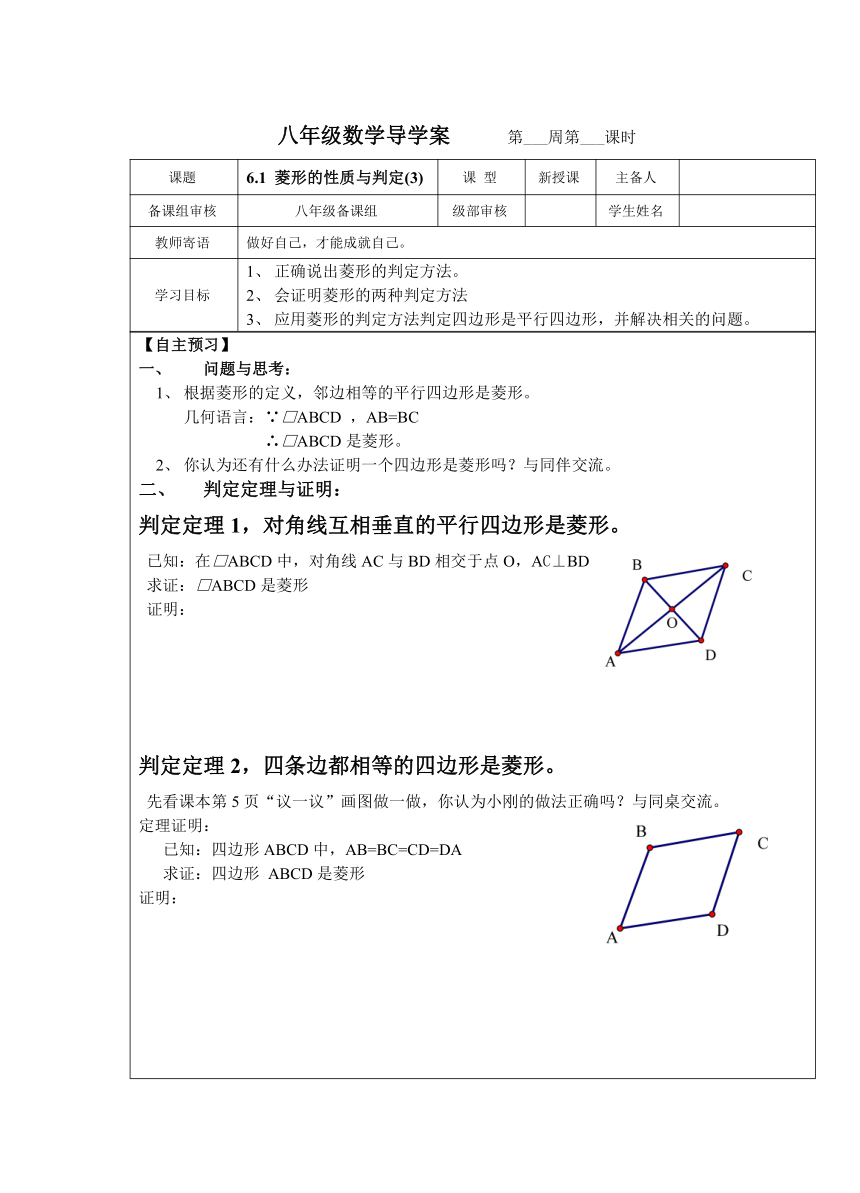
【自主预习】问题与思考:根据菱形的定义,邻边相等的平行四边形是菱形。几何语言:∵□ABCD ,AB=BC ∴□ABCD是菱形。你认为还有什么办法证明一个四边形是菱形吗?与同伴交流。判定定理与证明:判定定理1,对角线互相垂直的平行四边形是菱形。 已知:在□ABCD中,对角线AC与BD相交于点O,AC⊥BD 求证:□ABCD是菱形 证明:判定定理2,四条边都相等的四边形是菱形。 先看课本第5页“议一议”画图做一做,你认为小刚的做法正确吗?与同桌交流。定理证明: 已知:四边形ABCD中,AB=BC=CD=DA 求证:四边形 ABCD是菱形证明:【合作探究】例2.平行四边形ABCD中,对角线AC与BD交于点O,AB= ,OA=2,OB=1,求证ABCD是菱形 .【当堂反馈】:1.判断题(对的打“∨”,错的打“×):(1)有一组邻边相等的四边形是菱形; ( )(2)对角线互相垂直的四边形是菱形; ( )(3)对角线互相垂直平分的四边形是菱形.( )2、选择题(1)下列条件中,能判定四边形是菱形的是( )A、对角线垂直 B、两对角线相等C、两对角线互相平分 D、两对角线互相垂直平分(2)下列条件中不能判定四边形ABCD是菱形的是( ) A. □ABCD中,AB=BC B. □ABCD中,AC⊥BD C. □ABCD中,AC=BD D.□ABCD中,AC平分∠BAD3、解答题:已知:如图,在□ABCD中,对角线AC的垂直平分线分别于AD、AC、BC相交于点E、O、F。求证:四边形AFCE是菱形4、AD是⊿ABC的角平分线,DE∥BC,DF∥AB。 求证:四边形AEDF是菱形【课堂小结】
自我评价专栏 自主学习: 合作与交流: 书写: 综合:
课题 6.1 菱形的性质与判定(3) 课 型 新授课 主备人
备课组审核 八年级备课组 级部审核 学生姓名
教师寄语 做好自己,才能成就自己。
学习目标 正确说出菱形的判定方法。会证明菱形的两种判定方法应用菱形的判定方法判定四边形是平行四边形,并解决相关的问题。
【自主预习】问题与思考:根据菱形的定义,邻边相等的平行四边形是菱形。几何语言:∵□ABCD ,AB=BC ∴□ABCD是菱形。你认为还有什么办法证明一个四边形是菱形吗?与同伴交流。判定定理与证明:判定定理1,对角线互相垂直的平行四边形是菱形。 已知:在□ABCD中,对角线AC与BD相交于点O,AC⊥BD 求证:□ABCD是菱形 证明:判定定理2,四条边都相等的四边形是菱形。 先看课本第5页“议一议”画图做一做,你认为小刚的做法正确吗?与同桌交流。定理证明: 已知:四边形ABCD中,AB=BC=CD=DA 求证:四边形 ABCD是菱形证明:【合作探究】例2.平行四边形ABCD中,对角线AC与BD交于点O,AB= ,OA=2,OB=1,求证ABCD是菱形 .【当堂反馈】:1.判断题(对的打“∨”,错的打“×):(1)有一组邻边相等的四边形是菱形; ( )(2)对角线互相垂直的四边形是菱形; ( )(3)对角线互相垂直平分的四边形是菱形.( )2、选择题(1)下列条件中,能判定四边形是菱形的是( )A、对角线垂直 B、两对角线相等C、两对角线互相平分 D、两对角线互相垂直平分(2)下列条件中不能判定四边形ABCD是菱形的是( ) A. □ABCD中,AB=BC B. □ABCD中,AC⊥BD C. □ABCD中,AC=BD D.□ABCD中,AC平分∠BAD3、解答题:已知:如图,在□ABCD中,对角线AC的垂直平分线分别于AD、AC、BC相交于点E、O、F。求证:四边形AFCE是菱形4、AD是⊿ABC的角平分线,DE∥BC,DF∥AB。 求证:四边形AEDF是菱形【课堂小结】
自我评价专栏 自主学习: 合作与交流: 书写: 综合:
