北师大版数学七年级下册 4.3.2探索三角形全等的条件-课件(25张ppt)
文档属性
| 名称 | 北师大版数学七年级下册 4.3.2探索三角形全等的条件-课件(25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 323.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 21:12:41 | ||
图片预览






文档简介
(共25张PPT)
4.3.2探索三角形全等的条件(2)
(ASA和AAS)
复习
已知AB=DC,AC=DB, 那么∠A与∠D相等吗?为什么?
AB=DC( )
AC=DB( )
BC=CB( )
∴△ABC≌△DCB( )
∴∠A=∠D
已知
已知
公共边
SSS
(全等三角形的对应角相等)
解:在△ABC和△DCB中
A
B
C
D
复习
我们知道:如果给出一个三角形三条边的长度,那么因此得到的三角形都是全等.如果已知一个三角形的两角及一边,那么有几种可能的情况呢
每种情况下得到的三角形都全等吗
1、角.边.角;
2、角.角.边
做一做:课本100页
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°它们所夹的边为8cm,你能画出这个三角形吗
你画的三角形与同伴画的一定全等吗
60°
80°
做一做:课本100页
A
B
C
D
E
F
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
做一做:课本100页
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA)
几何语言:
A
B
C
D
E
F
做一做:课本100页
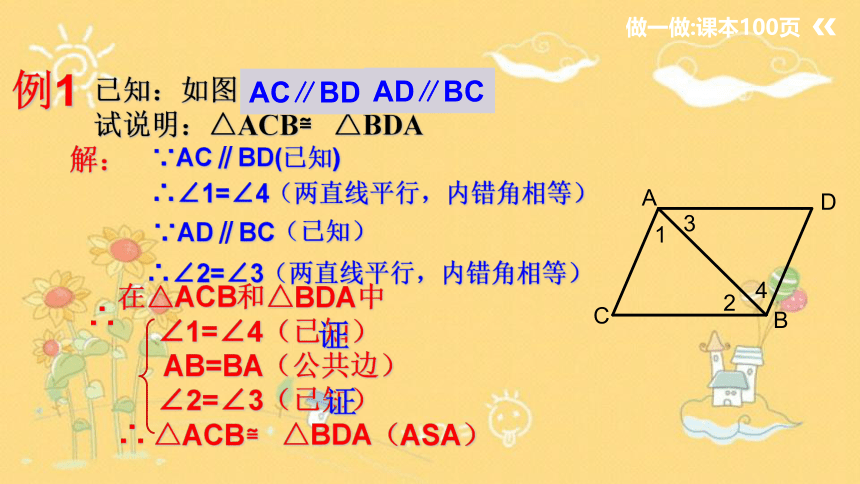
例1
已知:如图 ∠1=∠4, ∠2=∠3
试说明:△ACB≌ △BDA
解:
在△ACB和△BDA中
∠1=∠4(已知)
AB=BA(公共边)
∠2=∠3(已知)
∴ △ACB≌ △BDA(ASA)
∴∠2=∠3(两直线平行,内错角相等)
∵AC∥BD(已知)
∴∠1=∠4(两直线平行,内错角相等)
∵AD∥BC(已知)
∴
证
证
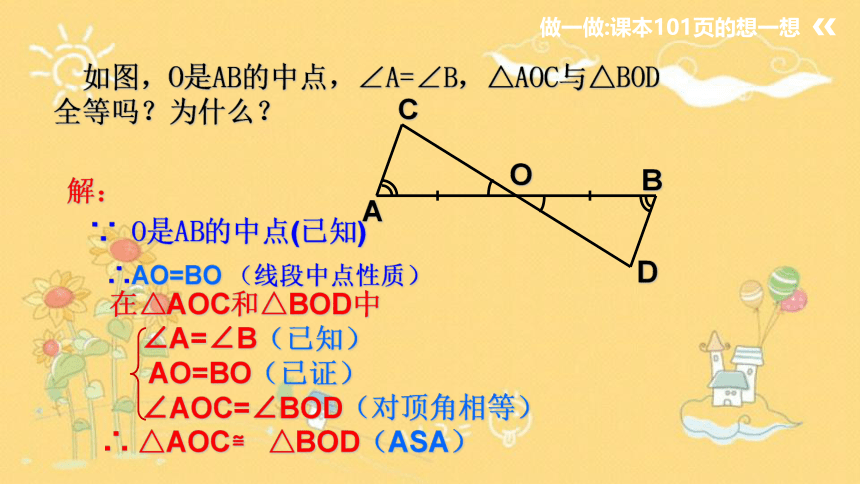
做一做:课本101页的想一想
如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
A
B
C
D
O
在△AOC和△BOD中
∠A=∠B(已知)
AO=BO(已证)
∠AOC=∠BOD(对顶角相等)
∴ △AOC≌ △BOD(ASA)
解:
∵ O是AB的中点(已知)
∴AO=BO (线段中点性质)
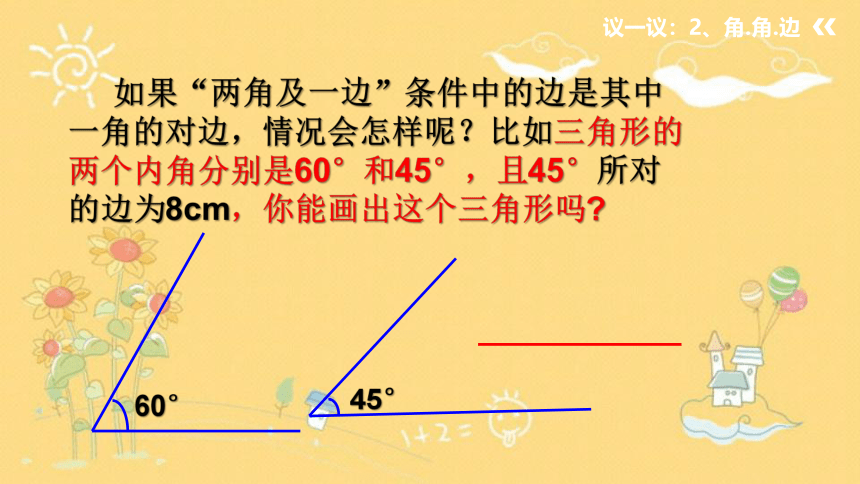
议一议:2、角.角.边
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?比如三角形的两个内角分别是60°和45°,且45°所对的边为8cm,你能画出这个三角形吗
60°
45°
议一议:2、角.角.边
A
B
C
D
E
F
两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”
议一议:2、角.角.边
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS)
几何语言:
A
B
C
D
E
F
议一议:2、角.角.边
例2、如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的角平分线,那么AB=AC吗?为什么?
1
2
A
B
C
D
1
2
A
B
C
D
证明:∵ AD是∠BAC的角平分线
∴ ∠ 1=∠2 (角平分线定义)
在△ABD与△ACD中
∠1= ∠2 (已证)
∠B=∠C (已知)
AD=AD (公共边)
∴ △ABD≌△ACD(AAS)
∴ AB=AC(全等三角形对应边相等)
练习
1,如图,∠B=∠C ,AD平分∠BAC,
试说明:△ABD≌△ACD;若BD=3cm,则CD有多长?
解:∵AD平分∠BAC(已知)
∴∠1=∠2(角平分线的定义)
∴在△ABD和△ACD中
∠1=∠2(已证)
∠B=∠C(已知)
AD=AD(公共边)
∴△ABD≌△ACD(AAS)
∴CD=BD=3㎝(全等三角形的对应边相等)
1
2
3cm
练习
2,图中的两个三角形全等吗 请说明理由.
A
B
C
D
(已知)
(已知)
(公共边)
变式练习
1、完成下列推理过程:
在△ABC和△DCB中,
∠ABC=∠DCB
∵ BC=CB
∴△ABC≌△DCB( )
ASA
A
B
C
D
O
1
2
3
4
( )
公共边
∠2=∠1
AAS
∠3=∠4
∠2=∠1
CB=BC
变式练习
A
B
C
D
E
1
2
2.如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
解: △ABC和△ADE全等,理由如下:
∵∠1=∠2(已知)
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ABC和△ADC 中
∴ △ABC≌△ADE
(AAS)
思考题
1,如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?
A
B
C
D
1
2
3
4
∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2
∠3=∠4 (两直线平行,内错角相等)
∴在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA)
∴ AB=CD BC=AD(全等三角形对应边相等)
解:相等,理由如下
连接AC
思考题
2.如图,∠C=∠D,DE=EC,
求证:(1)△DEB≌△CEA;(2)OA=OB.
思考题
思考题
3. 如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试说明:(1)△BDA≌△AEC;
解:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
思考题
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
解:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
课堂小结
本节课我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另两个定理 ,它们分别是:
1)两角和它们的夹边对应相等的两个三角形全等(ASA);
2)两角和其中一角的对边对应相等的两个三角形全等(AAS)。
再加上前面学的(SSS),证明两个三角形全等共有三个定理,我们要学会根据题目给出的条件选用合适的定理来证明两个三角形全等。
课堂小结
(1)如图①,已知:△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,
求证:DE=BD+CE;
课堂小结
(2)拓展:如图②,将(1)中的条件改为:△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问:结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
课堂小结
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,
求:△ABD与△CEF的面积之和.
4.3.2探索三角形全等的条件(2)
(ASA和AAS)
复习
已知AB=DC,AC=DB, 那么∠A与∠D相等吗?为什么?
AB=DC( )
AC=DB( )
BC=CB( )
∴△ABC≌△DCB( )
∴∠A=∠D
已知
已知
公共边
SSS
(全等三角形的对应角相等)
解:在△ABC和△DCB中
A
B
C
D
复习
我们知道:如果给出一个三角形三条边的长度,那么因此得到的三角形都是全等.如果已知一个三角形的两角及一边,那么有几种可能的情况呢
每种情况下得到的三角形都全等吗
1、角.边.角;
2、角.角.边
做一做:课本100页
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°它们所夹的边为8cm,你能画出这个三角形吗
你画的三角形与同伴画的一定全等吗
60°
80°
做一做:课本100页
A
B
C
D
E
F
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
做一做:课本100页
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA)
几何语言:
A
B
C
D
E
F
做一做:课本100页
例1
已知:如图 ∠1=∠4, ∠2=∠3
试说明:△ACB≌ △BDA
解:
在△ACB和△BDA中
∠1=∠4(已知)
AB=BA(公共边)
∠2=∠3(已知)
∴ △ACB≌ △BDA(ASA)
∴∠2=∠3(两直线平行,内错角相等)
∵AC∥BD(已知)
∴∠1=∠4(两直线平行,内错角相等)
∵AD∥BC(已知)
∴
证
证
做一做:课本101页的想一想
如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
A
B
C
D
O
在△AOC和△BOD中
∠A=∠B(已知)
AO=BO(已证)
∠AOC=∠BOD(对顶角相等)
∴ △AOC≌ △BOD(ASA)
解:
∵ O是AB的中点(已知)
∴AO=BO (线段中点性质)
议一议:2、角.角.边
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?比如三角形的两个内角分别是60°和45°,且45°所对的边为8cm,你能画出这个三角形吗
60°
45°
议一议:2、角.角.边
A
B
C
D
E
F
两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”
议一议:2、角.角.边
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS)
几何语言:
A
B
C
D
E
F
议一议:2、角.角.边
例2、如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的角平分线,那么AB=AC吗?为什么?
1
2
A
B
C
D
1
2
A
B
C
D
证明:∵ AD是∠BAC的角平分线
∴ ∠ 1=∠2 (角平分线定义)
在△ABD与△ACD中
∠1= ∠2 (已证)
∠B=∠C (已知)
AD=AD (公共边)
∴ △ABD≌△ACD(AAS)
∴ AB=AC(全等三角形对应边相等)
练习
1,如图,∠B=∠C ,AD平分∠BAC,
试说明:△ABD≌△ACD;若BD=3cm,则CD有多长?
解:∵AD平分∠BAC(已知)
∴∠1=∠2(角平分线的定义)
∴在△ABD和△ACD中
∠1=∠2(已证)
∠B=∠C(已知)
AD=AD(公共边)
∴△ABD≌△ACD(AAS)
∴CD=BD=3㎝(全等三角形的对应边相等)
1
2
3cm
练习
2,图中的两个三角形全等吗 请说明理由.
A
B
C
D
(已知)
(已知)
(公共边)
变式练习
1、完成下列推理过程:
在△ABC和△DCB中,
∠ABC=∠DCB
∵ BC=CB
∴△ABC≌△DCB( )
ASA
A
B
C
D
O
1
2
3
4
( )
公共边
∠2=∠1
AAS
∠3=∠4
∠2=∠1
CB=BC
变式练习
A
B
C
D
E
1
2
2.如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
解: △ABC和△ADE全等,理由如下:
∵∠1=∠2(已知)
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ABC和△ADC 中
∴ △ABC≌△ADE
(AAS)
思考题
1,如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?
A
B
C
D
1
2
3
4
∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2
∠3=∠4 (两直线平行,内错角相等)
∴在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA)
∴ AB=CD BC=AD(全等三角形对应边相等)
解:相等,理由如下
连接AC
思考题
2.如图,∠C=∠D,DE=EC,
求证:(1)△DEB≌△CEA;(2)OA=OB.
思考题
思考题
3. 如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.试说明:(1)△BDA≌△AEC;
解:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
思考题
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
解:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
课堂小结
本节课我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另两个定理 ,它们分别是:
1)两角和它们的夹边对应相等的两个三角形全等(ASA);
2)两角和其中一角的对边对应相等的两个三角形全等(AAS)。
再加上前面学的(SSS),证明两个三角形全等共有三个定理,我们要学会根据题目给出的条件选用合适的定理来证明两个三角形全等。
课堂小结
(1)如图①,已知:△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,
求证:DE=BD+CE;
课堂小结
(2)拓展:如图②,将(1)中的条件改为:△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问:结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
课堂小结
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,
求:△ABD与△CEF的面积之和.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
