6.4.1平面几何中的向量方法6.4.2向量在物理中的应用举例 课件(共28张PPT)
文档属性
| 名称 | 6.4.1平面几何中的向量方法6.4.2向量在物理中的应用举例 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 11:28:34 | ||
图片预览





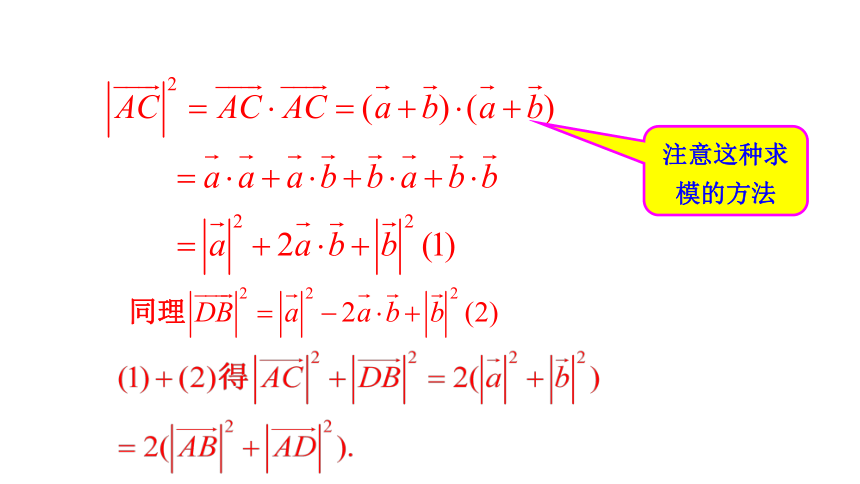


文档简介
(共28张PPT)
6.4平面向量的应用
6.4.1平面几何中的向量方法
6.4.2向量在物理中的应用举例
由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何图形的许多性质,如平移、全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来,因此,可用向量方法解决平面几何中的一些问题,下面我们通过几个具体实例,说明向量方法在平面几何中的运用.
向量概念源于物理中的矢量,物理中的力、位移、速度等都是向量,功是向量的数量积,从而使得向量与物理学建立了有机的内在联系,物理中具有矢量意义的问题也可以转化为向量问题来解决.因此,在实际问题中,如何运用向量方法分析和解决物理问题,又是一个值得探讨的课题.
通过向量在物理中的应用进一步培养学生的数学建模,数学运算能力
1.能利用向量的知识解决几何中的长度、角度、垂直等问题.
2.明确平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示. (重点、难点)
3.通过力的合成与分解模型、速度的合成与分解模型,掌握利用向量方法研究物理中相关问题的步骤.
4.掌握向量在物理中应用的基本题型,进一步加深对所学向量的概念和向量运算的认识.(难点)
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
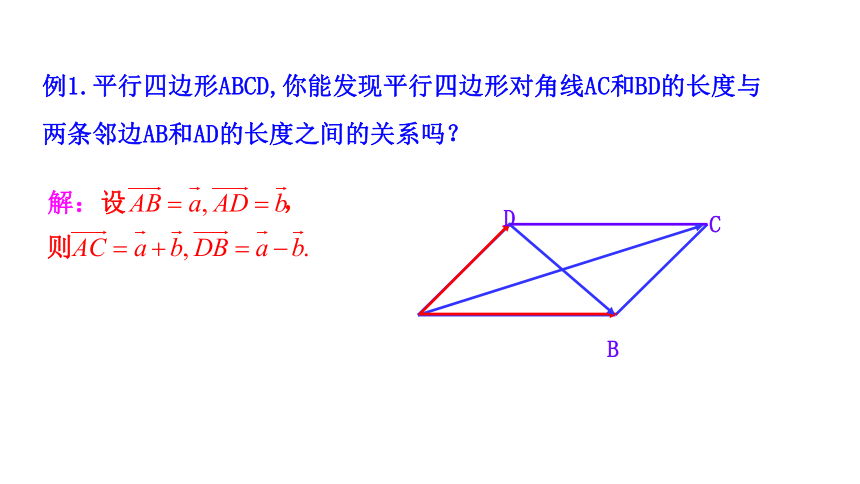
例1.平行四边形ABCD,你能发现平行四边形对角线AC和BD的长度与两条邻边AB和AD的长度之间的关系吗?
B
C
D
注意这种求模的方法
平行四边形两条对角线长的平方和等于两条邻边长的平方和的两倍.
如果不用向量方法,你能证明上述结论吗?
【方法规律】
用向量方法解决平面几何问题的“三步法”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题.
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题.
(3)把运算结果“翻译”成几何元素.
几何问题向量化
向量运算关系化
向量关系几何化
【变式练习】
利用向量解决力(速度、位移)的合成与分解
例2.在日常生活中,我们有这样的经验:两个人共提一个旅行包,两个拉力夹角越大越费劲;在单杠上做引体向上运动,两臂的夹角越小越省力。你能从数学的角度解释这种现象吗?
思考1:若两只手臂的拉力为 物体的重力为
那么 三个力之间具有什么关系?
思考2:假设两只手臂的拉力大小相等,夹角为θ,
那么| |,| |,θ之间的关系如何?
θ
提示:
思考3:上述结论表明,若重力 一定,则拉力的大小是关于夹角θ的函数.在物理学背景下,这个函数的定义域是什么?单调性如何?
提示:
增函数
思考4: | |有最小值吗?| |与| |可能相等吗?为什么?
提示:
用向量解力学问题
对物体进行受力分析
画出受力分析图
转化为向量问题
10N
A
C
B
D
A
C
B
D
A
B
答:行驶航程最短时,所用时间是3.1 min.
【变式练面几何中的向量方法
向量在物理中的应用举例
1.向量方法解决平面几何问题“三步曲”.
2. 用向量法解决物理问题.
核心知识
核心素养
1.数学抽象:平面几何图形的有关问题,用向量
的线性运算及数量积表示.
2.数学运算:向量的线性运算及数量积表示.
3.数学建模:数形结合,将物理问题向量化.
C
【解题关键】代入法求轨迹方程
设出P(x,y)和R(x0,y0)的坐标,用 P的坐标表示R点的坐标,之后代入已知直线方程化简即得。
黎明的曙光对暗夜是彻底的决裂,对彩霞是伟大的奠基。
停止前进的脚步,江河就会沦为一潭死水。
6.4平面向量的应用
6.4.1平面几何中的向量方法
6.4.2向量在物理中的应用举例
由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何图形的许多性质,如平移、全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来,因此,可用向量方法解决平面几何中的一些问题,下面我们通过几个具体实例,说明向量方法在平面几何中的运用.
向量概念源于物理中的矢量,物理中的力、位移、速度等都是向量,功是向量的数量积,从而使得向量与物理学建立了有机的内在联系,物理中具有矢量意义的问题也可以转化为向量问题来解决.因此,在实际问题中,如何运用向量方法分析和解决物理问题,又是一个值得探讨的课题.
通过向量在物理中的应用进一步培养学生的数学建模,数学运算能力
1.能利用向量的知识解决几何中的长度、角度、垂直等问题.
2.明确平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示. (重点、难点)
3.通过力的合成与分解模型、速度的合成与分解模型,掌握利用向量方法研究物理中相关问题的步骤.
4.掌握向量在物理中应用的基本题型,进一步加深对所学向量的概念和向量运算的认识.(难点)
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
例1.平行四边形ABCD,你能发现平行四边形对角线AC和BD的长度与两条邻边AB和AD的长度之间的关系吗?
B
C
D
注意这种求模的方法
平行四边形两条对角线长的平方和等于两条邻边长的平方和的两倍.
如果不用向量方法,你能证明上述结论吗?
【方法规律】
用向量方法解决平面几何问题的“三步法”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题.
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题.
(3)把运算结果“翻译”成几何元素.
几何问题向量化
向量运算关系化
向量关系几何化
【变式练习】
利用向量解决力(速度、位移)的合成与分解
例2.在日常生活中,我们有这样的经验:两个人共提一个旅行包,两个拉力夹角越大越费劲;在单杠上做引体向上运动,两臂的夹角越小越省力。你能从数学的角度解释这种现象吗?
思考1:若两只手臂的拉力为 物体的重力为
那么 三个力之间具有什么关系?
思考2:假设两只手臂的拉力大小相等,夹角为θ,
那么| |,| |,θ之间的关系如何?
θ
提示:
思考3:上述结论表明,若重力 一定,则拉力的大小是关于夹角θ的函数.在物理学背景下,这个函数的定义域是什么?单调性如何?
提示:
增函数
思考4: | |有最小值吗?| |与| |可能相等吗?为什么?
提示:
用向量解力学问题
对物体进行受力分析
画出受力分析图
转化为向量问题
10N
A
C
B
D
A
C
B
D
A
B
答:行驶航程最短时,所用时间是3.1 min.
【变式练面几何中的向量方法
向量在物理中的应用举例
1.向量方法解决平面几何问题“三步曲”.
2. 用向量法解决物理问题.
核心知识
核心素养
1.数学抽象:平面几何图形的有关问题,用向量
的线性运算及数量积表示.
2.数学运算:向量的线性运算及数量积表示.
3.数学建模:数形结合,将物理问题向量化.
C
【解题关键】代入法求轨迹方程
设出P(x,y)和R(x0,y0)的坐标,用 P的坐标表示R点的坐标,之后代入已知直线方程化简即得。
黎明的曙光对暗夜是彻底的决裂,对彩霞是伟大的奠基。
停止前进的脚步,江河就会沦为一潭死水。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
