9.2.1总体取值规律的估计9.2.2总体百分位数的估计 课件(共36张PPT)
文档属性
| 名称 | 9.2.1总体取值规律的估计9.2.2总体百分位数的估计 课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 11:31:09 | ||
图片预览










文档简介
(共36张PPT)
9.2 用样本估计总体
9.2.1总体取值规律的估计
9.2.2总体百分位数的估计
一个统计小故事的启示
1.结合实例,能用样本估计总体的取值规律.
2.会列频率分布表,画频率分布直方图.
3.能根据频率分布表和频率分布直方图观测数据的分布规律.
4.理解百分位数的统计含义,会求样本数据的第p百分位数.
1.直观想象:频率分布直方图的绘制与应用;
2.数学抽象:百分位数的统计含义;
3.数学运算:频率分布直方图中的相关计算问题,求第p百分位数.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
微课1 频率分布直方图
思考1我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.
如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.4 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
如果将这组数据从小到大排序,容易发现,这组数据的最小值是1.3t,最大值是28.0t,其他在1.3t至28.0t之间.
如果想得到更多的信息,可以如何做
思考:如何画频率分布直方图
1.求极差:
极差为一组数据中最大值与最小值的差.
样本观测数据的最小值是1.3t,最大值是28.0t,
极差为28.0-1.3=26.7
这说明样本观测数据的变化范围是26.7t.
2.决定组距与组数:
数据分组的组数与数据的个数有关,一般数据的个数越多,所分组数也越多,
当样本容量不超过100时,常分成5~12组.为方便起见,一般取等长组距,并且组距应力求“取整”分组时可以先确定组距,也可以先确定组数,如果我们取所有组距为3,则 即可将数据分为9组
3.将数据分组:
由于组距为3,9个组距的长度超过极差,我们可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值,例如,可以取区间为[1.2,28.2],按如下方式把样本观测数据以组距3分为9组:[1.2,4.2),[4.2,7.2),...,[25.2,28.2].
4.列频率分布表
计算各小组的频率,例如第一小组的频率
作出频率分布表
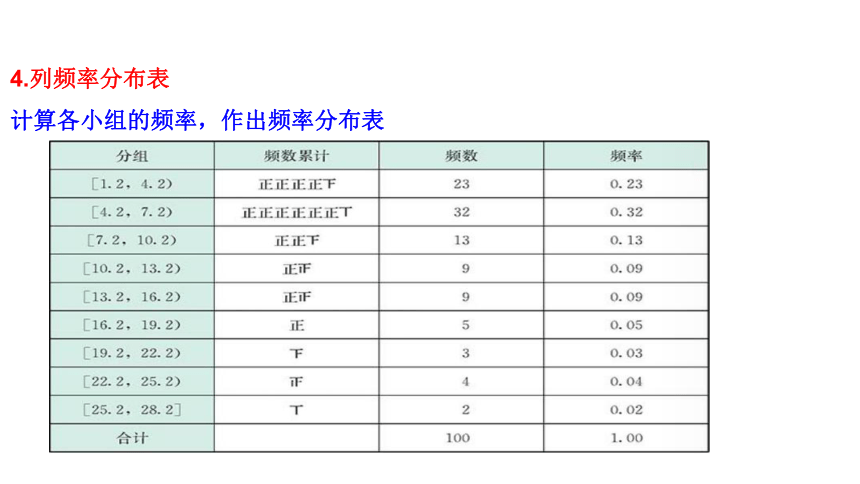
4.列频率分布表
计算各小组的频率,作出频率分布表
月均用水量/t
0.02
0.04
0.06
0.08
0.10
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.12
频率/组距
小长方形的面积=
5.画频率分布直方图
根据频率分布表画出如图所示的频率分布直方图
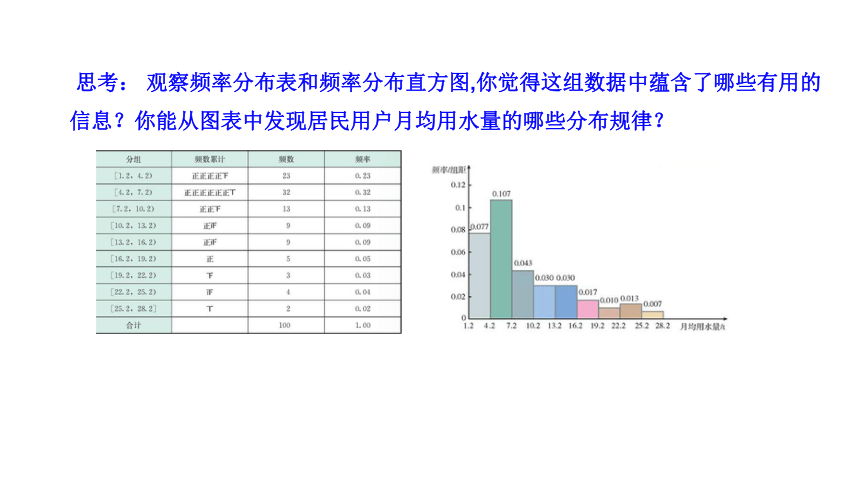
思考: 观察频率分布表和频率分布直方图,你觉得这组数据中蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?
(2)从频率分布直方图能直观的表明数据分布的形状和总体趋势.从上图容易看出,居民用户月均用水量的样本观测数据的分布是不对称的,图形的左边高、右边低,右边有一个较长的“尾巴”,这表明大部分居民用户的月均用水量集中在一个较低值区域,尤其在区间[1.2,7.2)最为集中,少数居民用户的月均用水量偏多,而且随着月均用水量的增加,居民用户数呈现降低趋势.
(1)从频率分布表中可以清楚地看出,样本观测数据落在各个小组的比例大小,例如,月均用水量在区间[4.2,7.2)内的居民用户最多,在区间[1.2,4.2)内的次之,而月均用水量超过16.2的各区间内数据所占比例较小,等等.
思考:分别以3和27为组数,对数据进行等距分组,画出100户居民用户月均用水量的频率分市直方图.观察图形,你发现不同的组数对于直方图呈现数据分市规律有什么影响
例1 某地区为了了解知识分子的年龄结构,
随机抽样50名,其年龄分别如下:
42,38,29,36,41,43,54,43,34,44,
40,59,39,42,44,50,37,44,45,29,
48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,67,
53,49,65,47,54,63,57,43,46,58.
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计年龄在32~52岁的知识分子所占的比例约是多少.
(1)极差为67-28=39,
取组距为5,分为8组.
分 组 频数 频率
[27,32) 3 0.06
[32,37) 3 0.06
[37,42) 8 0.16
[42,47) 16 0.32
[47,52) 8 0.16
[52,57) 5 0.10
[57,62) 4 0.08
[62,67] 4 0.08
合 计 50 1.00
样本频率分布表:
(2)样本频率分布直方图:
年龄
0.06
0.05
0.04
0.03
0.02
0.01
27 32 37 42 47 52 57 62 67
频率
组距
O
(3)因为0.06+0.16+0.32+0.16=0.7,
故年龄在32~52岁的知识分子约占70%.
【变式练习】
频率分布直方图如下:
思考: 根据市政府的要求确定居民用户月均用水量标准,就是要寻找一个数a,使全市居民用户月均用水量中不超过a的占80%,大于a的占20%. 你能给市政府提出确定居民用户月均用水量标准的建议吗?
把100个样本数据按从小到大排序,得到第80个和第81个数据分别为13.6和13.8.可以发现,区间(13.6,13.8)内的任意一个数,都能把样本数据分成符合要求的两部分.
一般地,我们取这两个数的平均数(13.6+13.8)÷2=13.7,
并称此数为这组数据的第80百分位数或80%分位数.
定义:
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
第p百分位数的定义
思考:计算一组n个数据的第p百分位数的步骤
可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为
第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)
项数据的平均数.
163.0 164.0 161.0 157.0 162.0 165.0 158.0 155.0 164.0 162.5 154.0 154.0 164.0 149.0 159.0 161.0 170.0 171.0 155.0 148.0 172.0 162.5 158.0 155.5 157.0 163.0 172.0
例2.根据下面女生的身高的样本数据,估计树人中学高一年级女生的第25,50,75百分位数.
解:把27名女生的样本数据按从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0 158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0 163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
由25%×27=6.75, 50%×27=13.5, 75%×27=20.25,
可知样本数据的第25,50,75百分位数为第7, 14,21项数据,分别为155.5,161,164.据此可以估计树人中学高一年级女生的第25,50,75百分位数分别约为155.5,161和164.
例3.根据下表或下图,估计月均用水量的样本数据的80%和95%分位数.
分析:统计表或统计图,与原始数据相比,它们损失了一些信息,例如由上表中可以知道在[16.2,19.2)内有5个数据,但不知道这5个数据具体是多少.此时,我们通常把它们看成均匀地分布在此区间上.
解:由表可知,月均用水量在13.2t以下的居民用户所占比例为23%+32%+13%+9%=77%.
在16.2t以下的居民用户所占的比例为77%+9%=86%.
因此,80%分位数一定位于[13.2,16.2)内.
由13.2+3× =14.2, 可以估计月均用水量的样本
数据的80%分位数约为14.2.
类似地,由22.2+3× =22.95,
可以估计月均用水量的样本数据的95%分位数约为22.95.
右表为12名毕业生的起始月薪
根据表中所给的数据计算第85百分位数.
:
毕业生 起始月薪 毕业生 起始月薪
1 2 850 7 2 890
2 2 950 8 3 130
3 3 050 9 2 940
4 2 880 10 3 325
5 2 755 11 2 920
6 2 710 12 2 880
解:计算i=12×85%=10.2,
所以所给数据的第85百分位数是从小到大的第11个数据3130
【变式练习】
总体取值规律的估计
总体百分位数的估计
绘制频率分布直方图的注意事项
(1)计算极差当数据很多时,可选一个数当参照.
(2)数据越多,分组越多。
(3)将数据分组决定分点时,一般使分点比数据多一位小数,并且把第一组的起点稍微减小一点。
(4)画频率分布直方图时,纵坐标表示频率与组距的比值,.
频率分布表
频率分布直方图
百分位数
核心知识
方法总结
易错提醒
核心素养
直观想象:在绘制频率分布直方图时体现的是直观想象的核心素养
第p百分位数
四分位数
其他统计图
扇形图
折线图
条形图
计算百分位数的步骤::
将原始数据排列→计算i=n×p%→若i不是整数,而大于i的比邻整数为j,则取与i相邻的第j 项数据;若i是整数,则取第i项与第(i+1)项数据的平均数.
2.下列一组数据的第25百分位数是( )
2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6
A.3.2 B.3.0 C.4.4 D.2.5
解 把该组数据按照由小到大排列,可得:
2.1,3.0,3.2,3.4,3.8,4.0,4.2,4.4,5.3,5.6,
由i=10×25%=2.5,
不是整数,则第3个数据3.2,是第25百分位数.
A
C
0.03
0.05
0.07
体重(kg)
频率/组距
54.5
58.5
62.5
66.5
70.5
74.5
6. 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的第50百分位数和第75百分位数吗
解:由题意知分别落在各区间上的频数为
在[80,90)上有60×0.15=9,
在[90,100)上有60×0.25=15,
在[100,110)上有60×0.3=18,
在[110,120)上有60×0.2=12,
在[120,130]上有60×0.1=6.
从以上数据可知第50百分位数一定落在区间[100,110)上,
综上可知,第50百分位数和第75百分位数分别估计为103.3 cm,112.5 cm.
黎明的曙光对暗夜是彻底的决裂,对彩霞是伟大的奠基。
停止前进的脚步,江河就会沦为一潭死水。
9.2 用样本估计总体
9.2.1总体取值规律的估计
9.2.2总体百分位数的估计
一个统计小故事的启示
1.结合实例,能用样本估计总体的取值规律.
2.会列频率分布表,画频率分布直方图.
3.能根据频率分布表和频率分布直方图观测数据的分布规律.
4.理解百分位数的统计含义,会求样本数据的第p百分位数.
1.直观想象:频率分布直方图的绘制与应用;
2.数学抽象:百分位数的统计含义;
3.数学运算:频率分布直方图中的相关计算问题,求第p百分位数.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
微课1 频率分布直方图
思考1我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.
如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.4 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
如果将这组数据从小到大排序,容易发现,这组数据的最小值是1.3t,最大值是28.0t,其他在1.3t至28.0t之间.
如果想得到更多的信息,可以如何做
思考:如何画频率分布直方图
1.求极差:
极差为一组数据中最大值与最小值的差.
样本观测数据的最小值是1.3t,最大值是28.0t,
极差为28.0-1.3=26.7
这说明样本观测数据的变化范围是26.7t.
2.决定组距与组数:
数据分组的组数与数据的个数有关,一般数据的个数越多,所分组数也越多,
当样本容量不超过100时,常分成5~12组.为方便起见,一般取等长组距,并且组距应力求“取整”分组时可以先确定组距,也可以先确定组数,如果我们取所有组距为3,则 即可将数据分为9组
3.将数据分组:
由于组距为3,9个组距的长度超过极差,我们可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值,例如,可以取区间为[1.2,28.2],按如下方式把样本观测数据以组距3分为9组:[1.2,4.2),[4.2,7.2),...,[25.2,28.2].
4.列频率分布表
计算各小组的频率,例如第一小组的频率
作出频率分布表
4.列频率分布表
计算各小组的频率,作出频率分布表
月均用水量/t
0.02
0.04
0.06
0.08
0.10
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.12
频率/组距
小长方形的面积=
5.画频率分布直方图
根据频率分布表画出如图所示的频率分布直方图
思考: 观察频率分布表和频率分布直方图,你觉得这组数据中蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?
(2)从频率分布直方图能直观的表明数据分布的形状和总体趋势.从上图容易看出,居民用户月均用水量的样本观测数据的分布是不对称的,图形的左边高、右边低,右边有一个较长的“尾巴”,这表明大部分居民用户的月均用水量集中在一个较低值区域,尤其在区间[1.2,7.2)最为集中,少数居民用户的月均用水量偏多,而且随着月均用水量的增加,居民用户数呈现降低趋势.
(1)从频率分布表中可以清楚地看出,样本观测数据落在各个小组的比例大小,例如,月均用水量在区间[4.2,7.2)内的居民用户最多,在区间[1.2,4.2)内的次之,而月均用水量超过16.2的各区间内数据所占比例较小,等等.
思考:分别以3和27为组数,对数据进行等距分组,画出100户居民用户月均用水量的频率分市直方图.观察图形,你发现不同的组数对于直方图呈现数据分市规律有什么影响
例1 某地区为了了解知识分子的年龄结构,
随机抽样50名,其年龄分别如下:
42,38,29,36,41,43,54,43,34,44,
40,59,39,42,44,50,37,44,45,29,
48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,67,
53,49,65,47,54,63,57,43,46,58.
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计年龄在32~52岁的知识分子所占的比例约是多少.
(1)极差为67-28=39,
取组距为5,分为8组.
分 组 频数 频率
[27,32) 3 0.06
[32,37) 3 0.06
[37,42) 8 0.16
[42,47) 16 0.32
[47,52) 8 0.16
[52,57) 5 0.10
[57,62) 4 0.08
[62,67] 4 0.08
合 计 50 1.00
样本频率分布表:
(2)样本频率分布直方图:
年龄
0.06
0.05
0.04
0.03
0.02
0.01
27 32 37 42 47 52 57 62 67
频率
组距
O
(3)因为0.06+0.16+0.32+0.16=0.7,
故年龄在32~52岁的知识分子约占70%.
【变式练习】
频率分布直方图如下:
思考: 根据市政府的要求确定居民用户月均用水量标准,就是要寻找一个数a,使全市居民用户月均用水量中不超过a的占80%,大于a的占20%. 你能给市政府提出确定居民用户月均用水量标准的建议吗?
把100个样本数据按从小到大排序,得到第80个和第81个数据分别为13.6和13.8.可以发现,区间(13.6,13.8)内的任意一个数,都能把样本数据分成符合要求的两部分.
一般地,我们取这两个数的平均数(13.6+13.8)÷2=13.7,
并称此数为这组数据的第80百分位数或80%分位数.
定义:
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
第p百分位数的定义
思考:计算一组n个数据的第p百分位数的步骤
可以通过下面的步骤计算一组n个数据的第p百分位数:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为
第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)
项数据的平均数.
163.0 164.0 161.0 157.0 162.0 165.0 158.0 155.0 164.0 162.5 154.0 154.0 164.0 149.0 159.0 161.0 170.0 171.0 155.0 148.0 172.0 162.5 158.0 155.5 157.0 163.0 172.0
例2.根据下面女生的身高的样本数据,估计树人中学高一年级女生的第25,50,75百分位数.
解:把27名女生的样本数据按从小到大排序,可得
148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0 158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0 163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0
由25%×27=6.75, 50%×27=13.5, 75%×27=20.25,
可知样本数据的第25,50,75百分位数为第7, 14,21项数据,分别为155.5,161,164.据此可以估计树人中学高一年级女生的第25,50,75百分位数分别约为155.5,161和164.
例3.根据下表或下图,估计月均用水量的样本数据的80%和95%分位数.
分析:统计表或统计图,与原始数据相比,它们损失了一些信息,例如由上表中可以知道在[16.2,19.2)内有5个数据,但不知道这5个数据具体是多少.此时,我们通常把它们看成均匀地分布在此区间上.
解:由表可知,月均用水量在13.2t以下的居民用户所占比例为23%+32%+13%+9%=77%.
在16.2t以下的居民用户所占的比例为77%+9%=86%.
因此,80%分位数一定位于[13.2,16.2)内.
由13.2+3× =14.2, 可以估计月均用水量的样本
数据的80%分位数约为14.2.
类似地,由22.2+3× =22.95,
可以估计月均用水量的样本数据的95%分位数约为22.95.
右表为12名毕业生的起始月薪
根据表中所给的数据计算第85百分位数.
:
毕业生 起始月薪 毕业生 起始月薪
1 2 850 7 2 890
2 2 950 8 3 130
3 3 050 9 2 940
4 2 880 10 3 325
5 2 755 11 2 920
6 2 710 12 2 880
解:计算i=12×85%=10.2,
所以所给数据的第85百分位数是从小到大的第11个数据3130
【变式练习】
总体取值规律的估计
总体百分位数的估计
绘制频率分布直方图的注意事项
(1)计算极差当数据很多时,可选一个数当参照.
(2)数据越多,分组越多。
(3)将数据分组决定分点时,一般使分点比数据多一位小数,并且把第一组的起点稍微减小一点。
(4)画频率分布直方图时,纵坐标表示频率与组距的比值,.
频率分布表
频率分布直方图
百分位数
核心知识
方法总结
易错提醒
核心素养
直观想象:在绘制频率分布直方图时体现的是直观想象的核心素养
第p百分位数
四分位数
其他统计图
扇形图
折线图
条形图
计算百分位数的步骤::
将原始数据排列→计算i=n×p%→若i不是整数,而大于i的比邻整数为j,则取与i相邻的第j 项数据;若i是整数,则取第i项与第(i+1)项数据的平均数.
2.下列一组数据的第25百分位数是( )
2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6
A.3.2 B.3.0 C.4.4 D.2.5
解 把该组数据按照由小到大排列,可得:
2.1,3.0,3.2,3.4,3.8,4.0,4.2,4.4,5.3,5.6,
由i=10×25%=2.5,
不是整数,则第3个数据3.2,是第25百分位数.
A
C
0.03
0.05
0.07
体重(kg)
频率/组距
54.5
58.5
62.5
66.5
70.5
74.5
6. 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的第50百分位数和第75百分位数吗
解:由题意知分别落在各区间上的频数为
在[80,90)上有60×0.15=9,
在[90,100)上有60×0.25=15,
在[100,110)上有60×0.3=18,
在[110,120)上有60×0.2=12,
在[120,130]上有60×0.1=6.
从以上数据可知第50百分位数一定落在区间[100,110)上,
综上可知,第50百分位数和第75百分位数分别估计为103.3 cm,112.5 cm.
黎明的曙光对暗夜是彻底的决裂,对彩霞是伟大的奠基。
停止前进的脚步,江河就会沦为一潭死水。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
