10.3.1频率的稳定性 课件(共23张PPT)
文档属性
| 名称 | 10.3.1频率的稳定性 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 14:12:15 | ||
图片预览







文档简介
(共23张PPT)
10.3频率与概率
10.3.1频率的稳定性
在相同的条件下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数,称事件A出现的比例
fn(A)= 为事件A出现的频率. 显然,0≤ ≤1.
1. 了解频率与概率的关系.
2. 结合实例,会用频率估计概率.
1.数学抽象:频率的稳定性的理解.
2.数学运算:概率的应用.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
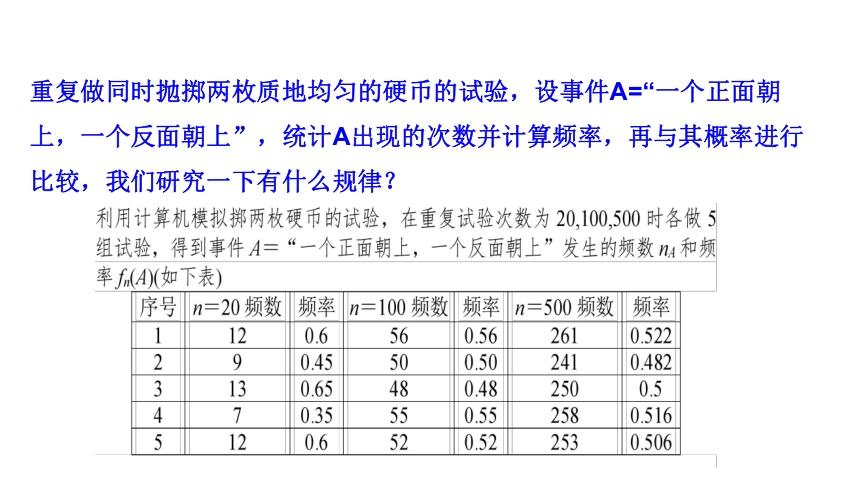
重复做同时抛掷两枚质地均匀的硬币的试验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,我们研究一下有什么规律?
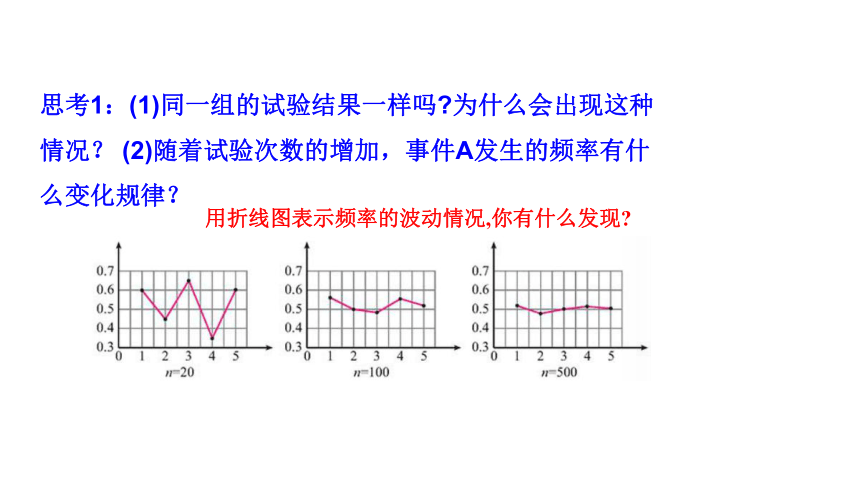
思考1:(1)同一组的试验结果一样吗 为什么会出现这种情况? (2)随着试验次数的增加,事件A发生的频率有什么变化规律?
用折线图表示频率的波动情况,你有什么发现
结论:
(1)试验次数n相同,频率fn(A)可能不同,这说明随机事件发生的频率具有随机性
(2)从整体来看,频率在概率0.5附近波动.当试验次数较少时,波动幅度较大;当试验次数较大时,波动幅度较小.但试验次数多的波动幅度并不全都比次数少的小,只是波动幅度小的可能性更大.
对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率,简称为A的概率。
思考2:频率与概率有什么区别和联系?
(1)频率本身是随机的,是一个变量,在试验前不能确定,做同样次数的重复试验得到的事件发生的频率会不同.
(2)概率是一个确定的数,是客观存在的,与每次的试验无关.
(3)频率是概率的近似值,随着试验次数的增加,频率会越来越稳定于概率附近.在实际问题中,通常事件发生的概率未知,常用频率作为它的估计值.
例1 新生婴儿性别比是每100名女婴对应的男婴数,通过抽样调查得知,我国2014年、2015年出生的婴儿性别比分别为115.88和113.51.
(1)分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);
(2)根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
分析:根据“性别比”的定义和抽样调查结果,可以计算男婴出生的频率;由频率的稳定性,可以估计男婴的出生率
解:(1)2014年男婴出生的频率为
2015年男婴出生的频率为
由此估计,我国2014年男婴出生率约为0.537,2015年男婴出生率约为0.532.
(2)由于调查新生儿人数的样本非常大,根据频率的稳定性,上述对男婴出生率的估计具有较高的可信度,因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
由统计定义求概率的一般步骤
(1)确定随机事件A的频数nA;
(2)由fn(A)= 计算频率fn(A) (n为试验的总次数);
(3)由频率fn(A)估计概率P(A).
概率可看成频率在理论上的稳定值,它从数量上反映了随机事件发生的可能性的大小,它是频率的科学抽象,当试验次数越来越多时频率向概率靠近,只要次数足够多,所得频率就近似地当作随机事件的概率.
例2.一个游戏包含两个随机事件A和B,规定事件A发生则甲获胜,事件
B发生则乙获胜,判断游戏是否公平的标准是事件A和B发生的概率是
否相等。在游戏过程中甲发现:玩了10次时,双方各胜5次;但玩到
1 000次时,自己才胜300次,而乙却胜了700次,据此,甲认为游戏不
公平,但乙认为游戏是公平的,你更支持谁的结论?为什么?
解:当游戏玩了10次时,甲、乙获胜的频率都为0.5;当游戏玩了1 000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.根据频率的稳定性,随着试验次数的增加,频率偏离概率很大的可能性会越来越小.相对10次游戏,1 000次游戏时的频率接近概率的可能性更大,因此我们更愿意相信1 000次时的频率离概率更近,而游戏玩到1 000次时,甲、乙获胜的频率分别是0.3和0.7,存在很大差距,所以有理由认为游戏是不公平的.因此,应该支持甲对游戏公平性的判断
思考:气象工作者有时用概率预报天气,如某气象台预报“明天的降水概率是90%.如果您明天要出门,最好携带雨具”,如果第二天没有下雨,我们或许会抱怨气象台预报得不准确,那么如何理解“降水概率是90%”?又该如何评价预报的结果是否准确呢?
提示:降水的概率是气象专家根据气象条件和经验,经分析推断得到的.对“降水的概率为90%”比较合理的解释是:大量观察发现,在类似的气象条件下,大约有90%的天数要下雨.
只有根据气象预报的长期记录,才能评价预报的准确性.如果在类似气象条件下预报要下雨的那些天(天数较多)里,大约有90%确实下雨了,那么应该认为预报是准确的;如果真实下雨的天数所占的比例与90%差别较大,那么就可以认为预报不太准确.
游戏公平性的判断:对游戏的双方来说,获胜的概率是否相等
频率是随机的数,概率是确定的数
数据分析:通过实例分析频率稳定性
数学抽象:通过实例了解频率与概率的区别与联系
核心知识
方法总结
易错提醒
核心素养
频率的稳定性
1.若经检验,某厂的产品合格率为98%,估算该厂8 000件产品中的次品件数为( )
A.7 840 B.160 C.16 D.784
B
2.一个袋中装有数量差别较大的白球和黑球,从中任取两球,取出的都是白球,估计袋中数量较少的球是____.
黑球
一次性购物数量 1至
4件 5至
8件 9至
12件 13至16件 17件及以上
顾客数(人) x 30 25 y 10
结算时间(分/人) 1 1.5 2 2.5 3
4.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100名顾客的相关数据,如下表所示:已知这100位顾客中一次性购物超过8件的顾客占55%.
(1)求x,y的值;
(2)求一位顾客一次购物的结算时间超过2分钟的概率.
环境不会改变,解决之道在于改变自己.
10.3频率与概率
10.3.1频率的稳定性
在相同的条件下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数,称事件A出现的比例
fn(A)= 为事件A出现的频率. 显然,0≤ ≤1.
1. 了解频率与概率的关系.
2. 结合实例,会用频率估计概率.
1.数学抽象:频率的稳定性的理解.
2.数学运算:概率的应用.
体会课堂探究的乐趣,
汲取新知识的营养,
让我们一起 吧!
进
走
课
堂
重复做同时抛掷两枚质地均匀的硬币的试验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,我们研究一下有什么规律?
思考1:(1)同一组的试验结果一样吗 为什么会出现这种情况? (2)随着试验次数的增加,事件A发生的频率有什么变化规律?
用折线图表示频率的波动情况,你有什么发现
结论:
(1)试验次数n相同,频率fn(A)可能不同,这说明随机事件发生的频率具有随机性
(2)从整体来看,频率在概率0.5附近波动.当试验次数较少时,波动幅度较大;当试验次数较大时,波动幅度较小.但试验次数多的波动幅度并不全都比次数少的小,只是波动幅度小的可能性更大.
对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率,简称为A的概率。
思考2:频率与概率有什么区别和联系?
(1)频率本身是随机的,是一个变量,在试验前不能确定,做同样次数的重复试验得到的事件发生的频率会不同.
(2)概率是一个确定的数,是客观存在的,与每次的试验无关.
(3)频率是概率的近似值,随着试验次数的增加,频率会越来越稳定于概率附近.在实际问题中,通常事件发生的概率未知,常用频率作为它的估计值.
例1 新生婴儿性别比是每100名女婴对应的男婴数,通过抽样调查得知,我国2014年、2015年出生的婴儿性别比分别为115.88和113.51.
(1)分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);
(2)根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
分析:根据“性别比”的定义和抽样调查结果,可以计算男婴出生的频率;由频率的稳定性,可以估计男婴的出生率
解:(1)2014年男婴出生的频率为
2015年男婴出生的频率为
由此估计,我国2014年男婴出生率约为0.537,2015年男婴出生率约为0.532.
(2)由于调查新生儿人数的样本非常大,根据频率的稳定性,上述对男婴出生率的估计具有较高的可信度,因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
由统计定义求概率的一般步骤
(1)确定随机事件A的频数nA;
(2)由fn(A)= 计算频率fn(A) (n为试验的总次数);
(3)由频率fn(A)估计概率P(A).
概率可看成频率在理论上的稳定值,它从数量上反映了随机事件发生的可能性的大小,它是频率的科学抽象,当试验次数越来越多时频率向概率靠近,只要次数足够多,所得频率就近似地当作随机事件的概率.
例2.一个游戏包含两个随机事件A和B,规定事件A发生则甲获胜,事件
B发生则乙获胜,判断游戏是否公平的标准是事件A和B发生的概率是
否相等。在游戏过程中甲发现:玩了10次时,双方各胜5次;但玩到
1 000次时,自己才胜300次,而乙却胜了700次,据此,甲认为游戏不
公平,但乙认为游戏是公平的,你更支持谁的结论?为什么?
解:当游戏玩了10次时,甲、乙获胜的频率都为0.5;当游戏玩了1 000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.根据频率的稳定性,随着试验次数的增加,频率偏离概率很大的可能性会越来越小.相对10次游戏,1 000次游戏时的频率接近概率的可能性更大,因此我们更愿意相信1 000次时的频率离概率更近,而游戏玩到1 000次时,甲、乙获胜的频率分别是0.3和0.7,存在很大差距,所以有理由认为游戏是不公平的.因此,应该支持甲对游戏公平性的判断
思考:气象工作者有时用概率预报天气,如某气象台预报“明天的降水概率是90%.如果您明天要出门,最好携带雨具”,如果第二天没有下雨,我们或许会抱怨气象台预报得不准确,那么如何理解“降水概率是90%”?又该如何评价预报的结果是否准确呢?
提示:降水的概率是气象专家根据气象条件和经验,经分析推断得到的.对“降水的概率为90%”比较合理的解释是:大量观察发现,在类似的气象条件下,大约有90%的天数要下雨.
只有根据气象预报的长期记录,才能评价预报的准确性.如果在类似气象条件下预报要下雨的那些天(天数较多)里,大约有90%确实下雨了,那么应该认为预报是准确的;如果真实下雨的天数所占的比例与90%差别较大,那么就可以认为预报不太准确.
游戏公平性的判断:对游戏的双方来说,获胜的概率是否相等
频率是随机的数,概率是确定的数
数据分析:通过实例分析频率稳定性
数学抽象:通过实例了解频率与概率的区别与联系
核心知识
方法总结
易错提醒
核心素养
频率的稳定性
1.若经检验,某厂的产品合格率为98%,估算该厂8 000件产品中的次品件数为( )
A.7 840 B.160 C.16 D.784
B
2.一个袋中装有数量差别较大的白球和黑球,从中任取两球,取出的都是白球,估计袋中数量较少的球是____.
黑球
一次性购物数量 1至
4件 5至
8件 9至
12件 13至16件 17件及以上
顾客数(人) x 30 25 y 10
结算时间(分/人) 1 1.5 2 2.5 3
4.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100名顾客的相关数据,如下表所示:已知这100位顾客中一次性购物超过8件的顾客占55%.
(1)求x,y的值;
(2)求一位顾客一次购物的结算时间超过2分钟的概率.
环境不会改变,解决之道在于改变自己.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
