10.1.1有限样本空间与随机事件 课件(共25张PPT)
文档属性
| 名称 | 10.1.1有限样本空间与随机事件 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 14:16:41 | ||
图片预览








文档简介
(共25张PPT)
第十章 概率
概率论的产生和发展
传说早在1654年,有一个赌徒梅累向当时的数学家帕斯卡提出一个使他苦恼了很久的问题:“两个赌徒约定谁先赢满5局,谁就获得全部赌金。赌了半天, A赢了4局, B赢了3局,时间很晚了,他们都不想再赌下去了。那么,这个钱应该怎么分才理?
这个问题让帕斯卡苦苦思索了三年,三年后也就是1657年,
荷兰著名的数学家惠更斯企图自己解决这一问题,结果写成了
《论赌博中的计算》一书,这就是概率论最早的一部著作。
1.了解随机试验、样本空间的概念.
2.通过实例,了解必然事件、不可能事件与随机事件的含义.
1.数学抽象:随机试验、样本空间、样本容量的概念.
2.数据分析:判断必然事件、不可能事件与随机事件.
3.数学运算:写出事件的样本空间.
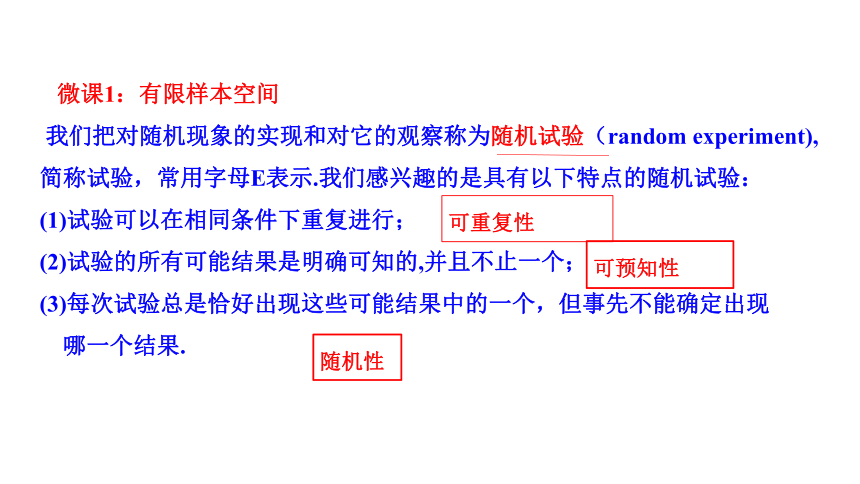
微课1:有限样本空间
我们把对随机现象的实现和对它的观察称为随机试验(random experiment),简称试验,常用字母E表示.我们感兴趣的是具有以下特点的随机试验:
(1)试验可以在相同条件下重复进行;
(2)试验的所有可能结果是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现
哪一个结果.
可重复性
可预知性
随机性
思考1:体育彩票摇奖时,将10个质地和大小完全相同、分别标号0,1,2,…,9的球放入摇奖器中,经过充分搅拌后摇出一个球,观察这个球的号码,这个随机试验共有多少个可能结果?如何表示这些结果?
共有10种可能结果.
所有可能结果可用集合表示为:{0,1,2,3,4,5,6,7,8,9}
样本点与样本空间
(1)样本点:随机试验E的每个可能的基本结果称为样本点;
(2)样本空间:全体样本点的集合称为试验E的样本空间.
一般地,用Ω表示样本空间,用ω表示样本点;
(3)有限样本空间:如果一个随机试验有n个可能结果ω1,ω2,…, ωn,
则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
解:因为落地时只有正面朝上和反面朝上两个可能结果,所以试
验的样本空间可以表示为Ω =(正面朝上,反面朝上),如果
用h表示“正面朝上”,t表示“反面朝上”,则样本空间
Ω ={h,t}.
典例解析
例1.抛掷一枚硬币,观察它落地时哪一面朝上,写出试验的样本空间。
例2 .抛掷一枚骰子(touzi),观察它落地时朝上的面的点数,写出试验的
样本空间.
解:用i表示朝上面的“点数为i”,
因为落地时朝上面的点数有1,2,3,4,5,6共6个可能的基本结果,
所以试验的样本空间可以表示为Ω ={1,2,3,4,5,6}.
解法一:掷两枚硬币,第一枚硬币可能的基本结果用x表示,
第二枚硬币可能的基本结果用y表示,
那么试验的样本点可用(x,y)表示.于是,试验的样本空间
Ω ={(正面,正面),(正面,反面),(反面,正面),(反面,反面)}
例3.抛掷两枚硬币,观察它们落地时朝上的面的情况,写出试验的样
本空间
解法二:如果我们用1表示硬币“正面朝上”,用0表示硬币“反面朝 上”,那么样本空间还可以简单表示为Ω={(1,1),(1,0),(0,1),(0,0)}.
如图所示,画树状图可以帮助我们理
解例3的解答过程.
类题通法
(1)如何确定试验的样本空间?
提示:要考虑周全,应想到试验的所有可能的结果,避免发生遗漏和出现多余或者重复的结果.
(2)写试验的样本空间要注意些什么?
提示:确定试验的样本空间就是写出试验的所有可能的结果,并写成Ω={ω1,ω2,…,ωn}的形式.
解:(1)Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),
(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}.
(2)样本点的总数为16.
(3)“x+y=5”包含以下4个样本点:(1,4),(2,3),(3,2),(1,4);
“x<3且y>1”包含以下6个样本点:(1,2),(1,3),(1,4),(2,2),(2,3),(2,4).
(4)“xy=4”包含以下3个样本点:(1,4),(2,2),(4,1);
“x=y”包含以下4个样本点:(1,1),(2,2),(3,3),(4,4).
微课2: 随机事件
思考: 在体育彩票摇号实验中,摇出“球的号码是奇数”是随机事件吗?摇出“球的号码为3的倍数”是否也是随机事件?如果用集合的形式来表示它们,那么这些集合与样本空间有什么关系?
显然,“球的号码为奇数”和“球的号码为3的倍数”都是随机事件.
我们用A表示随机事件“球的号码为奇数”,则A发生,当且仅当摇出的号码为1,3,5,7,9之一,即事件A发生等价于摇出的号码属于集合{1,3,5,7,9}.
因此可以用样本空间Ω={0,1,2,3,4,5,6,7,8,9}的子集{1,3,5,7,9}表示随机事件A.类似地,可以用样本空间的子集{0,3,6,9}表示随机事件“球的号码为3的倍数”
随机事件
随机事件:一般地,随机试验中的每个随机事件都可以用这个试验的样本空间的子集来表示.我们将样本空间Ω的子集称为随机事件,简称事件,一般用大写字母A,B,…表示.
基本事件:只包含一个样本点的事件称为基本事件.
必然事件:包含了所有样本点,在每次试验中总有一个样本点的事件发生,即Ω总会发生.
不可能事件:不包含任何样本点的事件,在每次实验中都不会发生.
1.指出下列事件是必然事件,不可能事件,还是随机事件:
(1)某地1月1日刮西北风;
(2)手电筒的电池没电,灯泡发亮;
(3)一个电影院某天的上座率超过50%。
(4)如果a>b,那么a一b>0;
(5)从分别标有数字l,2,3,4,5的5张标签中任取一张,得到4号签;
(6)随机选取一个实数x,得|x|<0.
随机事件
不可能事件
随机事件
必然事件
随机事件
不可能事件
例如图,一个电路中有A,B,C三个电器元件,每个元件可能正常,也可能失效.把这个电路是否为通路看成是一个随机现象,观察这个电路中各元件是否正常.
(1)写出试验的样本空间;
(2)用集合表示下列事件:
M=“恰好两个元件正常”;
N=“电路是通路”;
T=“电路是断路”.
解:(1)分别用x1,x2和x3表示元件A,B和C的可能状态,则这个电路的工作状态可用(x1,x2,x3)表示.进一步地,用1表示元件的“正常”状态,用0表示“失效”状态,
则样本空间Ω={(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1)}.
(2)“恰好两个元件正常”等价于(x1,x2,x3) ∈Ω,且x1,x2,x3中恰有两个为1,
所以M={(1,1,0),(1,0,1),(0,1,1)}.
“电路是通路”等价于(x1,x2,x3) ∈Ω ,x1=1,且x2,x3中至少有一个是1,所以N={(1,1,0),(1,0,1),(1,1,1)}。
同理,“电路是断路”等价于(x1,x2,x3) ∈Ω,x1=0,或x1=1,x2=x3=0.所以T={(0,0,0),(0,1,0),(0,0,1),(0,1,1),(1,0,0)}.
如图,还可以借助树状图帮助我们列出试验的所有可能结果.
类题通法
(1)用样本点表示随机事件,首先弄清试验的样本空间,不重不漏列出所有的样本点.然后找出满足随机事件要求的样本点,从而用这些样本点组成的集合表示随机事件.
(2)随机事件可以用文字表示,也可以将事件表示为样本空间的子集,后者反映了事件的本质,且更便于今后计算事件发生的概率.
1
2
3
4
易错提醒
核心知识
有限样本空间与随机事件
方法总结
核心素养
在列举样本点时注意分类思想的运用,做到不重不漏
数学抽象:形成随机事件的概念的过程
数学建模:写出样本空间中的样本点,分析随机试验
随机试验
样本空间
确定样本空间的方法:
通过列表、画树状图等方法列举样本点
随机事件
样本点
特点
基本事件
概念
有限样本空间
必然事件
不可能事件
1.从6个篮球、2个排球中任选3个球,则下列事件中,不可能事件是( )
A.3个都是篮球 B.至少有1个是排球
C.3个都是排球 D.至少有1个是篮球
解析:根据题意,从6个篮球、2个排球中任选3个球,四个选项都是随机事件,进一步C是不可能事件,D是必然事件.
C
解析 在所给条件下,①是必然事件;②是随机事件;③是必然事件;④是不可能事件;⑤是随机事件.
B
3.先后掷两枚质地均匀的骰子,骰子朝上的面的点数分别为x,y,则事件:log2xy=1包含的样本点有________.
解析 先后掷两枚质地均匀的骰子,骰子朝上的面的点数有36种结果.解方程log2xy=1得y=2x,
则符合条件的样本点有
(1,2),(2,4),(3,6).
(x,y) 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
4. 在12件同类产品中,有10件正品,2件次品,从中任意抽出3件,下列事件中:① 3件都是正品;② 至少有1件是次品;③ 3件都是次品;④ 至少有1件是正品.其中随机事件有________,必然事件有________,不可能事件有________.(填上相应的序号)
【解析】抽出的3件可能都是正品,也可能不都是正品,故①②是随机事件;这12件产品中共有2件次品,那么抽出的3件不可能都是次品,其中至少有1件是正品,故③是不可能事件,④是必然事件.
①②
④
③
追赶时间的人,生活就会宠爱他;放弃时间的人,生活就会冷落他.
第十章 概率
概率论的产生和发展
传说早在1654年,有一个赌徒梅累向当时的数学家帕斯卡提出一个使他苦恼了很久的问题:“两个赌徒约定谁先赢满5局,谁就获得全部赌金。赌了半天, A赢了4局, B赢了3局,时间很晚了,他们都不想再赌下去了。那么,这个钱应该怎么分才理?
这个问题让帕斯卡苦苦思索了三年,三年后也就是1657年,
荷兰著名的数学家惠更斯企图自己解决这一问题,结果写成了
《论赌博中的计算》一书,这就是概率论最早的一部著作。
1.了解随机试验、样本空间的概念.
2.通过实例,了解必然事件、不可能事件与随机事件的含义.
1.数学抽象:随机试验、样本空间、样本容量的概念.
2.数据分析:判断必然事件、不可能事件与随机事件.
3.数学运算:写出事件的样本空间.
微课1:有限样本空间
我们把对随机现象的实现和对它的观察称为随机试验(random experiment),简称试验,常用字母E表示.我们感兴趣的是具有以下特点的随机试验:
(1)试验可以在相同条件下重复进行;
(2)试验的所有可能结果是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现
哪一个结果.
可重复性
可预知性
随机性
思考1:体育彩票摇奖时,将10个质地和大小完全相同、分别标号0,1,2,…,9的球放入摇奖器中,经过充分搅拌后摇出一个球,观察这个球的号码,这个随机试验共有多少个可能结果?如何表示这些结果?
共有10种可能结果.
所有可能结果可用集合表示为:{0,1,2,3,4,5,6,7,8,9}
样本点与样本空间
(1)样本点:随机试验E的每个可能的基本结果称为样本点;
(2)样本空间:全体样本点的集合称为试验E的样本空间.
一般地,用Ω表示样本空间,用ω表示样本点;
(3)有限样本空间:如果一个随机试验有n个可能结果ω1,ω2,…, ωn,
则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
解:因为落地时只有正面朝上和反面朝上两个可能结果,所以试
验的样本空间可以表示为Ω =(正面朝上,反面朝上),如果
用h表示“正面朝上”,t表示“反面朝上”,则样本空间
Ω ={h,t}.
典例解析
例1.抛掷一枚硬币,观察它落地时哪一面朝上,写出试验的样本空间。
例2 .抛掷一枚骰子(touzi),观察它落地时朝上的面的点数,写出试验的
样本空间.
解:用i表示朝上面的“点数为i”,
因为落地时朝上面的点数有1,2,3,4,5,6共6个可能的基本结果,
所以试验的样本空间可以表示为Ω ={1,2,3,4,5,6}.
解法一:掷两枚硬币,第一枚硬币可能的基本结果用x表示,
第二枚硬币可能的基本结果用y表示,
那么试验的样本点可用(x,y)表示.于是,试验的样本空间
Ω ={(正面,正面),(正面,反面),(反面,正面),(反面,反面)}
例3.抛掷两枚硬币,观察它们落地时朝上的面的情况,写出试验的样
本空间
解法二:如果我们用1表示硬币“正面朝上”,用0表示硬币“反面朝 上”,那么样本空间还可以简单表示为Ω={(1,1),(1,0),(0,1),(0,0)}.
如图所示,画树状图可以帮助我们理
解例3的解答过程.
类题通法
(1)如何确定试验的样本空间?
提示:要考虑周全,应想到试验的所有可能的结果,避免发生遗漏和出现多余或者重复的结果.
(2)写试验的样本空间要注意些什么?
提示:确定试验的样本空间就是写出试验的所有可能的结果,并写成Ω={ω1,ω2,…,ωn}的形式.
解:(1)Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),
(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}.
(2)样本点的总数为16.
(3)“x+y=5”包含以下4个样本点:(1,4),(2,3),(3,2),(1,4);
“x<3且y>1”包含以下6个样本点:(1,2),(1,3),(1,4),(2,2),(2,3),(2,4).
(4)“xy=4”包含以下3个样本点:(1,4),(2,2),(4,1);
“x=y”包含以下4个样本点:(1,1),(2,2),(3,3),(4,4).
微课2: 随机事件
思考: 在体育彩票摇号实验中,摇出“球的号码是奇数”是随机事件吗?摇出“球的号码为3的倍数”是否也是随机事件?如果用集合的形式来表示它们,那么这些集合与样本空间有什么关系?
显然,“球的号码为奇数”和“球的号码为3的倍数”都是随机事件.
我们用A表示随机事件“球的号码为奇数”,则A发生,当且仅当摇出的号码为1,3,5,7,9之一,即事件A发生等价于摇出的号码属于集合{1,3,5,7,9}.
因此可以用样本空间Ω={0,1,2,3,4,5,6,7,8,9}的子集{1,3,5,7,9}表示随机事件A.类似地,可以用样本空间的子集{0,3,6,9}表示随机事件“球的号码为3的倍数”
随机事件
随机事件:一般地,随机试验中的每个随机事件都可以用这个试验的样本空间的子集来表示.我们将样本空间Ω的子集称为随机事件,简称事件,一般用大写字母A,B,…表示.
基本事件:只包含一个样本点的事件称为基本事件.
必然事件:包含了所有样本点,在每次试验中总有一个样本点的事件发生,即Ω总会发生.
不可能事件:不包含任何样本点的事件,在每次实验中都不会发生.
1.指出下列事件是必然事件,不可能事件,还是随机事件:
(1)某地1月1日刮西北风;
(2)手电筒的电池没电,灯泡发亮;
(3)一个电影院某天的上座率超过50%。
(4)如果a>b,那么a一b>0;
(5)从分别标有数字l,2,3,4,5的5张标签中任取一张,得到4号签;
(6)随机选取一个实数x,得|x|<0.
随机事件
不可能事件
随机事件
必然事件
随机事件
不可能事件
例如图,一个电路中有A,B,C三个电器元件,每个元件可能正常,也可能失效.把这个电路是否为通路看成是一个随机现象,观察这个电路中各元件是否正常.
(1)写出试验的样本空间;
(2)用集合表示下列事件:
M=“恰好两个元件正常”;
N=“电路是通路”;
T=“电路是断路”.
解:(1)分别用x1,x2和x3表示元件A,B和C的可能状态,则这个电路的工作状态可用(x1,x2,x3)表示.进一步地,用1表示元件的“正常”状态,用0表示“失效”状态,
则样本空间Ω={(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1)}.
(2)“恰好两个元件正常”等价于(x1,x2,x3) ∈Ω,且x1,x2,x3中恰有两个为1,
所以M={(1,1,0),(1,0,1),(0,1,1)}.
“电路是通路”等价于(x1,x2,x3) ∈Ω ,x1=1,且x2,x3中至少有一个是1,所以N={(1,1,0),(1,0,1),(1,1,1)}。
同理,“电路是断路”等价于(x1,x2,x3) ∈Ω,x1=0,或x1=1,x2=x3=0.所以T={(0,0,0),(0,1,0),(0,0,1),(0,1,1),(1,0,0)}.
如图,还可以借助树状图帮助我们列出试验的所有可能结果.
类题通法
(1)用样本点表示随机事件,首先弄清试验的样本空间,不重不漏列出所有的样本点.然后找出满足随机事件要求的样本点,从而用这些样本点组成的集合表示随机事件.
(2)随机事件可以用文字表示,也可以将事件表示为样本空间的子集,后者反映了事件的本质,且更便于今后计算事件发生的概率.
1
2
3
4
易错提醒
核心知识
有限样本空间与随机事件
方法总结
核心素养
在列举样本点时注意分类思想的运用,做到不重不漏
数学抽象:形成随机事件的概念的过程
数学建模:写出样本空间中的样本点,分析随机试验
随机试验
样本空间
确定样本空间的方法:
通过列表、画树状图等方法列举样本点
随机事件
样本点
特点
基本事件
概念
有限样本空间
必然事件
不可能事件
1.从6个篮球、2个排球中任选3个球,则下列事件中,不可能事件是( )
A.3个都是篮球 B.至少有1个是排球
C.3个都是排球 D.至少有1个是篮球
解析:根据题意,从6个篮球、2个排球中任选3个球,四个选项都是随机事件,进一步C是不可能事件,D是必然事件.
C
解析 在所给条件下,①是必然事件;②是随机事件;③是必然事件;④是不可能事件;⑤是随机事件.
B
3.先后掷两枚质地均匀的骰子,骰子朝上的面的点数分别为x,y,则事件:log2xy=1包含的样本点有________.
解析 先后掷两枚质地均匀的骰子,骰子朝上的面的点数有36种结果.解方程log2xy=1得y=2x,
则符合条件的样本点有
(1,2),(2,4),(3,6).
(x,y) 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
4. 在12件同类产品中,有10件正品,2件次品,从中任意抽出3件,下列事件中:① 3件都是正品;② 至少有1件是次品;③ 3件都是次品;④ 至少有1件是正品.其中随机事件有________,必然事件有________,不可能事件有________.(填上相应的序号)
【解析】抽出的3件可能都是正品,也可能不都是正品,故①②是随机事件;这12件产品中共有2件次品,那么抽出的3件不可能都是次品,其中至少有1件是正品,故③是不可能事件,④是必然事件.
①②
④
③
追赶时间的人,生活就会宠爱他;放弃时间的人,生活就会冷落他.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
