人教版数学八年级下册 18.2.1矩形课件(共33张ppt)
文档属性
| 名称 | 人教版数学八年级下册 18.2.1矩形课件(共33张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 17:26:37 | ||
图片预览









文档简介
(共33张PPT)
矩形
学习目标:
1.理解矩形的概念,明确矩形与平行四边形的区别
与联系;
2.探索并证明矩形的性质,会用矩形的性质解决简
单的问题;
3.探索并掌握“直角三角形斜边上的中线等于斜边
的一半”这个定理.
学习重点:
矩形区别于一般平行四边形的性质的探索、证明和应用.
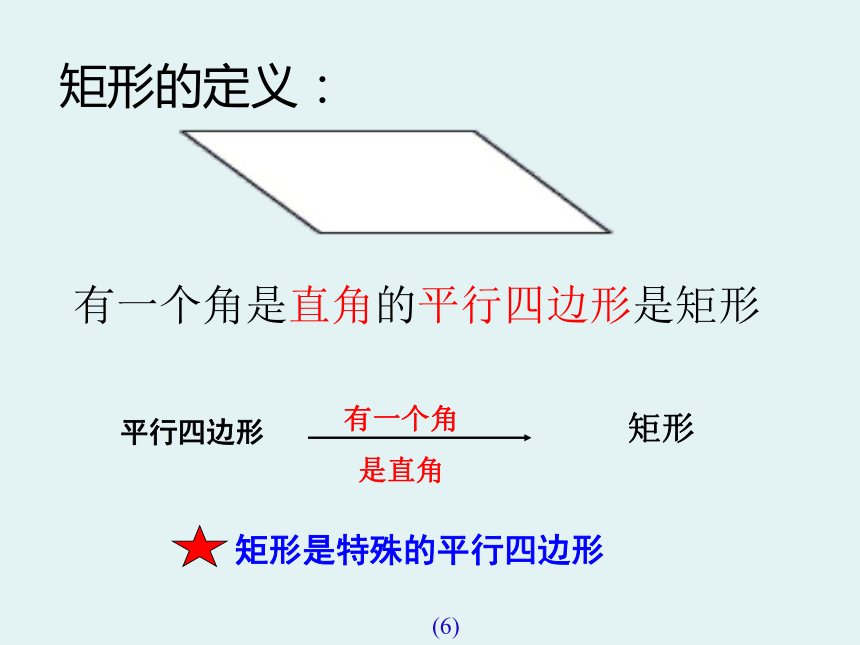
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
(6)
生活中有很多具有矩形形象的物品,你能举出一些例子吗?
说一说
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等 ,邻角互补
对角线互相平分
矩形的一般性质:
思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?下面请童孩们在草稿本上分别画一个平行四边形和一个矩形仔细研究一下,看看你还能得出哪些结论?
结论1:矩形的四个角都是直角.
结论2:矩形的对角线相等.
A
B
C
D
结论3:(对称性)矩形是轴对称图形,它有两条对称轴。
1:矩形的四个角都是直角
D
C
B
A
命题
性质
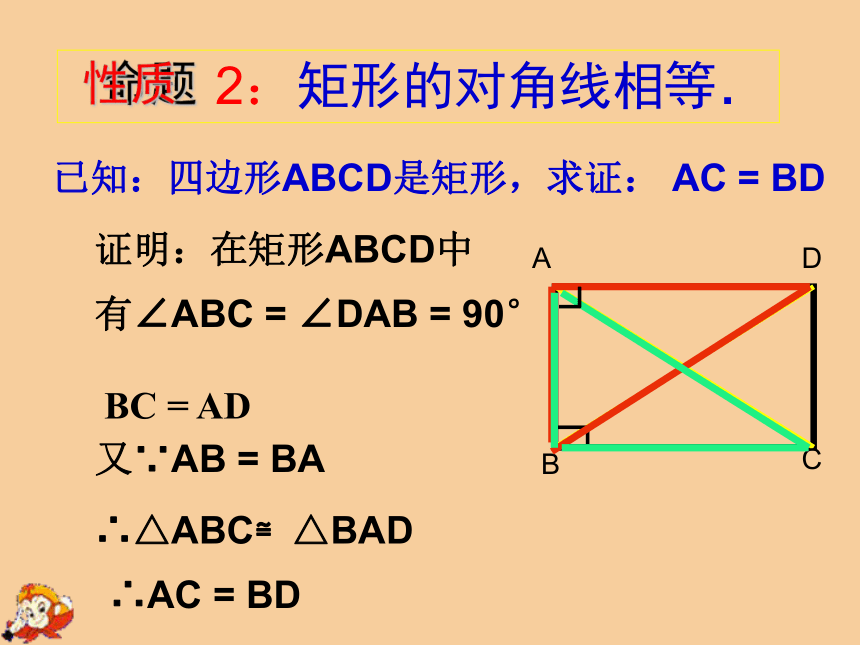
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明:在矩形ABCD中
有∠ABC = ∠DAB = 90°
BC = AD
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
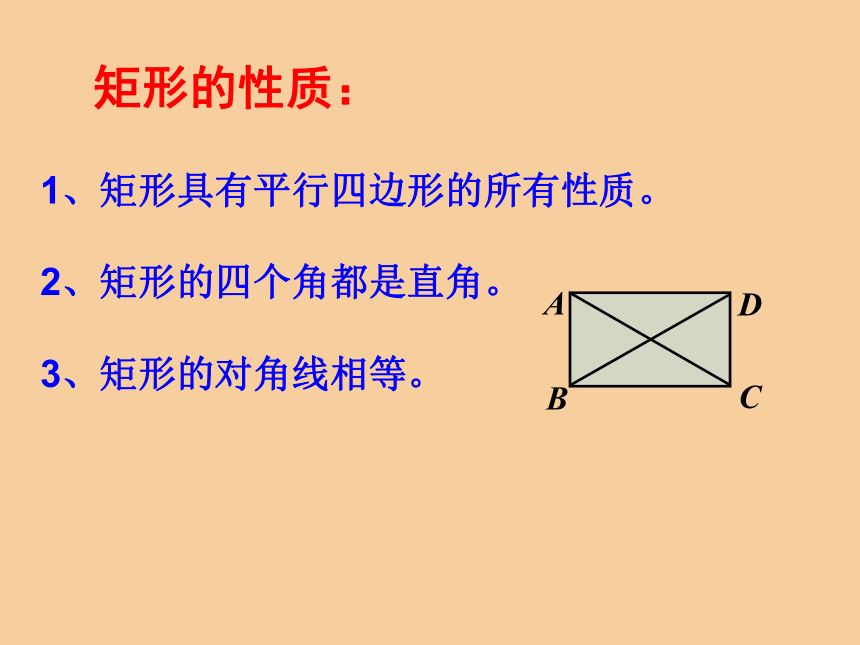
矩形的性质:
1、矩形具有平行四边形的所有性质。
2、矩形的四个角都是直角。
3、矩形的对角线相等。
B
C
D
A
边
角
对角线
平行
四边形
矩形
对边平行且相等
对角相等
邻角互补
对角线
互相平分
对边平行
且相等
四个角
都是直角
对角线互相
平分且相等
类比总结
矩形特有
的性质
已知矩形ABCD,请找出所有的直角三角形和等腰三角形.
A
B
C
D
O
矩形的问题通常转化为直角三角形或等腰三角形来解决.
Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC
△AOD和 △COB
△DOC和 △BOA
◆ 两对全等的等腰三角形.
◆ 四个全等的直角三角形.
观察
你在矩形中发现了哪些基本图形?
A
B
C
O
得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
在Rt△ABC中, BO= AC
探索新知
在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系
B
D
C
A
O
A
C
B
O
D
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线
若∠C=30°,AB=5㎝,则AC= ㎝,BD= ㎝,
5
10
小试身手
公平,因为OA=OC=OB=OD
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
1.为了庆祝五一劳动节,二圣学校八年级一班同学要在操场上布置一个矩形的花坛,计划用“杜鹃花”摆成两条对角线,如果一条对角线用了38盆“杜鹃花”,还需要从花房里运来多少盆“杜鹃花”?为什么?如果一条对角线用了49盆呢?为什么?
生活链接
挑战开始
矩形具有而一般平行四边形不
具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
C
营中热身
(23)
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
营中寻宝
(24)
D
C
B
A
┓
4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线
(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.
6
5
10
营中寻宝
(25)
请 选 择
6
2
4
3
5
1
挑战第一关
进入第二关
进入第三关
通关小 结
(快速问答)
营中挑战
1、矩形的定义中有两个条件:
一是:
二是:
。
。
有一个角是直角
是一个平行四边形
(请你的同桌回答)
2、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分
A
(请你回答)
4、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
A
C
B
O
。
8
(你请她回答)
3、如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为
A
B
C
D
O
。
16
(请你的邻桌回答)
5、矩形是轴对称图形吗 它有几条对称轴?
(你请好朋友回答)
是
两条
6、下列说法错误的是( )
(A)矩形的对角线互相平分。
(B)矩形的对角线相等。
(C)有一个角是直角的四边形是矩形。
(D)有一个角是直角的平行四边形叫做矩形。
(请你回答)
C
练习:如图,矩形ABCD的两条对角线相交于点O,
且∠AOB=60°,AB=4 cm.求矩形对角线的长.
A
B
C
D
O
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分。
∴OA=OB.
又∠AOB=60°,
∴△OAB是等边三角形。
∴OA=AB=4.
∴AC=BD=2AO=8.
挑战第二关:运用性质 解决问题
练习:如图,在矩形ABCD中,AE平分∠BAD,交
BC于点E,ED=5,EC=3,求矩形的周长及对角线的长。
A
B
C
D
E
3
5
4
4
4
7
挑战第三关
谈谈你在这节课中学到了什么?有哪些收获?
课堂小结:
直角三角形性质:直角三角形斜边上的中线
等于斜边的一半.
矩形是轴对称图形,有两条对称轴,连接对边中点
的直线是它的两条对称轴.
课堂小结
矩形
1、具有平行四边形的所有性质;
2、矩形的四个角都是直角;
3、矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
矩形
学习目标:
1.理解矩形的概念,明确矩形与平行四边形的区别
与联系;
2.探索并证明矩形的性质,会用矩形的性质解决简
单的问题;
3.探索并掌握“直角三角形斜边上的中线等于斜边
的一半”这个定理.
学习重点:
矩形区别于一般平行四边形的性质的探索、证明和应用.
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
(6)
生活中有很多具有矩形形象的物品,你能举出一些例子吗?
说一说
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等 ,邻角互补
对角线互相平分
矩形的一般性质:
思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?下面请童孩们在草稿本上分别画一个平行四边形和一个矩形仔细研究一下,看看你还能得出哪些结论?
结论1:矩形的四个角都是直角.
结论2:矩形的对角线相等.
A
B
C
D
结论3:(对称性)矩形是轴对称图形,它有两条对称轴。
1:矩形的四个角都是直角
D
C
B
A
命题
性质
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明:在矩形ABCD中
有∠ABC = ∠DAB = 90°
BC = AD
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
矩形的性质:
1、矩形具有平行四边形的所有性质。
2、矩形的四个角都是直角。
3、矩形的对角线相等。
B
C
D
A
边
角
对角线
平行
四边形
矩形
对边平行且相等
对角相等
邻角互补
对角线
互相平分
对边平行
且相等
四个角
都是直角
对角线互相
平分且相等
类比总结
矩形特有
的性质
已知矩形ABCD,请找出所有的直角三角形和等腰三角形.
A
B
C
D
O
矩形的问题通常转化为直角三角形或等腰三角形来解决.
Rt△ADC、 Rt△DCB、
Rt△DAB、 Rt△ABC
△AOD和 △COB
△DOC和 △BOA
◆ 两对全等的等腰三角形.
◆ 四个全等的直角三角形.
观察
你在矩形中发现了哪些基本图形?
A
B
C
O
得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
在Rt△ABC中, BO= AC
探索新知
在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系
B
D
C
A
O
A
C
B
O
D
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线
若∠C=30°,AB=5㎝,则AC= ㎝,BD= ㎝,
5
10
小试身手
公平,因为OA=OC=OB=OD
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
1.为了庆祝五一劳动节,二圣学校八年级一班同学要在操场上布置一个矩形的花坛,计划用“杜鹃花”摆成两条对角线,如果一条对角线用了38盆“杜鹃花”,还需要从花房里运来多少盆“杜鹃花”?为什么?如果一条对角线用了49盆呢?为什么?
生活链接
挑战开始
矩形具有而一般平行四边形不
具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
C
营中热身
(23)
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
营中寻宝
(24)
D
C
B
A
┓
4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线
(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.
6
5
10
营中寻宝
(25)
请 选 择
6
2
4
3
5
1
挑战第一关
进入第二关
进入第三关
通关小 结
(快速问答)
营中挑战
1、矩形的定义中有两个条件:
一是:
二是:
。
。
有一个角是直角
是一个平行四边形
(请你的同桌回答)
2、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分
A
(请你回答)
4、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
A
C
B
O
。
8
(你请她回答)
3、如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为
A
B
C
D
O
。
16
(请你的邻桌回答)
5、矩形是轴对称图形吗 它有几条对称轴?
(你请好朋友回答)
是
两条
6、下列说法错误的是( )
(A)矩形的对角线互相平分。
(B)矩形的对角线相等。
(C)有一个角是直角的四边形是矩形。
(D)有一个角是直角的平行四边形叫做矩形。
(请你回答)
C
练习:如图,矩形ABCD的两条对角线相交于点O,
且∠AOB=60°,AB=4 cm.求矩形对角线的长.
A
B
C
D
O
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分。
∴OA=OB.
又∠AOB=60°,
∴△OAB是等边三角形。
∴OA=AB=4.
∴AC=BD=2AO=8.
挑战第二关:运用性质 解决问题
练习:如图,在矩形ABCD中,AE平分∠BAD,交
BC于点E,ED=5,EC=3,求矩形的周长及对角线的长。
A
B
C
D
E
3
5
4
4
4
7
挑战第三关
谈谈你在这节课中学到了什么?有哪些收获?
课堂小结:
直角三角形性质:直角三角形斜边上的中线
等于斜边的一半.
矩形是轴对称图形,有两条对称轴,连接对边中点
的直线是它的两条对称轴.
课堂小结
矩形
1、具有平行四边形的所有性质;
2、矩形的四个角都是直角;
3、矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
