第五讲 探索三角形全等的条件—SSS,SAS(基础讲解)(含解析)
文档属性
| 名称 | 第五讲 探索三角形全等的条件—SSS,SAS(基础讲解)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五讲 探索三角形全等的条件—SSS/SAS
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
【知识总结】
一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果=AB,=AC,=BC,则△ABC≌△.
( http: / / www.21cnjy.com / )
二、全等三角形判定2——“边角边”
1. 全等三角形判定2——“边角边”
两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
( http: / / www.21cnjy.com / )
【注】:
如图,如果AB = ,∠A=∠,AC = ,则△ABC≌△. 注意:这里的角,指的是两组对应边的夹角.21教育网
2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.
如图,△ABC与△ABD ( http: / / www.21cnjy.com )中,AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.21·cn·jy·com
( http: / / www.21cnjy.com / )
【典型例题】
【类型】一、全等三角形的判定1——“边边边”
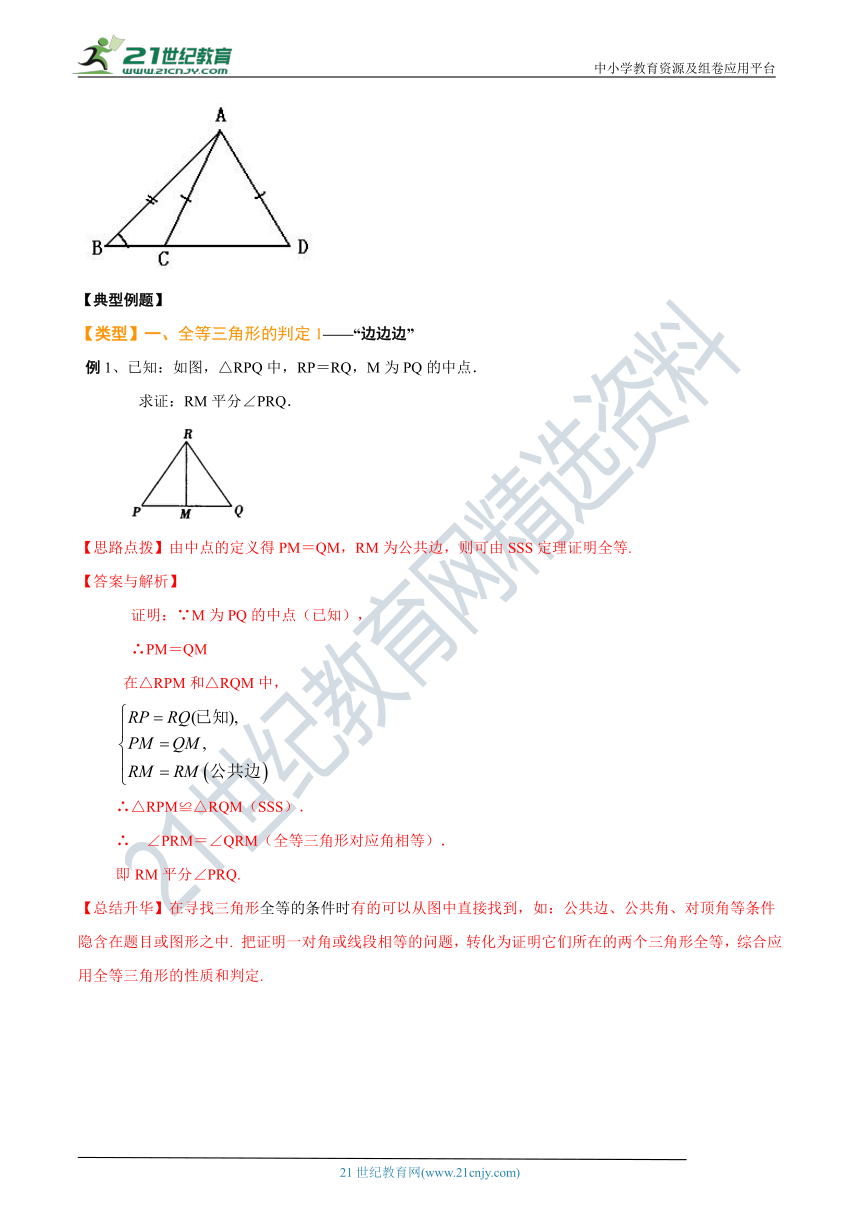
例1、已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
求证:RM平分∠PRQ.
( http: / / www.21cnjy.com / )
【思路点拨】由中点的定义得PM=QM,RM为公共边,则可由SSS定理证明全等.
【答案与解析】
证明:∵M为PQ的中点(已知),
∴PM=QM
在△RPM和△RQM中,
∴△RPM≌△RQM(SSS).
∴ ∠PRM=∠QRM(全等三角形对应角相等).
即RM平分∠PRQ.
【总结升华】在寻找三角形全等的条件时 ( http: / / www.21cnjy.com )有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.21cnjy.com
【类型】二、全等三角形的判 ( http: / / www.21cnjy.com )定2——“边角边”
例2、 如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.
( http: / / www.21cnjy.com / )
【思路点拨】根据等腰直角三角形的性质得出CE=CD,BC=AC,再利用全等三角形的判定证明即可.
【答案与解析】
证明:∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中,
∴△CDA≌△CEB.
【总结升华】本题考查了全等三角形的判定, ( http: / / www.21cnjy.com )熟记等腰直角三角形的性质是解题的关键,同时注意证明角等的方法之一:利用等式的性质,等量加等量,还是等量.2·1·c·n·j·y
【训练】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.求证:△ACD≌△BCE.
( http: / / www.21cnjy.com / )
【答案】证明:∵C是线段AB的中点,
∴AC=BC,
∵CD平分∠ACE,CE平分∠BCD,
∴∠ACD=∠ECD,∠BCE=∠ECD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).
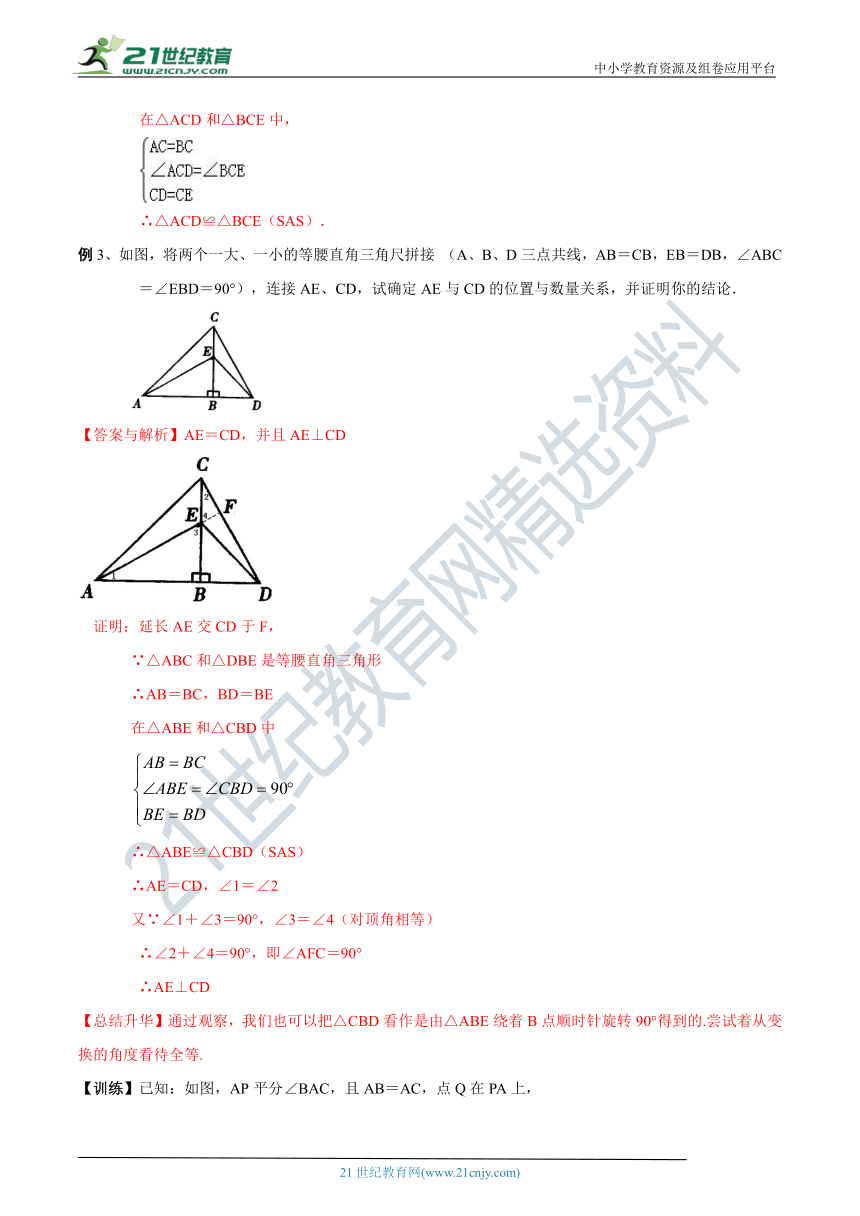
例3、如图,将两个一大、一小的等腰 ( http: / / www.21cnjy.com )直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
( http: / / www.21cnjy.com / )
【答案与解析】AE=CD,并且AE⊥CD
( http: / / www.21cnjy.com / )
证明:延长AE交CD于F,
∵△ABC和△DBE是等腰直角三角形
∴AB=BC,BD=BE
在△ABE和△CBD中
∴△ABE≌△CBD(SAS)
∴AE=CD,∠1=∠2
又∵∠1+∠3=90°,∠3=∠4(对顶角相等)
∴∠2+∠4=90°,即∠AFC=90°
∴AE⊥CD
【总结升华】通过观察,我们也可以把△CBD看作是由△ABE绕着B点顺时针旋转90°得到的.尝试着从变换的角度看待全等.21世纪教育网版权所有
【训练】已知:如图,AP平分∠BAC,且AB=AC,点Q在PA上,
求证:QC=QB
( http: / / www.21cnjy.com / )
【答案】
证明:∵ AP平分∠BAC
∴∠BAP=∠CAP
在△ABQ与△ACQ中
∵
∴△ABQ≌△ACQ(SAS)【来源:21·世纪·教育·网】
∴ QC=QB
【类型】三、全等三角形判定的实际应用
例4、 如图,点D为码头,A,B两个灯 ( http: / / www.21cnjy.com )塔与码头的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的角平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
【思路点拨】只要证明轮船与D点的连线平分∠A ( http: / / www.21cnjy.com )DB就说明轮船没有偏离航线,也就是证明∠ADC=∠BDC.要证明角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.21·世纪*教育网
【答案与解析】
解:此时轮船没有偏离航线.
理由:由题意知:DA=DB,AC=BC,
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SSS),
∴∠ADC=∠BDC,
即DC为∠ADB的角平分线,
∴此时轮船没有偏离航线.
【总结升华】本题考查了全等 ( http: / / www.21cnjy.com )三角形的应用,解答本题的关键是:根据条件设计三角形全等,巧妙地借助两个三角形全等,寻找对应角相等.要学会把实际问题转化为数学问题来解决.www-2-1-cnjy-com
【训练】工人师傅经常利用角尺平分一个任意 ( http: / / www.21cnjy.com )角,如图所示,∠AOB是一个任意角,在边OA,边OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D、E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线,你能先说明△OPE与△OPD全等,再说明OP平分∠AOB吗?
( http: / / www.21cnjy.com / )
【答案】证明: 在△OPE与△OPD中
∵
∴ △OPE≌△OPD (SSS)
∴ ∠EOP=∠DOP(全等三角形对应角相等)
∴ OP平分∠AOB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第五讲 探索三角形全等的条件—SSS/SAS
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
【知识总结】
一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果=AB,=AC,=BC,则△ABC≌△.
( http: / / www.21cnjy.com / )
二、全等三角形判定2——“边角边”
1. 全等三角形判定2——“边角边”
两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
( http: / / www.21cnjy.com / )
【注】:
如图,如果AB = ,∠A=∠,AC = ,则△ABC≌△. 注意:这里的角,指的是两组对应边的夹角.21教育网
2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.
如图,△ABC与△ABD ( http: / / www.21cnjy.com )中,AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.21·cn·jy·com
( http: / / www.21cnjy.com / )
【典型例题】
【类型】一、全等三角形的判定1——“边边边”
例1、已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
求证:RM平分∠PRQ.
( http: / / www.21cnjy.com / )
【思路点拨】由中点的定义得PM=QM,RM为公共边,则可由SSS定理证明全等.
【答案与解析】
证明:∵M为PQ的中点(已知),
∴PM=QM
在△RPM和△RQM中,
∴△RPM≌△RQM(SSS).
∴ ∠PRM=∠QRM(全等三角形对应角相等).
即RM平分∠PRQ.
【总结升华】在寻找三角形全等的条件时 ( http: / / www.21cnjy.com )有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.21cnjy.com
【类型】二、全等三角形的判 ( http: / / www.21cnjy.com )定2——“边角边”
例2、 如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.
( http: / / www.21cnjy.com / )
【思路点拨】根据等腰直角三角形的性质得出CE=CD,BC=AC,再利用全等三角形的判定证明即可.
【答案与解析】
证明:∵△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴CE=CD,BC=AC,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
在△CDA与△CEB中,
∴△CDA≌△CEB.
【总结升华】本题考查了全等三角形的判定, ( http: / / www.21cnjy.com )熟记等腰直角三角形的性质是解题的关键,同时注意证明角等的方法之一:利用等式的性质,等量加等量,还是等量.2·1·c·n·j·y
【训练】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.求证:△ACD≌△BCE.
( http: / / www.21cnjy.com / )
【答案】证明:∵C是线段AB的中点,
∴AC=BC,
∵CD平分∠ACE,CE平分∠BCD,
∴∠ACD=∠ECD,∠BCE=∠ECD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).
例3、如图,将两个一大、一小的等腰 ( http: / / www.21cnjy.com )直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
( http: / / www.21cnjy.com / )
【答案与解析】AE=CD,并且AE⊥CD
( http: / / www.21cnjy.com / )
证明:延长AE交CD于F,
∵△ABC和△DBE是等腰直角三角形
∴AB=BC,BD=BE
在△ABE和△CBD中
∴△ABE≌△CBD(SAS)
∴AE=CD,∠1=∠2
又∵∠1+∠3=90°,∠3=∠4(对顶角相等)
∴∠2+∠4=90°,即∠AFC=90°
∴AE⊥CD
【总结升华】通过观察,我们也可以把△CBD看作是由△ABE绕着B点顺时针旋转90°得到的.尝试着从变换的角度看待全等.21世纪教育网版权所有
【训练】已知:如图,AP平分∠BAC,且AB=AC,点Q在PA上,
求证:QC=QB
( http: / / www.21cnjy.com / )
【答案】
证明:∵ AP平分∠BAC
∴∠BAP=∠CAP
在△ABQ与△ACQ中
∵
∴△ABQ≌△ACQ(SAS)【来源:21·世纪·教育·网】
∴ QC=QB
【类型】三、全等三角形判定的实际应用
例4、 如图,点D为码头,A,B两个灯 ( http: / / www.21cnjy.com )塔与码头的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的角平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
【思路点拨】只要证明轮船与D点的连线平分∠A ( http: / / www.21cnjy.com )DB就说明轮船没有偏离航线,也就是证明∠ADC=∠BDC.要证明角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.21·世纪*教育网
【答案与解析】
解:此时轮船没有偏离航线.
理由:由题意知:DA=DB,AC=BC,
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SSS),
∴∠ADC=∠BDC,
即DC为∠ADB的角平分线,
∴此时轮船没有偏离航线.
【总结升华】本题考查了全等 ( http: / / www.21cnjy.com )三角形的应用,解答本题的关键是:根据条件设计三角形全等,巧妙地借助两个三角形全等,寻找对应角相等.要学会把实际问题转化为数学问题来解决.www-2-1-cnjy-com
【训练】工人师傅经常利用角尺平分一个任意 ( http: / / www.21cnjy.com )角,如图所示,∠AOB是一个任意角,在边OA,边OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D、E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线,你能先说明△OPE与△OPD全等,再说明OP平分∠AOB吗?
( http: / / www.21cnjy.com / )
【答案】证明: 在△OPE与△OPD中
∵
∴ △OPE≌△OPD (SSS)
∴ ∠EOP=∠DOP(全等三角形对应角相等)
∴ OP平分∠AOB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
