4.1.1实数指数幂及其运算 课件(共50张PPT)
文档属性
| 名称 | 4.1.1实数指数幂及其运算 课件(共50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 841.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览








文档简介
(共50张PPT)
实数指数幂及其运算
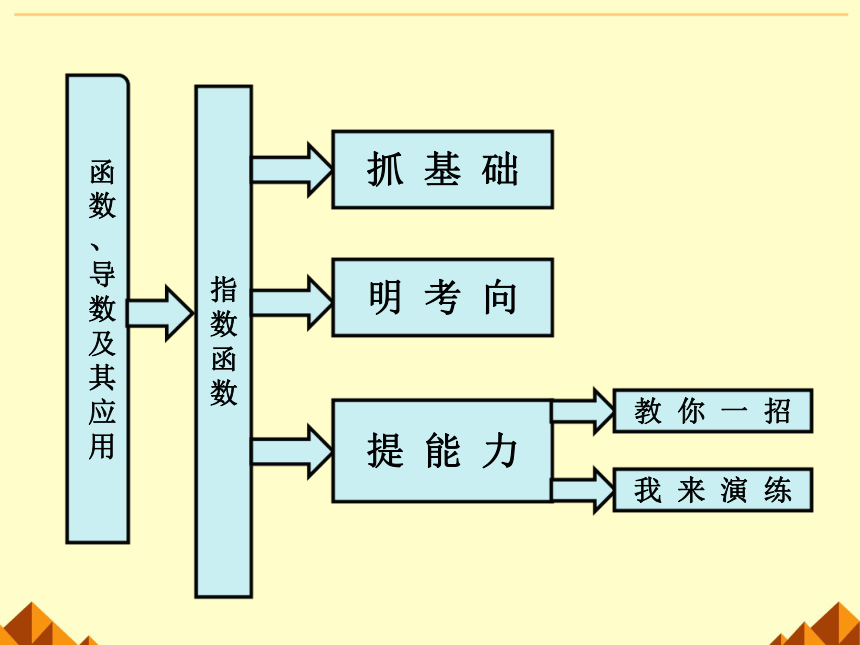
函数
、导数及其应用
指数函数
抓 基 础
明 考 向
提 能 力
教 你 一 招
我 来 演 练
[备考方向要明了]
考 什 么
1.了解指数函数模型的实际背景.
2.理解有理数指数幂的含义,了解实数指数幂的意义,
掌握幂的运算.
3.理解指数幂的概念,理解指数函数的单调性,会解决
与指数函数性质有关的问题.
怎 么 考
1.指数函数的概念、图象与性质是近几年高考的热点.
2.通过具体问题考查指数函数的图象与性质,或利用指数函
数的图象与性质解决一些实际问题是重点,也是难点,同
时考查分类讨论思想和数形结合思想.
3.题型以选择题和填空题为主,与其他知识点交汇则以解答
题的形式出现.
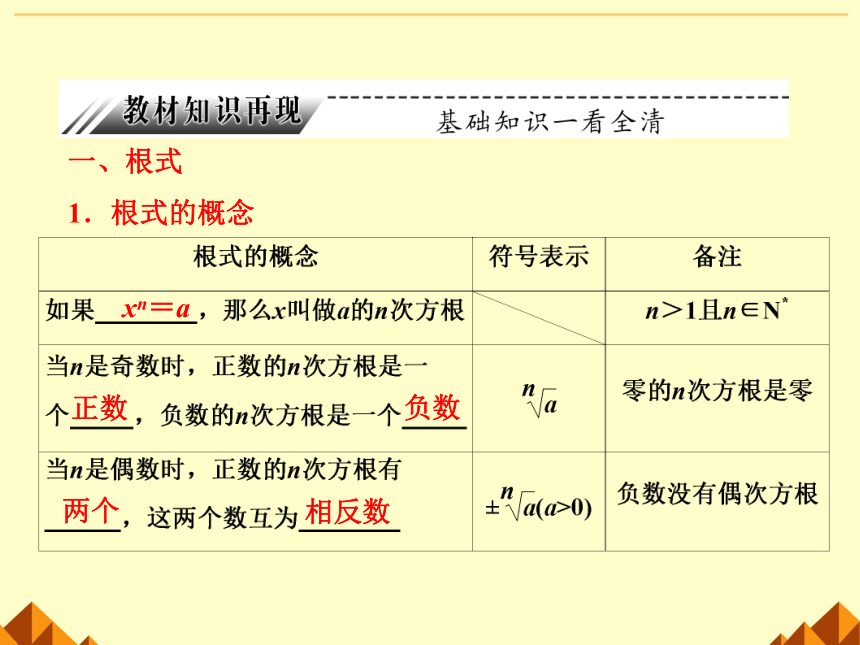
一、根式
1.根式的概念
xn=a
正数
负数
两个
相反数
2.两个重要公式
a
-a
a
a
0
没有意义
2.有理数指数幂的性质
(1)aras= (a>0,r,s∈Q);
(2)(ar)s= (a>0,r,s∈Q);
(3)(ab)r= (a>0,b>0,r∈Q).
ar+s
ars
arbr
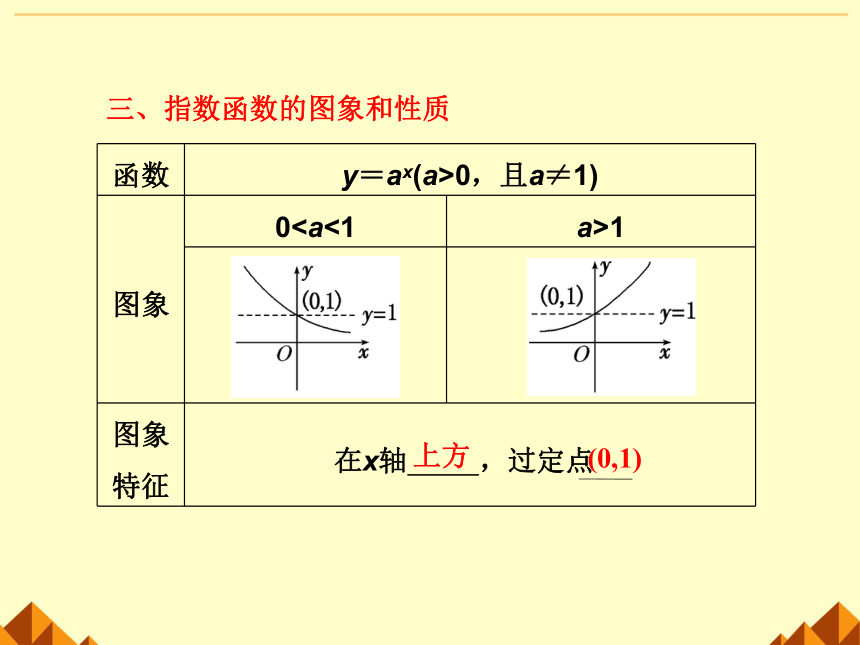
三、指数函数的图象和性质
函数 y=ax(a>0,且a≠1)
图象 01
图象特征 在x轴 ,过定点
上方
(0,1)
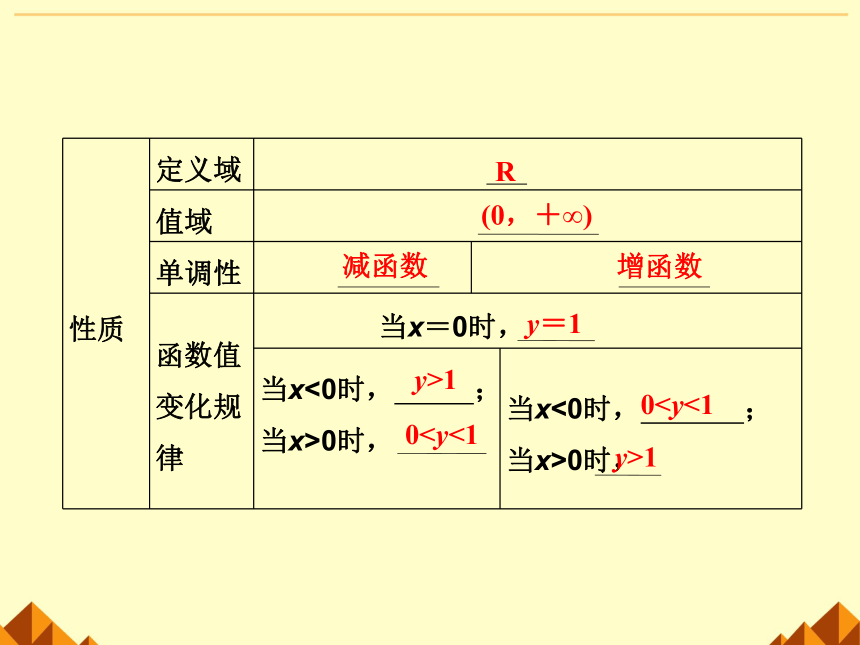
性质 定义域
值域
单调性
函数值变化规律 当x=0时,
当x<0时, ;当x>0时, 当x<0时, ;当x>0时,
(0,+∞)
减函数
增函数
y=1
y>1
00y>1
R
答案:B
2.(2012·湖州模拟)函数y=lg(1-x)的定义域为A,函
数y=3x的值域为B,则A∪B= ( )
A.(0,1) B.(1,3)
C.R D.
解析:A={x|x<1},B={y|y>0},∴A∪B=R.
答案:C
3.已知函数f(x)=4+ax-1的图象恒过定点P,则点P的
坐标是 ( )
A.(1,5) B.(1,4)
C.(0,4) D.(4,0)
解析:当x=1时,f(x)=5.
答案:A
答案: [-1,-∞)
答案:(0,+∞)
1.分数指数幂与根式的关系
分数指数幂与根式可以相互转化,通常利用分数指数幂的意义把根式的运算转化为幂的运算,从而简化计算过程.
2.函数y=ax、y=|ax|、y=a|x|(a>0,a≠1)三者之间的关系
函数y=ax与y=|ax|是同一个函数的不同表现形式,
函数y=a|x|与y=ax不同,前者是一个偶函数,其图象
关于y轴对称,当x≥0时两函数图象相同.
[巧练模拟]——————(课堂突破保分题,分分必保!)
答案:A
[冲关锦囊]
指数幂的化简与求值的原则及结果要求
1.化简原则
(1)化负指数为正指数;
(2)化根式为分数指数幂;
(3)化小数为分数;
(4)注意运算的先后顺序.
2.结果要求
(1)若题目以根式形式给出,则结果用根式表示;
(2)若题目以分数指数幂的形式给出,则结果用分数指
数幂表示;
(3)结果不能同时含有根号和分数指数幂,也不能既有
分母又有负指数幂.
[例2] (2011·萧山一模)函数f(x)=ax-b
的图象如图所示,其中a、b为常数,
则下列结论正确的是 ( )
A.a>1,b<0
B.a>1,b>0
C.00
D.0[自主解答] 由图象得函数是减函数,
∴0又分析得,图象是由y=ax的图象
向左平移所得,
∴-b>0,即b<0.从而D正确.
[答案] D
答案: A
4.(2011·安康二模)方程|3x-1|=k有两解,则k的范围
为________.
解析:函数y=|3x-1|的图象是由
函数y=3x的图象向下平移一个单
位后,再把位于x轴下方的图象沿
x轴翻折到x轴上方得到的,函数
图象如图所示.
∴当0答案: (0,1)
[冲关锦囊]
1.与指数函数有关的函数的图象的研究,往往利用相应
指数函数的图象,通过平移、对称变换得到其图象.
2.一些指数方程、不等式问题的求解,往往利用相应的
指数型函数图象数形结合求解.
[答案] [2,+∞)
若函数变为f(x)=a|2x-4|(a>0,a≠1)且f(1)=9.则f(x)的单调递减区间是________.
解析:由f(1)=9得a2=9,∴a=3.因此f(x)=3|2x-4|,
又∵g(x)=|2x-4|在(-∞,2]内单调递减,∴f(x)的单调递减区间是(-∞,2].
答案:(-∞,2]
[巧练模拟]—————(课堂突破保分题,分分必保!)
5.(2012·温州调研)设函数f(x)=a-|x|(a>0,且a≠1),
f(2)=4,则 ( )
A.f(-2)>f(-1) B.f(-1)>f(-2)
C.f(1)>f(2) D.f(-2)>f(2)
答案: A
6.(2011·长安二模)若函数f(x)=ax-1(a>0,a≠1)的定义
域和值域都是[0,2],则实数a等于________.
[冲关锦囊]
求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归纳为内层函数相关的问题加以解决.
解题样板 指数幂大小的比较方法
答案:A
[高手点拨]
本题给出三种比较指数幂大小的方法,法一是构造函数法,利用指数函数性质比较大小,利用这种方法应注意底数是否大于1;法二与法三两种方法相类似,都是对a、b、c进行简单变形,转化为同次根式的形式,由被开方数的大小可得出a、b、c的大小.
实数指数幂及其运算
函数
、导数及其应用
指数函数
抓 基 础
明 考 向
提 能 力
教 你 一 招
我 来 演 练
[备考方向要明了]
考 什 么
1.了解指数函数模型的实际背景.
2.理解有理数指数幂的含义,了解实数指数幂的意义,
掌握幂的运算.
3.理解指数幂的概念,理解指数函数的单调性,会解决
与指数函数性质有关的问题.
怎 么 考
1.指数函数的概念、图象与性质是近几年高考的热点.
2.通过具体问题考查指数函数的图象与性质,或利用指数函
数的图象与性质解决一些实际问题是重点,也是难点,同
时考查分类讨论思想和数形结合思想.
3.题型以选择题和填空题为主,与其他知识点交汇则以解答
题的形式出现.
一、根式
1.根式的概念
xn=a
正数
负数
两个
相反数
2.两个重要公式
a
-a
a
a
0
没有意义
2.有理数指数幂的性质
(1)aras= (a>0,r,s∈Q);
(2)(ar)s= (a>0,r,s∈Q);
(3)(ab)r= (a>0,b>0,r∈Q).
ar+s
ars
arbr
三、指数函数的图象和性质
函数 y=ax(a>0,且a≠1)
图象 0
图象特征 在x轴 ,过定点
上方
(0,1)
性质 定义域
值域
单调性
函数值变化规律 当x=0时,
当x<0时, ;当x>0时, 当x<0时, ;当x>0时,
(0,+∞)
减函数
增函数
y=1
y>1
0
R
答案:B
2.(2012·湖州模拟)函数y=lg(1-x)的定义域为A,函
数y=3x的值域为B,则A∪B= ( )
A.(0,1) B.(1,3)
C.R D.
解析:A={x|x<1},B={y|y>0},∴A∪B=R.
答案:C
3.已知函数f(x)=4+ax-1的图象恒过定点P,则点P的
坐标是 ( )
A.(1,5) B.(1,4)
C.(0,4) D.(4,0)
解析:当x=1时,f(x)=5.
答案:A
答案: [-1,-∞)
答案:(0,+∞)
1.分数指数幂与根式的关系
分数指数幂与根式可以相互转化,通常利用分数指数幂的意义把根式的运算转化为幂的运算,从而简化计算过程.
2.函数y=ax、y=|ax|、y=a|x|(a>0,a≠1)三者之间的关系
函数y=ax与y=|ax|是同一个函数的不同表现形式,
函数y=a|x|与y=ax不同,前者是一个偶函数,其图象
关于y轴对称,当x≥0时两函数图象相同.
[巧练模拟]——————(课堂突破保分题,分分必保!)
答案:A
[冲关锦囊]
指数幂的化简与求值的原则及结果要求
1.化简原则
(1)化负指数为正指数;
(2)化根式为分数指数幂;
(3)化小数为分数;
(4)注意运算的先后顺序.
2.结果要求
(1)若题目以根式形式给出,则结果用根式表示;
(2)若题目以分数指数幂的形式给出,则结果用分数指
数幂表示;
(3)结果不能同时含有根号和分数指数幂,也不能既有
分母又有负指数幂.
[例2] (2011·萧山一模)函数f(x)=ax-b
的图象如图所示,其中a、b为常数,
则下列结论正确的是 ( )
A.a>1,b<0
B.a>1,b>0
C.0
D.0
∴0
向左平移所得,
∴-b>0,即b<0.从而D正确.
[答案] D
答案: A
4.(2011·安康二模)方程|3x-1|=k有两解,则k的范围
为________.
解析:函数y=|3x-1|的图象是由
函数y=3x的图象向下平移一个单
位后,再把位于x轴下方的图象沿
x轴翻折到x轴上方得到的,函数
图象如图所示.
∴当0
[冲关锦囊]
1.与指数函数有关的函数的图象的研究,往往利用相应
指数函数的图象,通过平移、对称变换得到其图象.
2.一些指数方程、不等式问题的求解,往往利用相应的
指数型函数图象数形结合求解.
[答案] [2,+∞)
若函数变为f(x)=a|2x-4|(a>0,a≠1)且f(1)=9.则f(x)的单调递减区间是________.
解析:由f(1)=9得a2=9,∴a=3.因此f(x)=3|2x-4|,
又∵g(x)=|2x-4|在(-∞,2]内单调递减,∴f(x)的单调递减区间是(-∞,2].
答案:(-∞,2]
[巧练模拟]—————(课堂突破保分题,分分必保!)
5.(2012·温州调研)设函数f(x)=a-|x|(a>0,且a≠1),
f(2)=4,则 ( )
A.f(-2)>f(-1) B.f(-1)>f(-2)
C.f(1)>f(2) D.f(-2)>f(2)
答案: A
6.(2011·长安二模)若函数f(x)=ax-1(a>0,a≠1)的定义
域和值域都是[0,2],则实数a等于________.
[冲关锦囊]
求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归纳为内层函数相关的问题加以解决.
解题样板 指数幂大小的比较方法
答案:A
[高手点拨]
本题给出三种比较指数幂大小的方法,法一是构造函数法,利用指数函数性质比较大小,利用这种方法应注意底数是否大于1;法二与法三两种方法相类似,都是对a、b、c进行简单变形,转化为同次根式的形式,由被开方数的大小可得出a、b、c的大小.
