人教版(B版2019课标)高中数学必修二第四章指数函数、对数函数与幂函数4.1.1实数指数幂及其运算 课件(共27张PPT)
文档属性
| 名称 | 人教版(B版2019课标)高中数学必修二第四章指数函数、对数函数与幂函数4.1.1实数指数幂及其运算 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 382.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
指数与指数函数
基础梳理
1. 根式
(1)定义:如果xn=a,那么x叫做a的________,
其中n>1,n∈N*.当n是奇数时,正数的n次方
根是一个________,负数的n次方根是一个________,
记作________.当n是偶数时,正数的n次方根
有________,这两个数互为________,
记作________,负数没有________方根,
零的n次方根是零.
负数
偶次
n次方根
正数
两个
相反数
(2)两个重要公式
①
② (注意:a必须使有意义)
-a
a
|a|
a
a
2. 有理数指数幂
(1)幂的有关概念
①正分数指数幂: ______
(a>0,m,n∈N*,且n>1);
②负分数指数幂: =________=________.
(a>0,m,n∈N*,且n>1).
③0的正分数指数幂等于______,
0的负分数指数幂___________.
(2)有理数指数幂的性质
①aras=________(a>0,r,s∈Q);
②(ar)s=________(a>0,r,s∈Q);
③(ab)r=________(a>0,b>0,r∈Q).
没有意义
0
arbr
ar+s
ars
3. 指数函数的定义
一般地,函数y=ax(a>0,且a 1)叫做指数函数,
其中x是自变量.
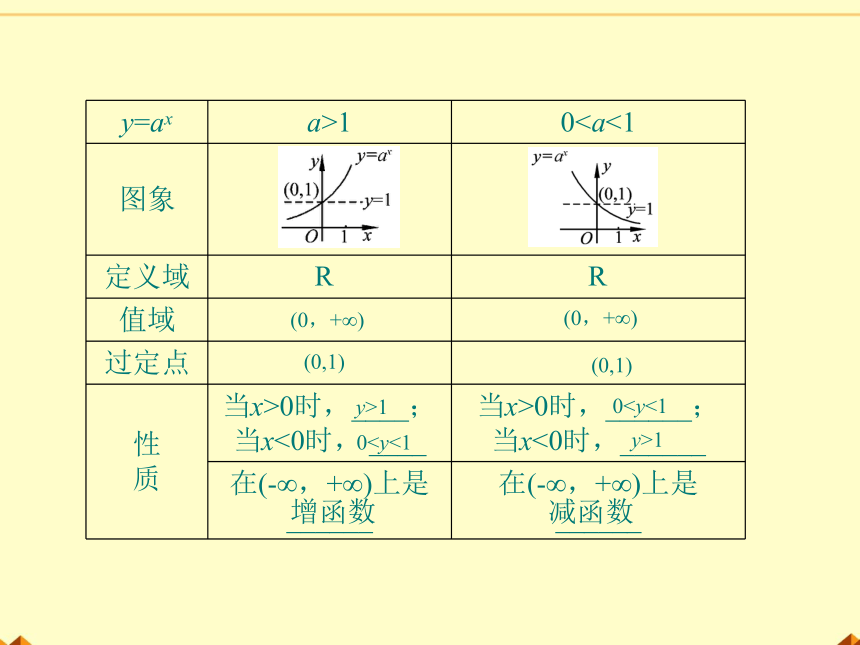
4. 指数函数的图象与性质
y=ax a>1 0图象
定义域
值域
过定点
性 质 当x>0时,____;当x<0时, ____ 当x>0时,______;
当x<0时,______
在(-∞,+∞)上是______ 在(-∞,+∞)上是______
R
R
(0,+∞)
(0,+∞)
(0,1)
(0,1)
y>1
00y>1
增函数
减函数
(教材改编题)化简 (x<0,y<0)得
( )
A. 3x2y B. 3xy C. 9x2y D. -3x2y
基础达标
D 解析:
2. 若函数y=(a2-3a+3)×ax是指数函数,则有
( )
A. a=1或a=2 B. a=1
C. a=2 D. a>0且a≠1
C 解析:
由y=(a2-3a+3)×ax为指数函数,
可得 即a=2.
3. 设指数函数f(x)=ax(a>0且a≠1),
则下列等式不正确的是( )
A. f(x+y)=f(x)×f(y) B. f((xy)n)=fn(x)×fn(y)
C. f(x-y)= D. f(nx)=f n(x)
B 解析:
对于A,f(x+y)=ax+y=ax×ay=f(x)×f(y),所以A正确;
对于B,f((xy)n)=a(xy)n (ax)n(ay)n=fn(x)×fn(y),
所以B不正确;
对于C,f(x-y)=ax-y= ,所以C正确;
对于D,f(nx)=anx=(ax)n=[f(x)]n=fn(x),所以D正确.
4. 已知集合M={-1,1},N= ,
则M∩N=________.
{-1} 解析:
<2x+1<4 即为2-1<2x+1<22,因为y=2x在R上
是增函数,所以-1所以x=-1,0,
所以N={-1,0},因此M∩N={-1}.
5. (教材改编题)函数 的定义域为
________,值域为________.
{x|x≠0} {y|y>0且y≠1}
解析:
定义域为{x|x≠0},∵ ∴
∴值域为{y|y>0且y ≠ 1}.
【例1】 化简或计算.
(1)
(2)已知a,b是方程x2-6x+4=0的两根,且a>b>0,
求 的值.
经典例题
题型一 指数运算性质的应用
分析:
有理指数幂的运算应注意“化小数为分数”、“化根式为分数指数幂”的原则.
(2)由条件知a+b=6,ab=4,又a>b>0,所以
【例2】 已知函数
(1)作出函数的图象;
(2)指出该函数的单调递增区间;
(3)求函数的值域.
题型二 指数函数的图象的应用
分析:本题要考虑去绝对值符号,把函数解
析式写成分段函数的形式,再作出图象,然
后根据图象寻求其单调递增区间和值域.
解:(1)由函数解析式可得
其图象分成两部分:一部分是
的图象,由下列变换可得到:
另一部分y=2x+2(x<-2)的图象,
由下列变换可得到:
左移2个单位
左移2个单位
函数 的图象如图
(2)由图象观察知函数在(-∞,-2]上是增函数.
(3)由图象观察知,x=-2时,函数
有最大值,最大值为1,没有最小值,
故其值域为(0,1].
若函数y=ax+b-1(a>0,且a≠1)的图象经过
第二、三、四象限,则一定有( )
A. 0<a<1,且b>0 B. a>1,且b>0
C. 0<a<1,且b<0 D. a>1,且b<0
变式2-1
如图,图象与y轴的交点在y轴的负半轴上
(纵截距小于零),即a0+b-1<0,且0<a<1,
∴0<a<1,且b<0.故选C.
C 解析:
【例3】 求下列函数的定义域和值域.
(1) (2)
.
题型三 指数函数性质的应用
分析:指数函数y=ax(a>0,且a≠1)的定义域为R,所以y=af(x)的定义域与f(x)定义域相同;值域则要应用其单调性来求,复合函数则要注意“同增异减”的原则.
解:(1)因为2x+1>0恒成立,所以定义域为R.
又因为 ,而
所以 ,解得0.
(2)令-x2-3x+4≥0,解得-4≤x≤1,所以函数
的定义域为[-4,1].设 (-4≤x≤1),
易得u在 时取最大值
在x=-4或1时取最小值0,即0≤u≤
所以函数y=2u的值域为
即函数 的值域为
下列函数中值域为正实数集的是( )
A. B.
C. D.
变式3-1
A 解析:
A中 的值域为正实数集,而1-x∈R,
∴ 的值域为正实数集;
B中,当x=0时,2x-1=0;
C中,y取不到1;D中,函数值域为[0,1).
【例4】 已知定义在R上的奇函数f(x)有最小
正周期2,且当x∈(0,1)时,
求f(x)在[-1,1]上的解析式.
题型四 指数函数性质的综合应用
分析:
求f(x)在[-1,1]上的解析式,可以先求f(x)在(-1,0)上
的解析式.
解:当x∈(-1,0)时,-x∈(0,1).∵f(x)是奇函数,
∴
由f(0)=-f(0),且f(1)=f(-2+1)=f(-1)=-f(1),
得f(0)=f(1)=f(-1)=0. ∴在区间[-1,1]上,有
易错警示
【例】设a>0且a≠1,如果函数f(x)=a2x+2ax-1
在[-1,1]上的最大值为14,求a的值.
错解
当x=1时,f(x)有最大值,即a2+2a-1=14,
∴a2+2a-15=0,∴a=3(a=-5舍去).
错解分析
错解中:(1)忽略了字母参数a>1与0同情况,默认f(x)在[-1,1]上单调递增;
(2)对于f(x)=a2x+2ax-1=(ax+1)2-2,没有从ax本身
的范围与f(x)单调性之间关系去考虑问题.
y=(ax+1)2-2,x∈[-1,1].
(1)当a>1时,ax∈ ,令t=ax,
则y=(t+1)2-2,t∈ ,
易知y=(t+1)2-2在 上单调递增.
∴当t=a,即ax=a时,ymax=(a+1)2-2=14,
∴a=3(a=-5舍去).
(2)当0同(1)得当t= ,
即ax= 时,ymax= -2=14,
解得a= .
综上所述,a= 或a=3.
指数与指数函数
基础梳理
1. 根式
(1)定义:如果xn=a,那么x叫做a的________,
其中n>1,n∈N*.当n是奇数时,正数的n次方
根是一个________,负数的n次方根是一个________,
记作________.当n是偶数时,正数的n次方根
有________,这两个数互为________,
记作________,负数没有________方根,
零的n次方根是零.
负数
偶次
n次方根
正数
两个
相反数
(2)两个重要公式
①
② (注意:a必须使有意义)
-a
a
|a|
a
a
2. 有理数指数幂
(1)幂的有关概念
①正分数指数幂: ______
(a>0,m,n∈N*,且n>1);
②负分数指数幂: =________=________.
(a>0,m,n∈N*,且n>1).
③0的正分数指数幂等于______,
0的负分数指数幂___________.
(2)有理数指数幂的性质
①aras=________(a>0,r,s∈Q);
②(ar)s=________(a>0,r,s∈Q);
③(ab)r=________(a>0,b>0,r∈Q).
没有意义
0
arbr
ar+s
ars
3. 指数函数的定义
一般地,函数y=ax(a>0,且a 1)叫做指数函数,
其中x是自变量.
4. 指数函数的图象与性质
y=ax a>1 0
定义域
值域
过定点
性 质 当x>0时,____;当x<0时, ____ 当x>0时,______;
当x<0时,______
在(-∞,+∞)上是______ 在(-∞,+∞)上是______
R
R
(0,+∞)
(0,+∞)
(0,1)
(0,1)
y>1
0
增函数
减函数
(教材改编题)化简 (x<0,y<0)得
( )
A. 3x2y B. 3xy C. 9x2y D. -3x2y
基础达标
D 解析:
2. 若函数y=(a2-3a+3)×ax是指数函数,则有
( )
A. a=1或a=2 B. a=1
C. a=2 D. a>0且a≠1
C 解析:
由y=(a2-3a+3)×ax为指数函数,
可得 即a=2.
3. 设指数函数f(x)=ax(a>0且a≠1),
则下列等式不正确的是( )
A. f(x+y)=f(x)×f(y) B. f((xy)n)=fn(x)×fn(y)
C. f(x-y)= D. f(nx)=f n(x)
B 解析:
对于A,f(x+y)=ax+y=ax×ay=f(x)×f(y),所以A正确;
对于B,f((xy)n)=a(xy)n (ax)n(ay)n=fn(x)×fn(y),
所以B不正确;
对于C,f(x-y)=ax-y= ,所以C正确;
对于D,f(nx)=anx=(ax)n=[f(x)]n=fn(x),所以D正确.
4. 已知集合M={-1,1},N= ,
则M∩N=________.
{-1} 解析:
<2x+1<4 即为2-1<2x+1<22,因为y=2x在R上
是增函数,所以-1
所以N={-1,0},因此M∩N={-1}.
5. (教材改编题)函数 的定义域为
________,值域为________.
{x|x≠0} {y|y>0且y≠1}
解析:
定义域为{x|x≠0},∵ ∴
∴值域为{y|y>0且y ≠ 1}.
【例1】 化简或计算.
(1)
(2)已知a,b是方程x2-6x+4=0的两根,且a>b>0,
求 的值.
经典例题
题型一 指数运算性质的应用
分析:
有理指数幂的运算应注意“化小数为分数”、“化根式为分数指数幂”的原则.
(2)由条件知a+b=6,ab=4,又a>b>0,所以
【例2】 已知函数
(1)作出函数的图象;
(2)指出该函数的单调递增区间;
(3)求函数的值域.
题型二 指数函数的图象的应用
分析:本题要考虑去绝对值符号,把函数解
析式写成分段函数的形式,再作出图象,然
后根据图象寻求其单调递增区间和值域.
解:(1)由函数解析式可得
其图象分成两部分:一部分是
的图象,由下列变换可得到:
另一部分y=2x+2(x<-2)的图象,
由下列变换可得到:
左移2个单位
左移2个单位
函数 的图象如图
(2)由图象观察知函数在(-∞,-2]上是增函数.
(3)由图象观察知,x=-2时,函数
有最大值,最大值为1,没有最小值,
故其值域为(0,1].
若函数y=ax+b-1(a>0,且a≠1)的图象经过
第二、三、四象限,则一定有( )
A. 0<a<1,且b>0 B. a>1,且b>0
C. 0<a<1,且b<0 D. a>1,且b<0
变式2-1
如图,图象与y轴的交点在y轴的负半轴上
(纵截距小于零),即a0+b-1<0,且0<a<1,
∴0<a<1,且b<0.故选C.
C 解析:
【例3】 求下列函数的定义域和值域.
(1) (2)
.
题型三 指数函数性质的应用
分析:指数函数y=ax(a>0,且a≠1)的定义域为R,所以y=af(x)的定义域与f(x)定义域相同;值域则要应用其单调性来求,复合函数则要注意“同增异减”的原则.
解:(1)因为2x+1>0恒成立,所以定义域为R.
又因为 ,而
所以 ,解得0
(2)令-x2-3x+4≥0,解得-4≤x≤1,所以函数
的定义域为[-4,1].设 (-4≤x≤1),
易得u在 时取最大值
在x=-4或1时取最小值0,即0≤u≤
所以函数y=2u的值域为
即函数 的值域为
下列函数中值域为正实数集的是( )
A. B.
C. D.
变式3-1
A 解析:
A中 的值域为正实数集,而1-x∈R,
∴ 的值域为正实数集;
B中,当x=0时,2x-1=0;
C中,y取不到1;D中,函数值域为[0,1).
【例4】 已知定义在R上的奇函数f(x)有最小
正周期2,且当x∈(0,1)时,
求f(x)在[-1,1]上的解析式.
题型四 指数函数性质的综合应用
分析:
求f(x)在[-1,1]上的解析式,可以先求f(x)在(-1,0)上
的解析式.
解:当x∈(-1,0)时,-x∈(0,1).∵f(x)是奇函数,
∴
由f(0)=-f(0),且f(1)=f(-2+1)=f(-1)=-f(1),
得f(0)=f(1)=f(-1)=0. ∴在区间[-1,1]上,有
易错警示
【例】设a>0且a≠1,如果函数f(x)=a2x+2ax-1
在[-1,1]上的最大值为14,求a的值.
错解
当x=1时,f(x)有最大值,即a2+2a-1=14,
∴a2+2a-15=0,∴a=3(a=-5舍去).
错解分析
错解中:(1)忽略了字母参数a>1与0
(2)对于f(x)=a2x+2ax-1=(ax+1)2-2,没有从ax本身
的范围与f(x)单调性之间关系去考虑问题.
y=(ax+1)2-2,x∈[-1,1].
(1)当a>1时,ax∈ ,令t=ax,
则y=(t+1)2-2,t∈ ,
易知y=(t+1)2-2在 上单调递增.
∴当t=a,即ax=a时,ymax=(a+1)2-2=14,
∴a=3(a=-5舍去).
(2)当0
即ax= 时,ymax= -2=14,
解得a= .
综上所述,a= 或a=3.
