粤教版(2019)高中信息技术 3.2算法及算法描述 课件(27PPT)
文档属性
| 名称 | 粤教版(2019)高中信息技术 3.2算法及算法描述 课件(27PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
3.2 算法及算法描述
第三章 算法基础
课题引入
找两个数的
最大公约数比赛
知道他为什么计算这么快吗?
.给定两个正整数m=112,n=64,求最大公约数。
某同学方法如下:
比一比
Step1.112除以64,余数为___
Step2.____除以____,余数为___
Step3.____除以____,余数为___
答:112和64的最大公约数为___
48
64
48
16
48
16
0
16
巧用计算机解决问题提高效率
第三章 算法基础
3.2算法及其描述
第三章 算法基础
3.2算法及其描述
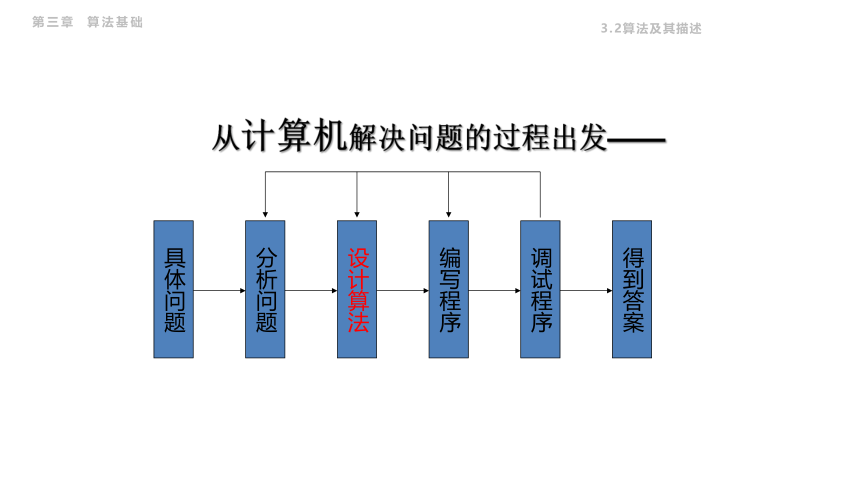
从计算机解决问题的过程出发——
具体问题
分析问题
设计算法
编写程序
调试程序
得到答案
3.2.1
什么是算法
观看素材空间提供的学习视频素材,结合教材“3.2.1算法”,算法的定义 “、”算法的特征“。
概述算法的概念和特征
项目实施
Step1.r=m mod n
Step2.若r=0,则输出结果n,算法结束;
否则,继续step3
Step3.令m=n,n=r,返回step1
几何学的鼻祖,古希腊数学家欧几里得创立了著名的欧几里得几何,简称欧氏几何。其中阐述了关于求两个整数的最大公约数的过程,叫辗转相除法,就是古人留下来的一种算法。
算法是指在有限步骤内求解某一问题所使用的一组定义明确的规则。通俗地说,算法就是用计算机求解某一问题的方法,是能被机械地执行的动作或指令的有穷集合。
算法是程序设计的灵魂:
算法+数据结构(Data Structure)=程序。
算法独立于任何具体的程序设计语言,一个算法可以用多种语言来实现。
你知道世界上最早的算法?
巴比伦人发明的六十进制,我们现在关于时分秒和角度的记法就是从他们那里学来的。
3.2.1
什么是算法
1.输入:一个算法有0个或多个输入,以刻画运算对象的初始情况。2.确定性:算法的每一步骤必须有确切的定义;3.有穷性:一个算法必须执行有限步骤之后结束。4.输出:算法至少有1个输出,即最终结果。没有输出的算法是毫无意义的。5.可行性:算法原则上能够精确地运行,而且人们用笔和纸做有限次运算后即可完成。3.2.1算法的特征 开学之际,同学们纷纷忙于购置各种学习文具,假设现在同学手中有50元的现金,用于购买下列物品,以何种方式搭配购买能够让资金最大化利用呢?
笔记本
单价:6元/本
签字笔
单价:5元/支
橡皮
单价:4元/块
讨
论
买文具问题转化为求解方程:6x+5y+4z=50的正整数解个数t。
探究活动
第三章 算法基础
分
析
3.2算法及其描述
分析问题:x的取值范围1~8本,y的取值范围1~10支,z的取值范围1~12块,那么x,y,z的取值组合有几种?
利用穷举法的思想,对每一种x、y、z的取值组合进行计算,如果正好等于50就输出x、y、z的值,t自增1并输出。
然后判断下一个取值组合,直到判断完所有的组合。
买文具问题转化为求解方程:6x+5y+4z=50的正整数解。
探究活动
第三章 算法基础
分
析
3.2算法及其描述
解决方法如下:
t=0;
x=1;
y=1;
z=1;
如果6x+5y+4z=50,则解的个数加1,输出这个解;
z=z+1;
如果z<=12则转到⑤,否则继续⑧;
y=y+1;
如果y<=10则转到④,否则继续⑩;
x=x+1;
如果x<=8则转到③,否则继续12;
结束。
买文具问题转化为求解方程:6x+5y+4z=50的正整数解的python程序如下:
探究活动
实现
现
t=0
for x in range(1,9):
for y in range(1,11):
for z in range(1,13):
if x*6+y*5+z*4==50:
print(x,y,z)
t=t+1
print("解的个数",t)
编写程序
第三章 算法基础
3.1体验计算机解决问题的过程
调试运行
体
验
请根据老师的演示,尝试打开电脑上的“解三元一次方程.py”代码文件,并运行程序,观察程序运行结果,得出结论。
买笔记本问题转化为求解方程:6x+5y+4z=50的正整数解
探究活动
第三章 算法基础
实
现
方案 x y z 合计
1 1 4 6 11
2 1 8 1 10
3 2 2 7 11
4 2 6 2 10
5 3 4 3 10
6 4 2 4 10
7 6 2 1 9
3.2算法及其描述
1.用自然语言描述算法
用自然语言描述算法,就是用人们日常所用的语言,如:汉语、英语等来描述算法。
第三章 算法基础
3.2.2
算法的描述
t=0;
x=1;
y=1;
z=1;
如果满足式子6x+5y+4z=50,则购买的方案数加1(即t=t+1),并输出这种购买方案(即输出t、x、y、z的值)。
z=z+1;
如果z<=12则转⑤,否则继续⑧;
y=y+1;
如果y<=10则转④,否则继续⑩;
x=x+1;
如果x<=8则转③,否则继续 ;
结束。
3.2算法及其描述
2.用流程图描述算法
用ANSI制定的一系列流程图符号来描述算法的一种表示方法。使用流程图描述算法,让人感到算法的形象直观简洁。流程图的基本图形及其功能如下表所示。(例:教材图3-8)
第三章 算法基础
图 形 名 称 功 能
开始/结束 开始或结束
输入/输出 输入或输出
处理 计算与赋值
判断 条件判断
流程线 表示算法中的流向
连接点 表示算法中的转接
表3-4流程图的基本图形及其功能表所示。
3.2.2
算法的描述
3.2算法及其描述
探究活动
这三种基本控制结构的主要作用是:
(1)顺序结构表示程序中的各操作是按照它们出现的先后顺序执行的。
(2)选择结构表示程序的处理步骤出现了分支,它需要根据某一特定的条件选择其中的一个分支执行。选择结构有单选择、双选择和多选择三种形式。
(3)循环结构表示程序反复执行某个或某些操作,直到某条件为假时才可终止循环,结构中有返回跳转。
讨
论
观看光盘视频掌握算法的三种基本控制结构
第三章 算法基础
3.2算法及其描述
3.用流程图描述购买文具问题的算法
第三章 算法基础
3.2.2
算法的描述
3.2算法及其描述
3.用伪代码描述算法
用伪代码描述算法就是用介于自然语言和计算机语言之间的文字和符号来描述算法。
第三章 算法基础
t=0
for x in range(1,9):
for y in range(1,11):
for z in range(1,13):
if x*6+y*5+z*4==50:
{t=t+1;
输出解的个数t和三个整数x,y,z}
3.2.2
算法的描述
3.2算法及其描述
分组讨论:
辗转相除法的三种算法描述。
设给定的两个正整数为m和n,求它们的最大公约数的步骤为:
以m除以n,令所得余数为r。
若r=0,则输出结果n,算法结束;否则继续③。
令m=n,n=r,并返回①继续。
项目实施
第三章 算法基础
3.2算法及其描述
探究活动
实
践
辗转相除法的算法描述展评
第三章 算法基础
自然语言表示法 流程图表示法 伪代码表示法
示例 ①输入两个正整数m,n(m>n); ②计算m除以n所得的余数r; ③m=n,n=r; ④若r=0,则m,n的最大公约数等于m;否则转到步骤②; ⑤输出最大公约数m; ⑥结束。 m=input("m=")
n=input("n=")
if m < n:
t=m, m = n, n=t
r = m% n
while r != 0:
r = m% n
m = n
n = r
print m
3.2算法及其描述
探究活动
讨
论
算法三种描述方法的优劣对比
第三章 算法基础
算法描述的方法 优势 不足
自然语言表示法 用人们日常所用的语言,比较容易掌握。 当算法中含有多分支或循环操作较多时很难清晰地表示出来,由于自然语言的歧义性,容易导致算法执行的不确定性。
流程图表示法 用程序框图来描述,流程描述清晰简洁。 所占篇幅较大,由于允许使用流程线,过于灵活,不受约束。
伪代码表示法 用介于自然语言和计算机语言之间的文字和符号来描述,书写方便,格式紧凑,易于理解,便于向计算机程序设计语言过渡。 由于编程语言的种类繁多,伪代码的语句不容易规范,有时会产生误解。
3.2算法及其描述
算法是程序设计的核心,是程序设计的灵魂。算法的好坏,直接影响着程序的通用性和有效性,影响着问题解决的效率,算法不唯一,同一个算法可以用多种程序设计语言来实现。恰当的算法描述更有利于编写程序。
要点:算法描述要完整,步骤要清晰,符合算法的特征,有效解决项目的关键问题。
第三章 算法基础
3.2算法及其描述
课堂小结
1、用计算机解决某个问题,问题分析清楚后,给出解决这个问题的( ),这个过程称为设计算法。
A、编程语言B、程序代码 C、方法和步骤 D、加密措施
2、用流程图表示条件“A>B”是否成立,要用到以下哪个图形?( )
A 平行四边形 B 菱形 C 圆角矩形 D直角矩形
3、 用自然语言描述一下解决以下问题的算法:借助一个空杯将一杯橙汁和一杯可乐互换所盛放的杯子。
课堂练习
过程步骤第三章 算法基础3.1体验计算机解决问题的过程[参考答案](1)橙汁倒入空杯;(2)可乐倒入刚空出的杯子;(3)橙汁倒入刚倒出可乐的杯子第三章 算法基础
设计一个算法,输入半径r,输出圆的面积S和周长L。
设计一个算法,求鸡兔同笼问题:上有头a个,下有脚b只,问鸡兔各几何?
设计一个算法,求两个数中的最大数。
设计一个算法,求实数a的绝对值。
课后作业
3.2算法及其描述
3.2 算法及算法描述
第三章 算法基础
课题引入
找两个数的
最大公约数比赛
知道他为什么计算这么快吗?
.给定两个正整数m=112,n=64,求最大公约数。
某同学方法如下:
比一比
Step1.112除以64,余数为___
Step2.____除以____,余数为___
Step3.____除以____,余数为___
答:112和64的最大公约数为___
48
64
48
16
48
16
0
16
巧用计算机解决问题提高效率
第三章 算法基础
3.2算法及其描述
第三章 算法基础
3.2算法及其描述
从计算机解决问题的过程出发——
具体问题
分析问题
设计算法
编写程序
调试程序
得到答案
3.2.1
什么是算法
观看素材空间提供的学习视频素材,结合教材“3.2.1算法”,算法的定义 “、”算法的特征“。
概述算法的概念和特征
项目实施
Step1.r=m mod n
Step2.若r=0,则输出结果n,算法结束;
否则,继续step3
Step3.令m=n,n=r,返回step1
几何学的鼻祖,古希腊数学家欧几里得创立了著名的欧几里得几何,简称欧氏几何。其中阐述了关于求两个整数的最大公约数的过程,叫辗转相除法,就是古人留下来的一种算法。
算法是指在有限步骤内求解某一问题所使用的一组定义明确的规则。通俗地说,算法就是用计算机求解某一问题的方法,是能被机械地执行的动作或指令的有穷集合。
算法是程序设计的灵魂:
算法+数据结构(Data Structure)=程序。
算法独立于任何具体的程序设计语言,一个算法可以用多种语言来实现。
你知道世界上最早的算法?
巴比伦人发明的六十进制,我们现在关于时分秒和角度的记法就是从他们那里学来的。
3.2.1
什么是算法
1.输入:一个算法有0个或多个输入,以刻画运算对象的初始情况。2.确定性:算法的每一步骤必须有确切的定义;3.有穷性:一个算法必须执行有限步骤之后结束。4.输出:算法至少有1个输出,即最终结果。没有输出的算法是毫无意义的。5.可行性:算法原则上能够精确地运行,而且人们用笔和纸做有限次运算后即可完成。3.2.1算法的特征 开学之际,同学们纷纷忙于购置各种学习文具,假设现在同学手中有50元的现金,用于购买下列物品,以何种方式搭配购买能够让资金最大化利用呢?
笔记本
单价:6元/本
签字笔
单价:5元/支
橡皮
单价:4元/块
讨
论
买文具问题转化为求解方程:6x+5y+4z=50的正整数解个数t。
探究活动
第三章 算法基础
分
析
3.2算法及其描述
分析问题:x的取值范围1~8本,y的取值范围1~10支,z的取值范围1~12块,那么x,y,z的取值组合有几种?
利用穷举法的思想,对每一种x、y、z的取值组合进行计算,如果正好等于50就输出x、y、z的值,t自增1并输出。
然后判断下一个取值组合,直到判断完所有的组合。
买文具问题转化为求解方程:6x+5y+4z=50的正整数解。
探究活动
第三章 算法基础
分
析
3.2算法及其描述
解决方法如下:
t=0;
x=1;
y=1;
z=1;
如果6x+5y+4z=50,则解的个数加1,输出这个解;
z=z+1;
如果z<=12则转到⑤,否则继续⑧;
y=y+1;
如果y<=10则转到④,否则继续⑩;
x=x+1;
如果x<=8则转到③,否则继续12;
结束。
买文具问题转化为求解方程:6x+5y+4z=50的正整数解的python程序如下:
探究活动
实现
现
t=0
for x in range(1,9):
for y in range(1,11):
for z in range(1,13):
if x*6+y*5+z*4==50:
print(x,y,z)
t=t+1
print("解的个数",t)
编写程序
第三章 算法基础
3.1体验计算机解决问题的过程
调试运行
体
验
请根据老师的演示,尝试打开电脑上的“解三元一次方程.py”代码文件,并运行程序,观察程序运行结果,得出结论。
买笔记本问题转化为求解方程:6x+5y+4z=50的正整数解
探究活动
第三章 算法基础
实
现
方案 x y z 合计
1 1 4 6 11
2 1 8 1 10
3 2 2 7 11
4 2 6 2 10
5 3 4 3 10
6 4 2 4 10
7 6 2 1 9
3.2算法及其描述
1.用自然语言描述算法
用自然语言描述算法,就是用人们日常所用的语言,如:汉语、英语等来描述算法。
第三章 算法基础
3.2.2
算法的描述
t=0;
x=1;
y=1;
z=1;
如果满足式子6x+5y+4z=50,则购买的方案数加1(即t=t+1),并输出这种购买方案(即输出t、x、y、z的值)。
z=z+1;
如果z<=12则转⑤,否则继续⑧;
y=y+1;
如果y<=10则转④,否则继续⑩;
x=x+1;
如果x<=8则转③,否则继续 ;
结束。
3.2算法及其描述
2.用流程图描述算法
用ANSI制定的一系列流程图符号来描述算法的一种表示方法。使用流程图描述算法,让人感到算法的形象直观简洁。流程图的基本图形及其功能如下表所示。(例:教材图3-8)
第三章 算法基础
图 形 名 称 功 能
开始/结束 开始或结束
输入/输出 输入或输出
处理 计算与赋值
判断 条件判断
流程线 表示算法中的流向
连接点 表示算法中的转接
表3-4流程图的基本图形及其功能表所示。
3.2.2
算法的描述
3.2算法及其描述
探究活动
这三种基本控制结构的主要作用是:
(1)顺序结构表示程序中的各操作是按照它们出现的先后顺序执行的。
(2)选择结构表示程序的处理步骤出现了分支,它需要根据某一特定的条件选择其中的一个分支执行。选择结构有单选择、双选择和多选择三种形式。
(3)循环结构表示程序反复执行某个或某些操作,直到某条件为假时才可终止循环,结构中有返回跳转。
讨
论
观看光盘视频掌握算法的三种基本控制结构
第三章 算法基础
3.2算法及其描述
3.用流程图描述购买文具问题的算法
第三章 算法基础
3.2.2
算法的描述
3.2算法及其描述
3.用伪代码描述算法
用伪代码描述算法就是用介于自然语言和计算机语言之间的文字和符号来描述算法。
第三章 算法基础
t=0
for x in range(1,9):
for y in range(1,11):
for z in range(1,13):
if x*6+y*5+z*4==50:
{t=t+1;
输出解的个数t和三个整数x,y,z}
3.2.2
算法的描述
3.2算法及其描述
分组讨论:
辗转相除法的三种算法描述。
设给定的两个正整数为m和n,求它们的最大公约数的步骤为:
以m除以n,令所得余数为r。
若r=0,则输出结果n,算法结束;否则继续③。
令m=n,n=r,并返回①继续。
项目实施
第三章 算法基础
3.2算法及其描述
探究活动
实
践
辗转相除法的算法描述展评
第三章 算法基础
自然语言表示法 流程图表示法 伪代码表示法
示例 ①输入两个正整数m,n(m>n); ②计算m除以n所得的余数r; ③m=n,n=r; ④若r=0,则m,n的最大公约数等于m;否则转到步骤②; ⑤输出最大公约数m; ⑥结束。 m=input("m=")
n=input("n=")
if m < n:
t=m, m = n, n=t
r = m% n
while r != 0:
r = m% n
m = n
n = r
print m
3.2算法及其描述
探究活动
讨
论
算法三种描述方法的优劣对比
第三章 算法基础
算法描述的方法 优势 不足
自然语言表示法 用人们日常所用的语言,比较容易掌握。 当算法中含有多分支或循环操作较多时很难清晰地表示出来,由于自然语言的歧义性,容易导致算法执行的不确定性。
流程图表示法 用程序框图来描述,流程描述清晰简洁。 所占篇幅较大,由于允许使用流程线,过于灵活,不受约束。
伪代码表示法 用介于自然语言和计算机语言之间的文字和符号来描述,书写方便,格式紧凑,易于理解,便于向计算机程序设计语言过渡。 由于编程语言的种类繁多,伪代码的语句不容易规范,有时会产生误解。
3.2算法及其描述
算法是程序设计的核心,是程序设计的灵魂。算法的好坏,直接影响着程序的通用性和有效性,影响着问题解决的效率,算法不唯一,同一个算法可以用多种程序设计语言来实现。恰当的算法描述更有利于编写程序。
要点:算法描述要完整,步骤要清晰,符合算法的特征,有效解决项目的关键问题。
第三章 算法基础
3.2算法及其描述
课堂小结
1、用计算机解决某个问题,问题分析清楚后,给出解决这个问题的( ),这个过程称为设计算法。
A、编程语言B、程序代码 C、方法和步骤 D、加密措施
2、用流程图表示条件“A>B”是否成立,要用到以下哪个图形?( )
A 平行四边形 B 菱形 C 圆角矩形 D直角矩形
3、 用自然语言描述一下解决以下问题的算法:借助一个空杯将一杯橙汁和一杯可乐互换所盛放的杯子。
课堂练习
过程步骤第三章 算法基础3.1体验计算机解决问题的过程[参考答案](1)橙汁倒入空杯;(2)可乐倒入刚空出的杯子;(3)橙汁倒入刚倒出可乐的杯子第三章 算法基础
设计一个算法,输入半径r,输出圆的面积S和周长L。
设计一个算法,求鸡兔同笼问题:上有头a个,下有脚b只,问鸡兔各几何?
设计一个算法,求两个数中的最大数。
设计一个算法,求实数a的绝对值。
课后作业
3.2算法及其描述
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
