4.1.2指数函数的性质与图像 课件(共19张PPT)
文档属性
| 名称 | 4.1.2指数函数的性质与图像 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 351.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 10:33:42 | ||
图片预览






文档简介
(共19张PPT)
指数函数及其性质
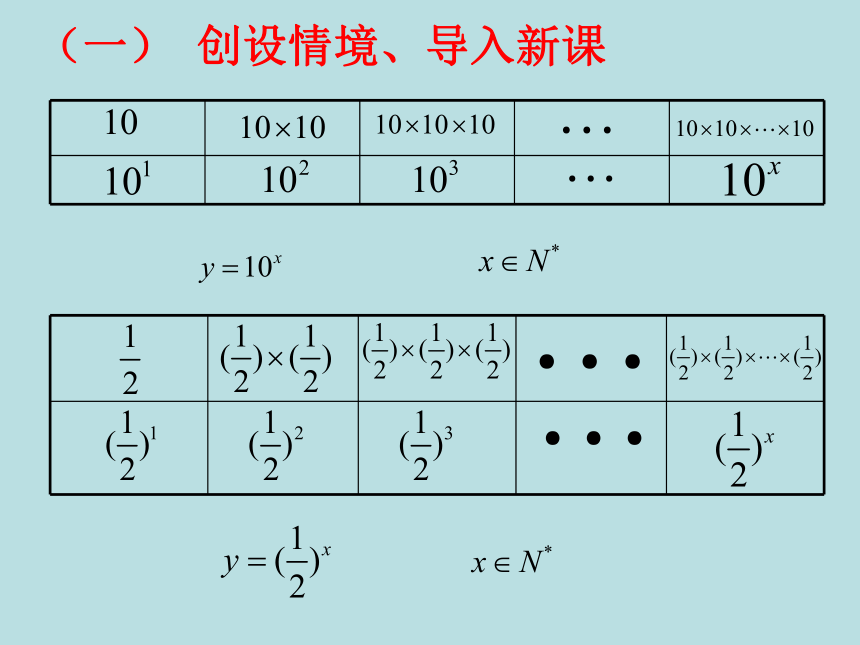
(一) 创设情境、导入新课
上述两个函数有什么样的共同特征?
(1)都是幂的形式;
(2)幂的底数都是一个正常数;
(3)幂的指数都是一个变量。
对应关系 定义域
底为常数
指数为自变量
一般地、函数
叫做指数函数,其中x为自变量,a是常数,定义域为R。
1. 指数函数的概念:
(二) 师生互动、探究新知
探究:定义中为什么要规定
?
探讨: 若不满足上述条件 会怎么样呢
(1)若a=0,则 当x>0时, .
当x≤0时, 无意义.
(2)若a<0,则对于x的某些数值,可使 无意义。
如 ,这时对于 ……,在实数范围内函数值不存在.
以上三种情况都不利于我们研究指数函数,所以规定: a>0 且a≠1.
(3)若a=1,则对于任何 , 是一个
常量,没有研究的必要性.
1
=
x
a
随堂练习:下列函数中,哪些是指数函数?
我是
我还不是
我不是
我也不是
动动手: 请同学们画一画下面两个函数的图像。
8
4
2
1
3
2
1
0
-1
-2
-3
x
-3 -2 -1 0 1 2 3 x
87654321
y
y = 2 x
(3,8)
(2,4)
(1,2)
( 0,1)
(-1, )
(-2, )
(-3, )
-3 -2 -1 0 1 2 3 x
87654321
y
y = ( ) x
3
2
1
0
-1
-2
-3
x
1
2
4
8
-3 -2 -1 0 1 2 3 x
87654321
y
y = 2 x
y = ( ) x
(3,8)
(2,4)
(1,2)
( 0,1)
(-1, )
(-2, )
(-3, )
思考:函数 的图像与 的图像有什么关系 ?可否
利用 的图像画出 的图像 ?
(-3,8)
(-2,4)
(-1,2)
( 0,1)
(2, )
(1, )
(3, )
函数y=2x的图像与 的图像关于y轴对称.
y = ( ) x
x
y
0
y = ( ) x
y = ( ) x
y = 2 x
y = 3 x
思考2:如图四个指数函数图像,当底数大于0小于1和大于1时,图像在画法上有什么特点?
思考3: 通过图像,你能发现指数函数的哪些共同特征?
当底数大于0小于1时,图像自左向右是下降的;
当底数大于1时,图像自左向右是上升的。
1.图像向左、向右是无限延伸的。
2.图像都在x轴的上方。
3.都过定点(0,1)。
(0,1)
2.指数函数 的图像及性质
01
图像
定义域
值域
性 定点
质 单调性
y
x
0
y=1
(0,1)
y
x
0
y=1
(0,1)
(0,+∞)
R
R
(0,+∞)
(0,1) 即 x = 0 时, y = 1 。
在R上是单调增函数
在R上是单调减函数
三、 典例分析
1、已知指数函数
解:因为
所以
故
所以
四、 自作自受
例2.求下列函数的定义域
(1)解:因为
所以
故定义域为:
(2)解:因为
所以
故定义域为:
练2、求下列函数的定义域
四、归纳小结
(1) 通过本节课的学习,你学到了哪些知识?
(2) 你学会了哪些数学思想方法?
1.指数函数的定义以及指数函数的一般表达式的特征;
2.指数函数的图像及其简图的画法;
3.指数函数的性质.
1.数形结合思想;
2.分类讨论思想;
3.从具体到一般的抽象概括的方法。
五、布置作业
课本P58 2 3 P59 5 6
谢谢大家
指数函数及其性质
(一) 创设情境、导入新课
上述两个函数有什么样的共同特征?
(1)都是幂的形式;
(2)幂的底数都是一个正常数;
(3)幂的指数都是一个变量。
对应关系 定义域
底为常数
指数为自变量
一般地、函数
叫做指数函数,其中x为自变量,a是常数,定义域为R。
1. 指数函数的概念:
(二) 师生互动、探究新知
探究:定义中为什么要规定
?
探讨: 若不满足上述条件 会怎么样呢
(1)若a=0,则 当x>0时, .
当x≤0时, 无意义.
(2)若a<0,则对于x的某些数值,可使 无意义。
如 ,这时对于 ……,在实数范围内函数值不存在.
以上三种情况都不利于我们研究指数函数,所以规定: a>0 且a≠1.
(3)若a=1,则对于任何 , 是一个
常量,没有研究的必要性.
1
=
x
a
随堂练习:下列函数中,哪些是指数函数?
我是
我还不是
我不是
我也不是
动动手: 请同学们画一画下面两个函数的图像。
8
4
2
1
3
2
1
0
-1
-2
-3
x
-3 -2 -1 0 1 2 3 x
87654321
y
y = 2 x
(3,8)
(2,4)
(1,2)
( 0,1)
(-1, )
(-2, )
(-3, )
-3 -2 -1 0 1 2 3 x
87654321
y
y = ( ) x
3
2
1
0
-1
-2
-3
x
1
2
4
8
-3 -2 -1 0 1 2 3 x
87654321
y
y = 2 x
y = ( ) x
(3,8)
(2,4)
(1,2)
( 0,1)
(-1, )
(-2, )
(-3, )
思考:函数 的图像与 的图像有什么关系 ?可否
利用 的图像画出 的图像 ?
(-3,8)
(-2,4)
(-1,2)
( 0,1)
(2, )
(1, )
(3, )
函数y=2x的图像与 的图像关于y轴对称.
y = ( ) x
x
y
0
y = ( ) x
y = ( ) x
y = 2 x
y = 3 x
思考2:如图四个指数函数图像,当底数大于0小于1和大于1时,图像在画法上有什么特点?
思考3: 通过图像,你能发现指数函数的哪些共同特征?
当底数大于0小于1时,图像自左向右是下降的;
当底数大于1时,图像自左向右是上升的。
1.图像向左、向右是无限延伸的。
2.图像都在x轴的上方。
3.都过定点(0,1)。
(0,1)
2.指数函数 的图像及性质
0
图像
定义域
值域
性 定点
质 单调性
y
x
0
y=1
(0,1)
y
x
0
y=1
(0,1)
(0,+∞)
R
R
(0,+∞)
(0,1) 即 x = 0 时, y = 1 。
在R上是单调增函数
在R上是单调减函数
三、 典例分析
1、已知指数函数
解:因为
所以
故
所以
四、 自作自受
例2.求下列函数的定义域
(1)解:因为
所以
故定义域为:
(2)解:因为
所以
故定义域为:
练2、求下列函数的定义域
四、归纳小结
(1) 通过本节课的学习,你学到了哪些知识?
(2) 你学会了哪些数学思想方法?
1.指数函数的定义以及指数函数的一般表达式的特征;
2.指数函数的图像及其简图的画法;
3.指数函数的性质.
1.数形结合思想;
2.分类讨论思想;
3.从具体到一般的抽象概括的方法。
五、布置作业
课本P58 2 3 P59 5 6
谢谢大家
