2.1.2指数函数的性质与图像 课件(共18张PPT)
文档属性
| 名称 | 2.1.2指数函数的性质与图像 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 815.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 10:41:03 | ||
图片预览





文档简介
(共18张PPT)
2.1.2指数函数及其性质
2.1.2指数函数及其性质
学习目标
理解指数函数的概念
1
画函数图,讨论它的性质
2
用指数函数的性质求定义域
3
用指数函数的性质来比较大小
4
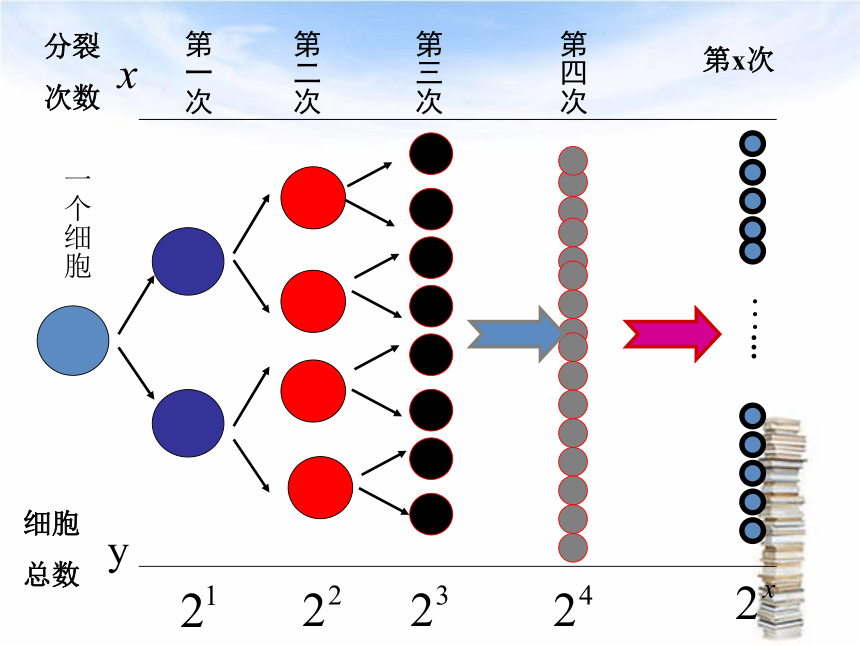
某种细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,第3次由四个分裂成8个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与分裂次数x的函数关系是什么?
思考:
分裂
次数
第一次
第二次
第三次
第四次
第x次
一个细胞
…...
细胞
总数
y
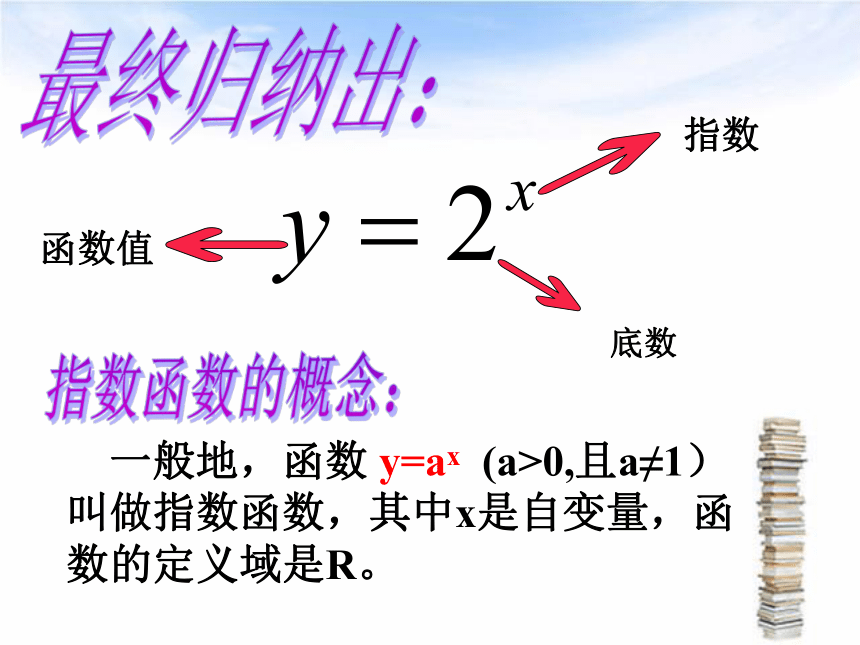
最终归纳出:
指数
底数
函数值
一般地,函数 y=ax (a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
指数函数的概念:
系数为1
函数值
自变量为x
(a 0,且a 1)
a为常数
思考:为何规定a>0且a≠1?
当a 0时,ax有些会没有意义;
当a=1时,函数值y恒等于1,没有研究价值.
例1、判断下列函数哪些是指数函数?
(1) ,
(2) ,
(3) ,
2.指数函数的图象和性质:
回顾:
(1)我们研究函数的性质,通常研究函数的哪些性质?
定义域,值域 ,单调性,奇偶性等。
(2)画函数的图象一目了然(一般方法)?
列表,描点,画图。
在同一个坐标轴上用描点法画出指数函数 和 的图象.
x -2 -1 0 1 2 3
x -3 -2 -1 0 1 2
0.25
0.5
0.5
0.25
0
1
1
底数互为倒数的两个指数函数图象:
关于y轴对称
(0,1)
函数图象
a>1 0图象
定义域
值域
定点
奇偶性
单调性
函数值 分布
y
y=1
O
x
(0,1)
y=1
(0,1)
x
O
y
R
(0, +∞)
(0,1)
非奇非偶函数
在R上是增函数
在R上是减函数
当 x > 0 时,
当 x < 0 时,
y > 1
0< y < 1
当 x < 0 时,
当 x > 0 时,
y > 1
0< y < 1
例题讲解
例2:求下列函数的定义域:
解:
例2: 已知指数函数f(x)的图象经过点(3,π),
求f(0)、f(1)、f(-3)的值.
指数函数的图象经过点 有 ,
即 ,解得
于是有
所以:
分析:设函数
例:3 比较下列各题中两个值的大小:
(1) 1.72.5, 1.73 ;
(2) 0.8-0.1, 0.8-0.2 ;
(3) 1.70.3, 0.93.1;
解:
1.72.5 > 1.73 ;
0.8-0.1< 0.8-0.2 ;
1.70.3 >0.93.1;
比较指数大小的方法:
1.单调性法
2.中间量法
3.图像法
巩固练习:
通过本节课的学习,你学到了哪些知识?
你能熟练应用本节课所学知识解决问题吗?
作业:
课堂小结:
P59页 习题2.1 A组5,7,8
The end,Thank you!
2.1.2指数函数及其性质
2.1.2指数函数及其性质
学习目标
理解指数函数的概念
1
画函数图,讨论它的性质
2
用指数函数的性质求定义域
3
用指数函数的性质来比较大小
4
某种细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,第3次由四个分裂成8个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与分裂次数x的函数关系是什么?
思考:
分裂
次数
第一次
第二次
第三次
第四次
第x次
一个细胞
…...
细胞
总数
y
最终归纳出:
指数
底数
函数值
一般地,函数 y=ax (a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
指数函数的概念:
系数为1
函数值
自变量为x
(a 0,且a 1)
a为常数
思考:为何规定a>0且a≠1?
当a 0时,ax有些会没有意义;
当a=1时,函数值y恒等于1,没有研究价值.
例1、判断下列函数哪些是指数函数?
(1) ,
(2) ,
(3) ,
2.指数函数的图象和性质:
回顾:
(1)我们研究函数的性质,通常研究函数的哪些性质?
定义域,值域 ,单调性,奇偶性等。
(2)画函数的图象一目了然(一般方法)?
列表,描点,画图。
在同一个坐标轴上用描点法画出指数函数 和 的图象.
x -2 -1 0 1 2 3
x -3 -2 -1 0 1 2
0.25
0.5
0.5
0.25
0
1
1
底数互为倒数的两个指数函数图象:
关于y轴对称
(0,1)
函数图象
a>1 0
定义域
值域
定点
奇偶性
单调性
函数值 分布
y
y=1
O
x
(0,1)
y=1
(0,1)
x
O
y
R
(0, +∞)
(0,1)
非奇非偶函数
在R上是增函数
在R上是减函数
当 x > 0 时,
当 x < 0 时,
y > 1
0< y < 1
当 x < 0 时,
当 x > 0 时,
y > 1
0< y < 1
例题讲解
例2:求下列函数的定义域:
解:
例2: 已知指数函数f(x)的图象经过点(3,π),
求f(0)、f(1)、f(-3)的值.
指数函数的图象经过点 有 ,
即 ,解得
于是有
所以:
分析:设函数
例:3 比较下列各题中两个值的大小:
(1) 1.72.5, 1.73 ;
(2) 0.8-0.1, 0.8-0.2 ;
(3) 1.70.3, 0.93.1;
解:
1.72.5 > 1.73 ;
0.8-0.1< 0.8-0.2 ;
1.70.3 >0.93.1;
比较指数大小的方法:
1.单调性法
2.中间量法
3.图像法
巩固练习:
通过本节课的学习,你学到了哪些知识?
你能熟练应用本节课所学知识解决问题吗?
作业:
课堂小结:
P59页 习题2.1 A组5,7,8
The end,Thank you!
