4.1.2指数函数的性质与图像 课件(共104张PPT)
文档属性
| 名称 | 4.1.2指数函数的性质与图像 课件(共104张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览










文档简介
(共104张PPT)
指数函数的性质与图像
第1课时 指数函数的性质与图像
1.指数函数
函数y=ax称为指数函数,其中a是常数,a>0且a≠1.
【思考】
(1)为什么指数函数的底数a>0,且a≠1?
提示:①如果a=0,当x>0时,ax恒等于0,没有研究的必要;当x≤0时,ax无意义.
②如果a<0,例如f(x)=(-4)x,这时对于x= , ,…,
该函数无意义.
③如果a=1,则y=1x是一个常量,没有研究的价值.
为了避免上述各种情况,所以规定a>0,且a≠1.
(2)指数函数的解析式有什么特征?
提示:①a>0,且a≠1;②ax的系数为1;
③自变量x的系数为1.
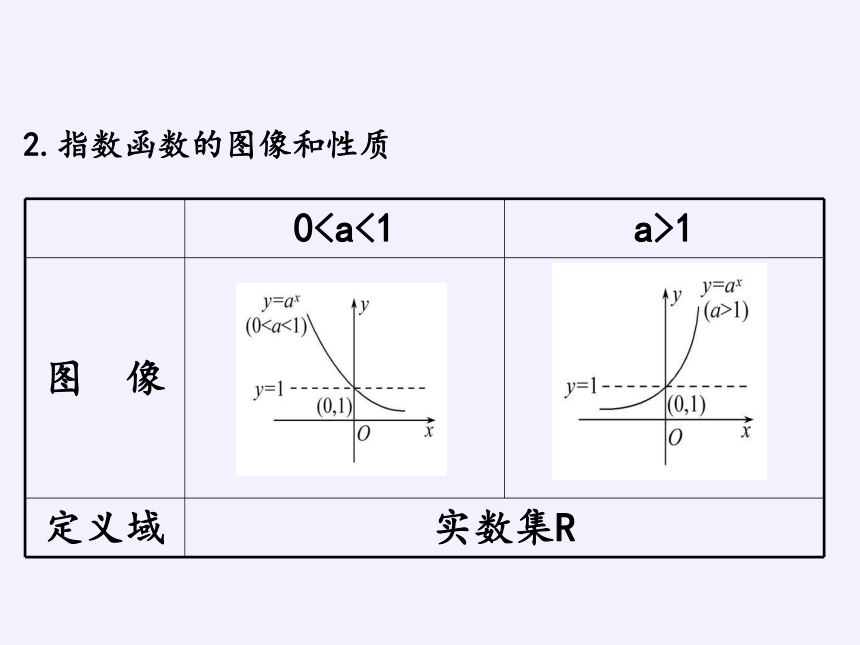
2.指数函数的图像和性质
01
图 像
定义域 实数集R
01
值 域 (0,+∞)
性 质 过定点(0,1)____
是减函数 是增函数
【思考】
(1)对于指数函数y=2x,y=3x,y= ,y= …,为什么一定过点(0,1)?
提示:当x=0时,=1恒成立,即指数函数的图像一定过点(0,1).
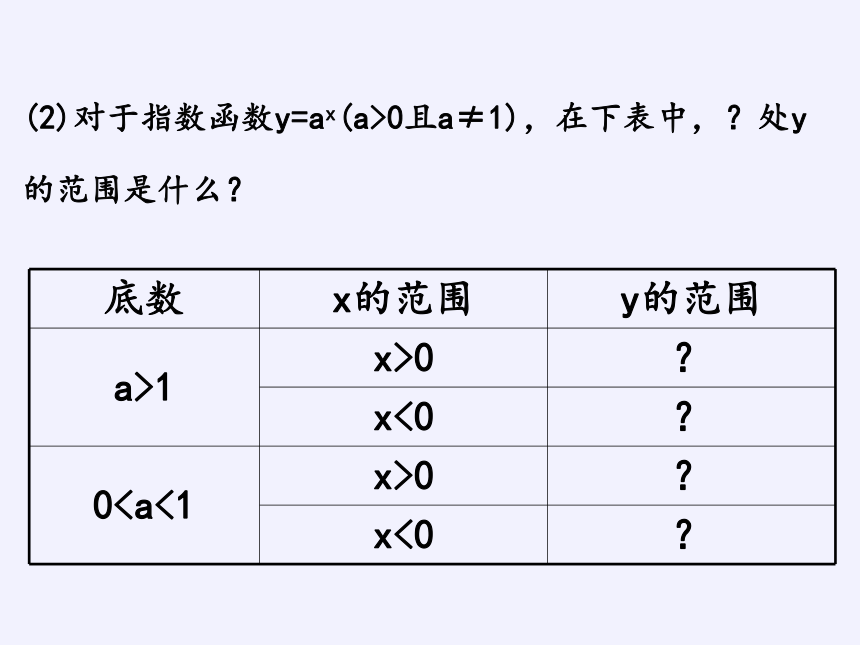
(2)对于指数函数y=ax(a>0且a≠1),在下表中,?处y的范围是什么?
底数 x的范围 y的范围
a>1 x>0 ?
x<0 ?
00 ?
x<0 ?
提示:
底数 x的范围 y的范围
a>1 x>0 y>1
x<0 000 0x<0 y>1
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)y=是指数函数. ( )
(2)指数函数的图像都在x轴的上方. ( )
(3)若指数函数y=ax是减函数,则0提示:(1)×.y=不是指数函数,指数函数的底数是常数.
(2)√.由指数函数的图像可知正确.
(3)√.由指数函数的单调性可知正确.
2.若0A.第一、二象限
B.第二、四象限
C.第一、二、四象限
D.第二、三、四象限
【解析】选A.当03.若函数f(x)是指数函数,且f(2)=2,则f(x)=
________.
【解析】由题意,设f(x)=ax(a>0且a≠1),则由
f(2)=a2=2,得a= ,所以f(x)=( )x.
答案:( )x
类型一 指数函数的概念
【典例】1.函数y=(a2-3a+3)·ax是指数函数,则a的值为________.
2.指数函数y=f(x)的图像经过点(π,e),则f(-π)
=________.
【思维·引】1.根据指数函数的解析式的特征列方程求解.
2.设出指数函数的解析式,代入点的坐标求f(-π).
【解析】1.由题意得a2-3a+3=1,即(a-2)(a-1)=0,解得a=2或a=1(舍).
答案:2
2.设指数函数为y=ax(a>0且a≠1),则e=aπ,所以
f(-π)=a-π=(aπ)-1=e-1= .
答案:
【内化·悟】
怎样设指数函数的解析式?
提示:设指数函数为f(x)=ax(a>0且a≠1).
【类题·通】
1.判断一个函数是指数函数的方法
(1)把握指数函数解析式的特征:①底数a>0,且a≠1;
②ax的系数为1;③自变量x的系数为1.
(2)有些函数需要对解析式变形后判断,如y= 是
指数函数.
2.求指数函数解析式的步骤
(1)设指数函数的解析式f(x)=ax(a>0且a≠1).
(2)利用已知条件求底数a.
(3)写出指数函数的解析式.
【习练·破】
1.函数f(x)=(2a-3)ax是指数函数,则f(1)=( )
A.8 B. C.4 D.2
【解析】选D.函数f(x)=(2a-3)ax是指数函数,
所以2a-3=1,解得a=2,所以f(x)=2x,所以f(1)=2.
2.指数函数y=f(x)的图像经过点 ,那么f(4)·
f(2)=________.
【解析】设指数函数的解析式为y=ax(a>0且a≠1),
因为函数的图像经过点 ,所以 =a-2,所以a=2,所以指数函数的解析式为y=2x,
所以f(4)·f(2)=24×22=26=64.
答案:64
【加练·固】
若指数函数y=f(x)的图像经过点 ,则f
=________.
【解析】设f(x)=ax(a>0且a≠1),因为f(x)过点 ,
所以 =a-2,所以a=4,
所以f(x)=4x,
所以
答案:
类型二 指数函数性质的简单应用
角度 比较大小
【典例】1.(2019·聊城高一检测)已知a=1.50.5,
b=0.51.5,c=0.50.5,则( )
A.a>b>c B.a>c>b
C.b>a>c D.c>a>b
2.使不等式92x-1< 成立的x的集合是( )
【思维·引】1.同底数的利用单调性比较,不同底的与1比较.
2.化同底后利用单调性解不等式.
【解析】1.选B.a=1.50.5>1,0<0.51.5<0.50.5<1,所以a>c>b.
2.选A.不等式即34x-2< ,可得4x-2< ,
解得x< .
【素养·探】
在解与指数相关的不等式时,常常利用核心素养中的逻辑推理,通过对底数单调性的分类讨论来解不等式.
将典例2的不等式底数都改为a(a>0,且a≠1),
即a2x-1< ,试解此不等式.
【解析】当a>1时,指数函数y=ax是增函数,
由2x-1< ,解得x< .
当0 ,解得
x> .
【类题·通】
利用单调性比较大小
(1)底数相同的直接利用单调性.
(2)底数、指数都不同的把1作为中间量比较.
(3)底数不同指数相同的借助图像间的关系比较.
【习练·破】
1.(2019·厦门高一检测)已知a=0.40.3,b=0.30.4,
c=0.3-0.2,则( )
A.bC.c【解析】选A.因为1>a=0.40.3>0.30.3>b=0.30.4,c=
0.3-0.2>1,所以b2.(2019·凯里高一检测)已知a=0.52.1,b=20.5,
c=0.22.1,则a,b,c的大小关系是( )
A.aa>c
C.ba>b
【解析】选B.a=0.52.1∈(0,1),b=20.5>1,c=0.22.1,
0.52.1>0.22.1,所以a>c,所以b>a>c.
【加练·固】
已知 则a,b,c的大小关系是
( )
A.cC.b【解析】选D.对于指数函数y=ax,若x<0,
则当01;当a>1时,有0所以0<
又因为函数y= 在R上是减函数,
且 ,所以 .
综上知, ,即c类型三 与指数函数有关的定义域、值域
【典例】1.函数y= 的定义域是________.
2.函数y=3-x(-2≤x≤1)的值域是 ( )
A.[3,9] B.
C. D.
3.已知函数f(x)=ax(a>0,a≠1)在区间[-1,1]上的最大值与最小值的差是1,则实数a的值为________.
【思维·引】1.根据被开方数大于等于0求定义域.
2.先确定函数的单调性,再求最值.
3.分情况表示出最大值、最小值,列方程求a的值.
【解析】1.因为函数有意义的充要条件是x2-x-6≥0,
即x≤-2或x≥3,
所以所求的定义域为(-∞,-2]∪[3,+∞).
答案: (-∞,-2]∪[3,+∞).
2.选B.函数y=3-x= 在[-2,1]递减,
故=3-(-2)=9,=3-1=
3.当a>1时,y=ax在[-1,1]上单调递增,
所以当x=-1时,y取到最小值a-1,
当x=1时,y取到最大值a,
所以a-a-1=1,解得a= ;
当0所以当x=-1时,y取到最大值a-1,
当x=1时,y取到最小值a,所以a-1-a=1,解得a= .
答案:
【内化·悟】
求值域主要应用了指数函数的哪个性质?
提示:主要应用了指数函数的单调性.
【类题·通】
1.与指数函数相关的定义域问题
(1)函数y=af(x)的定义域与函数f(x)的定义域相同.
(2)涉及不等关系求定义域时,先化同底,再利用图像、单调性求范围.
2.关于指数函数值域的求法
当指数函数的单调性可以确定时,分别求出其最大值、最小值得到函数的值域,若函数的单调性不确定时,则分情况讨论单调性,分别求出其最值,从而确定值域.
【习练·破】
(2019·通州高一检测)函数y= 的定义域为
________.
【解析】依题意得,2x-8≥0,
所以2x≥8=23,又y=2x为增函数,所以x≥3.
所以函数y= 的定义域为{x|x≥3}.
答案:[3,+∞)
【加练·固】
函数y= 的定义域为________.
【解析】因为函数有意义的充要条件是1- ≥0,则
≤1,即x≥0,
所以函数的定义域为[0,+∞).
第2课时
指数函数的性质与图像的应用
类型一 指数函数的图像及应用
【典例】1.(2019·重庆高一检测)函数y= 的大致
图像是( )
2.函数f(x)=ax-2018+2019(a>0且a≠1)所过的定点坐标为________.
【思维·引】1.去掉解析式中的绝对值号,分情况作图.
2.令x-2018=0,求出x,再求f(x).
【解析】1.选C.函数y=
因为y=2-|x|是偶函数,所以图像关于y轴对称,
所以函数图像在y轴右侧为减函数,0左侧为增函数,02.由题意,根据指数函数的性质,令x-2018=0,
可得x=2018,代入求解f(x)=2020,
所以函数f(x)过的定点坐标为(2018,2020).
答案:(2018,2020)
【内化·悟】
1.怎么样作带绝对值号的函数的图像?
提示:去掉绝对值号,分情况作图.
2.形如y=makx+b+n的函数所过的定点坐标是什么?
提示:令kx+b=0,x= ,y=m+n,
所以函数过定点
【类题·通】
与指数函数相关的图像问题
1.定点问题:令函数解析式中的指数为0,即可求出横坐标,再求纵坐标即可;
2.平移问题:对于横坐标x满足“加左减右”;
3.底数大小:对于 如图
0【习练·破】
指数函数①f(x)=mx,②g(x)=nx满足不等式0【解析】选C.由0【加练·固】
函数①y=ax;②y=bx;③y=cx;④y=dx的图像如图所示,a,b,c,d分别是下列四个数: 中的一个,则对应的a,b,c,d的值是( )
【解析】选C.方法一:从第一象限看指数函数的图像,
逆时针方向底数依次从小变大.
方法二:直线x=1与函数图像的交点的纵坐标从上到下
依次为c,d,a,b,而
类型二 形如y= 的函数的单调性、值域
【典例】求函数y= 的单调递增区间、值域.
【思维·引】1.结合y= 的单调性,求二次函数t=-x2+x+2的减区间.
2.利用换元法求值域.
【解析】令t=-x2+x+2,则y= ,
因为t= ,可得t的减区间为 ,因为函
数y= 在R上是减函数,
所以函数y= 的单调递增区间 ;
又t≤ ,所以
所以函数y= 值域为
【类题·通】
复合函数的单调性、值域
(1)分层:一般分为外层y=at,内层t=f(x).
(2)单调性复合:复合法则“同增异减”,即内外层的单调性相同则为增函数,单调性相反则为减函数.
(3)值域复合:先求内层t的值域,再利用单调性求y=at的值域.
【发散·拓】
求函数y=9x-2·3x+3的单调区间,并求出其值域.
【解析】设u=3x,则原函数可分解为u=3x,y=u2-2u+3,
而二次函数y=u2-2u+3单调性的分界点为u=1,
因此当x∈(-∞,0)时,u=3x单调递增,u∈(0,1),而y=u2-2u+3在(0,1)上单调递减,
所以原函数在(-∞,0)上单调递减;当x∈[0,+∞)时,u=3x单调递增,u∈[1,+∞),而二次函数y=u2-2u+3在[1,+∞)上单调递增,所以原函数在[0,+∞)上单调递增.
综上可知,原函数在(-∞,0)上单调递减,在[0,+∞)上单调递增.
函数y=9x-2·3x+3的值域,即y=-2u+3,u∈(0,+∞)的值域,易知值域为[2,+∞).
【延伸·练】
求函数y=22x+1-2x+2-6的单调区间及值域.
【解析】y=22x+1-2x+2-6=2·22x-4·2x-6,
令t=2x(t>0),则y=2t2-4t-6=2(t-1)2-8,
所以在区间[0,1]上递减,在区间[1, +∞)上递增,
因为函数t=2x是增函数,
所以原函数的增区间是[0,+∞),减区间是(-∞,0],
值域是[-8,+∞).
【习练·破】
函数f(x)= 的单调递减区间是________,值域是
________.
【解析】令t=x2-2x=(x-1)2-1,则f(x)= ,利用二次
函数的性质可得函数t的增区间为[1,+∞),所以函数
f(x)= 的减区间是[1,+∞);
因为t≥-1,所以
所以函数f(x)= 的值域为
答案:[1,+∞)
【加练·固】
已知函数y= 的递减区间为________.
【解析】u=x2+2x-3,开口向上,对称轴为x=-1,x∈
(-∞,-1)时函数是减函数;
y=2u,是增函数,由复合函数的单调性可知函数
y= 的递减区间为(-∞,-1).
答案:(-∞,-1)
类型三 指数函数性质的综合应用
角度1 分段函数的单调性
【典例】已知若函数f(x)= 对任意
x1≠x2,都有 >0成立,则实数a的取值范围
是( )
(4,8) B. [4,8)
C. (1,+∞) D. (1,8)
【思维·引】根据函数的单调性,分别从每一段、分界点处函数值的关系列出不等式求范围.
【解析】选B.因为分段函数为增函数,
所以需满足 解得4≤a<8.
【素养·探】
在由分段函数的单调性求参数范围的过程中,常常用到
核心素养中的逻辑推理,根据函数的单调性列出参数满
足的不等式组求出范围.
若将本例中的函数改为f(x)= 其他条
件不变,试求a的范围.
【解析】因为函数f(x)满足对任意x1f(x1)所以函数f(x)在定义域上是增函数,
则满足 即 得 ≤a<2.
角度2 函数性质的综合应用
【典例】(2019·赤峰高一检测)已知函数f(x)=
是R上的奇函数.
(1)判断并证明f(x)的单调性.
(2)若对任意实数,不等式f[f(x)]+f(3-m)>0恒成立,求
m的取值范围.
【思维·引】先求出a的值,再根据定义判断、证明单调性;
利用函数的性质转化不等式,分离出m后求范围.
【解析】(1)因为f(x)为R上的奇函数,
所以f(0)=0,即 =0,由此得a=1,
所以f(x)= ,所以f(x)为R上的增函数.
证明:设x1f(x1)-f(x2)=1-
因为x1所以f(x1)所以f(x)为R上的增函数.
(2)因为f(x)为R上的奇函数.
所以原不等式可化为f[f(x)]>-f(3-m),
即f[f(x)]>f(m-3),
又因为f(x)为R上的增函数,所以f(x)>m-3,
由此可得不等式m立,由2x>0 2x+1>1 0< <2 -2<- <0
2<4- <4,所以m≤2.
【类题·通】
1.关于分段函数y= 的单调性(1)增函数:
均为增函数,且
(2)减函数: 均为减函数,且 .
2.含参数恒成立问题的一种处理方法
将参数分离到左侧,根据不等号恒成立的方向,求出右侧函数的最大值或最小值,即可得到参数的范围.
特别提醒:已知分段函数的单调性求参数的范围时,容易忽视判断分界点处取值的大小.
【习练·破】
(2019·开封高一检测)已知函数f(x)= -2x,则f(x)
( )
A.是奇函数,且在R上是增函数
B.是奇函数,且在R上是减函数
C.是偶函数,且在R上是增函数
D.是偶函数,且在R上是减函数
【解析】选B.f(x)= -2x,
f(-x)=2x- =-f(x),所以f(x)为奇函数,
又因为函数y= 与y=-2x都是减函数,
所以两个减函数之和仍为减函数.
【加练·固】
若函数f(x)= 为R上的增函数,则实数a
的取值范围是( )
A.3≤a<4 B.1C.1【解析】选A.因为函数f(x)在R上为增函数,
所以
解得3≤a<4.
所以实数a的取值范围是3≤a<4.
谢 谢
指数函数的性质与图像
第1课时 指数函数的性质与图像
1.指数函数
函数y=ax称为指数函数,其中a是常数,a>0且a≠1.
【思考】
(1)为什么指数函数的底数a>0,且a≠1?
提示:①如果a=0,当x>0时,ax恒等于0,没有研究的必要;当x≤0时,ax无意义.
②如果a<0,例如f(x)=(-4)x,这时对于x= , ,…,
该函数无意义.
③如果a=1,则y=1x是一个常量,没有研究的价值.
为了避免上述各种情况,所以规定a>0,且a≠1.
(2)指数函数的解析式有什么特征?
提示:①a>0,且a≠1;②ax的系数为1;
③自变量x的系数为1.
2.指数函数的图像和性质
0
图 像
定义域 实数集R
0
值 域 (0,+∞)
性 质 过定点(0,1)____
是减函数 是增函数
【思考】
(1)对于指数函数y=2x,y=3x,y= ,y= …,为什么一定过点(0,1)?
提示:当x=0时,=1恒成立,即指数函数的图像一定过点(0,1).
(2)对于指数函数y=ax(a>0且a≠1),在下表中,?处y的范围是什么?
底数 x的范围 y的范围
a>1 x>0 ?
x<0 ?
0
x<0 ?
提示:
底数 x的范围 y的范围
a>1 x>0 y>1
x<0 0
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)y=是指数函数. ( )
(2)指数函数的图像都在x轴的上方. ( )
(3)若指数函数y=ax是减函数,则0
(2)√.由指数函数的图像可知正确.
(3)√.由指数函数的单调性可知正确.
2.若0
B.第二、四象限
C.第一、二、四象限
D.第二、三、四象限
【解析】选A.当0
________.
【解析】由题意,设f(x)=ax(a>0且a≠1),则由
f(2)=a2=2,得a= ,所以f(x)=( )x.
答案:( )x
类型一 指数函数的概念
【典例】1.函数y=(a2-3a+3)·ax是指数函数,则a的值为________.
2.指数函数y=f(x)的图像经过点(π,e),则f(-π)
=________.
【思维·引】1.根据指数函数的解析式的特征列方程求解.
2.设出指数函数的解析式,代入点的坐标求f(-π).
【解析】1.由题意得a2-3a+3=1,即(a-2)(a-1)=0,解得a=2或a=1(舍).
答案:2
2.设指数函数为y=ax(a>0且a≠1),则e=aπ,所以
f(-π)=a-π=(aπ)-1=e-1= .
答案:
【内化·悟】
怎样设指数函数的解析式?
提示:设指数函数为f(x)=ax(a>0且a≠1).
【类题·通】
1.判断一个函数是指数函数的方法
(1)把握指数函数解析式的特征:①底数a>0,且a≠1;
②ax的系数为1;③自变量x的系数为1.
(2)有些函数需要对解析式变形后判断,如y= 是
指数函数.
2.求指数函数解析式的步骤
(1)设指数函数的解析式f(x)=ax(a>0且a≠1).
(2)利用已知条件求底数a.
(3)写出指数函数的解析式.
【习练·破】
1.函数f(x)=(2a-3)ax是指数函数,则f(1)=( )
A.8 B. C.4 D.2
【解析】选D.函数f(x)=(2a-3)ax是指数函数,
所以2a-3=1,解得a=2,所以f(x)=2x,所以f(1)=2.
2.指数函数y=f(x)的图像经过点 ,那么f(4)·
f(2)=________.
【解析】设指数函数的解析式为y=ax(a>0且a≠1),
因为函数的图像经过点 ,所以 =a-2,所以a=2,所以指数函数的解析式为y=2x,
所以f(4)·f(2)=24×22=26=64.
答案:64
【加练·固】
若指数函数y=f(x)的图像经过点 ,则f
=________.
【解析】设f(x)=ax(a>0且a≠1),因为f(x)过点 ,
所以 =a-2,所以a=4,
所以f(x)=4x,
所以
答案:
类型二 指数函数性质的简单应用
角度 比较大小
【典例】1.(2019·聊城高一检测)已知a=1.50.5,
b=0.51.5,c=0.50.5,则( )
A.a>b>c B.a>c>b
C.b>a>c D.c>a>b
2.使不等式92x-1< 成立的x的集合是( )
【思维·引】1.同底数的利用单调性比较,不同底的与1比较.
2.化同底后利用单调性解不等式.
【解析】1.选B.a=1.50.5>1,0<0.51.5<0.50.5<1,所以a>c>b.
2.选A.不等式即34x-2< ,可得4x-2< ,
解得x< .
【素养·探】
在解与指数相关的不等式时,常常利用核心素养中的逻辑推理,通过对底数单调性的分类讨论来解不等式.
将典例2的不等式底数都改为a(a>0,且a≠1),
即a2x-1< ,试解此不等式.
【解析】当a>1时,指数函数y=ax是增函数,
由2x-1< ,解得x< .
当0
x> .
【类题·通】
利用单调性比较大小
(1)底数相同的直接利用单调性.
(2)底数、指数都不同的把1作为中间量比较.
(3)底数不同指数相同的借助图像间的关系比较.
【习练·破】
1.(2019·厦门高一检测)已知a=0.40.3,b=0.30.4,
c=0.3-0.2,则( )
A.b
0.3-0.2>1,所以b
c=0.22.1,则a,b,c的大小关系是( )
A.a
C.b
【解析】选B.a=0.52.1∈(0,1),b=20.5>1,c=0.22.1,
0.52.1>0.22.1,所以a>c,所以b>a>c.
【加练·固】
已知 则a,b,c的大小关系是
( )
A.c
则当0
又因为函数y= 在R上是减函数,
且 ,所以 .
综上知, ,即c
【典例】1.函数y= 的定义域是________.
2.函数y=3-x(-2≤x≤1)的值域是 ( )
A.[3,9] B.
C. D.
3.已知函数f(x)=ax(a>0,a≠1)在区间[-1,1]上的最大值与最小值的差是1,则实数a的值为________.
【思维·引】1.根据被开方数大于等于0求定义域.
2.先确定函数的单调性,再求最值.
3.分情况表示出最大值、最小值,列方程求a的值.
【解析】1.因为函数有意义的充要条件是x2-x-6≥0,
即x≤-2或x≥3,
所以所求的定义域为(-∞,-2]∪[3,+∞).
答案: (-∞,-2]∪[3,+∞).
2.选B.函数y=3-x= 在[-2,1]递减,
故=3-(-2)=9,=3-1=
3.当a>1时,y=ax在[-1,1]上单调递增,
所以当x=-1时,y取到最小值a-1,
当x=1时,y取到最大值a,
所以a-a-1=1,解得a= ;
当0
当x=1时,y取到最小值a,所以a-1-a=1,解得a= .
答案:
【内化·悟】
求值域主要应用了指数函数的哪个性质?
提示:主要应用了指数函数的单调性.
【类题·通】
1.与指数函数相关的定义域问题
(1)函数y=af(x)的定义域与函数f(x)的定义域相同.
(2)涉及不等关系求定义域时,先化同底,再利用图像、单调性求范围.
2.关于指数函数值域的求法
当指数函数的单调性可以确定时,分别求出其最大值、最小值得到函数的值域,若函数的单调性不确定时,则分情况讨论单调性,分别求出其最值,从而确定值域.
【习练·破】
(2019·通州高一检测)函数y= 的定义域为
________.
【解析】依题意得,2x-8≥0,
所以2x≥8=23,又y=2x为增函数,所以x≥3.
所以函数y= 的定义域为{x|x≥3}.
答案:[3,+∞)
【加练·固】
函数y= 的定义域为________.
【解析】因为函数有意义的充要条件是1- ≥0,则
≤1,即x≥0,
所以函数的定义域为[0,+∞).
第2课时
指数函数的性质与图像的应用
类型一 指数函数的图像及应用
【典例】1.(2019·重庆高一检测)函数y= 的大致
图像是( )
2.函数f(x)=ax-2018+2019(a>0且a≠1)所过的定点坐标为________.
【思维·引】1.去掉解析式中的绝对值号,分情况作图.
2.令x-2018=0,求出x,再求f(x).
【解析】1.选C.函数y=
因为y=2-|x|是偶函数,所以图像关于y轴对称,
所以函数图像在y轴右侧为减函数,0
可得x=2018,代入求解f(x)=2020,
所以函数f(x)过的定点坐标为(2018,2020).
答案:(2018,2020)
【内化·悟】
1.怎么样作带绝对值号的函数的图像?
提示:去掉绝对值号,分情况作图.
2.形如y=makx+b+n的函数所过的定点坐标是什么?
提示:令kx+b=0,x= ,y=m+n,
所以函数过定点
【类题·通】
与指数函数相关的图像问题
1.定点问题:令函数解析式中的指数为0,即可求出横坐标,再求纵坐标即可;
2.平移问题:对于横坐标x满足“加左减右”;
3.底数大小:对于 如图
0
指数函数①f(x)=mx,②g(x)=nx满足不等式0
函数①y=ax;②y=bx;③y=cx;④y=dx的图像如图所示,a,b,c,d分别是下列四个数: 中的一个,则对应的a,b,c,d的值是( )
【解析】选C.方法一:从第一象限看指数函数的图像,
逆时针方向底数依次从小变大.
方法二:直线x=1与函数图像的交点的纵坐标从上到下
依次为c,d,a,b,而
类型二 形如y= 的函数的单调性、值域
【典例】求函数y= 的单调递增区间、值域.
【思维·引】1.结合y= 的单调性,求二次函数t=-x2+x+2的减区间.
2.利用换元法求值域.
【解析】令t=-x2+x+2,则y= ,
因为t= ,可得t的减区间为 ,因为函
数y= 在R上是减函数,
所以函数y= 的单调递增区间 ;
又t≤ ,所以
所以函数y= 值域为
【类题·通】
复合函数的单调性、值域
(1)分层:一般分为外层y=at,内层t=f(x).
(2)单调性复合:复合法则“同增异减”,即内外层的单调性相同则为增函数,单调性相反则为减函数.
(3)值域复合:先求内层t的值域,再利用单调性求y=at的值域.
【发散·拓】
求函数y=9x-2·3x+3的单调区间,并求出其值域.
【解析】设u=3x,则原函数可分解为u=3x,y=u2-2u+3,
而二次函数y=u2-2u+3单调性的分界点为u=1,
因此当x∈(-∞,0)时,u=3x单调递增,u∈(0,1),而y=u2-2u+3在(0,1)上单调递减,
所以原函数在(-∞,0)上单调递减;当x∈[0,+∞)时,u=3x单调递增,u∈[1,+∞),而二次函数y=u2-2u+3在[1,+∞)上单调递增,所以原函数在[0,+∞)上单调递增.
综上可知,原函数在(-∞,0)上单调递减,在[0,+∞)上单调递增.
函数y=9x-2·3x+3的值域,即y=-2u+3,u∈(0,+∞)的值域,易知值域为[2,+∞).
【延伸·练】
求函数y=22x+1-2x+2-6的单调区间及值域.
【解析】y=22x+1-2x+2-6=2·22x-4·2x-6,
令t=2x(t>0),则y=2t2-4t-6=2(t-1)2-8,
所以在区间[0,1]上递减,在区间[1, +∞)上递增,
因为函数t=2x是增函数,
所以原函数的增区间是[0,+∞),减区间是(-∞,0],
值域是[-8,+∞).
【习练·破】
函数f(x)= 的单调递减区间是________,值域是
________.
【解析】令t=x2-2x=(x-1)2-1,则f(x)= ,利用二次
函数的性质可得函数t的增区间为[1,+∞),所以函数
f(x)= 的减区间是[1,+∞);
因为t≥-1,所以
所以函数f(x)= 的值域为
答案:[1,+∞)
【加练·固】
已知函数y= 的递减区间为________.
【解析】u=x2+2x-3,开口向上,对称轴为x=-1,x∈
(-∞,-1)时函数是减函数;
y=2u,是增函数,由复合函数的单调性可知函数
y= 的递减区间为(-∞,-1).
答案:(-∞,-1)
类型三 指数函数性质的综合应用
角度1 分段函数的单调性
【典例】已知若函数f(x)= 对任意
x1≠x2,都有 >0成立,则实数a的取值范围
是( )
(4,8) B. [4,8)
C. (1,+∞) D. (1,8)
【思维·引】根据函数的单调性,分别从每一段、分界点处函数值的关系列出不等式求范围.
【解析】选B.因为分段函数为增函数,
所以需满足 解得4≤a<8.
【素养·探】
在由分段函数的单调性求参数范围的过程中,常常用到
核心素养中的逻辑推理,根据函数的单调性列出参数满
足的不等式组求出范围.
若将本例中的函数改为f(x)= 其他条
件不变,试求a的范围.
【解析】因为函数f(x)满足对任意x1
则满足 即 得 ≤a<2.
角度2 函数性质的综合应用
【典例】(2019·赤峰高一检测)已知函数f(x)=
是R上的奇函数.
(1)判断并证明f(x)的单调性.
(2)若对任意实数,不等式f[f(x)]+f(3-m)>0恒成立,求
m的取值范围.
【思维·引】先求出a的值,再根据定义判断、证明单调性;
利用函数的性质转化不等式,分离出m后求范围.
【解析】(1)因为f(x)为R上的奇函数,
所以f(0)=0,即 =0,由此得a=1,
所以f(x)= ,所以f(x)为R上的增函数.
证明:设x1
因为x1
(2)因为f(x)为R上的奇函数.
所以原不等式可化为f[f(x)]>-f(3-m),
即f[f(x)]>f(m-3),
又因为f(x)为R上的增函数,所以f(x)>m-3,
由此可得不等式m
2<4- <4,所以m≤2.
【类题·通】
1.关于分段函数y= 的单调性(1)增函数:
均为增函数,且
(2)减函数: 均为减函数,且 .
2.含参数恒成立问题的一种处理方法
将参数分离到左侧,根据不等号恒成立的方向,求出右侧函数的最大值或最小值,即可得到参数的范围.
特别提醒:已知分段函数的单调性求参数的范围时,容易忽视判断分界点处取值的大小.
【习练·破】
(2019·开封高一检测)已知函数f(x)= -2x,则f(x)
( )
A.是奇函数,且在R上是增函数
B.是奇函数,且在R上是减函数
C.是偶函数,且在R上是增函数
D.是偶函数,且在R上是减函数
【解析】选B.f(x)= -2x,
f(-x)=2x- =-f(x),所以f(x)为奇函数,
又因为函数y= 与y=-2x都是减函数,
所以两个减函数之和仍为减函数.
【加练·固】
若函数f(x)= 为R上的增函数,则实数a
的取值范围是( )
A.3≤a<4 B.1
所以
解得3≤a<4.
所以实数a的取值范围是3≤a<4.
谢 谢
