物理人教版(2019)选择性必修第一册1.2动量定理(共67张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.2动量定理(共67张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 98.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-05 19:12:23 | ||
图片预览








文档简介
(共67张PPT)
课堂引入
这些不同的生活现象中隐藏着怎样的物理规律?
一锤下去,是“蛋碎瓦全”,还是“瓦碎蛋全”呢?
课堂引入
课堂引入
为什么鸡蛋会完好无损呢?
课堂引入
第一章 动量守恒定律
第2节 动量定理
新教材人教版 物理(选择性必修第一册)
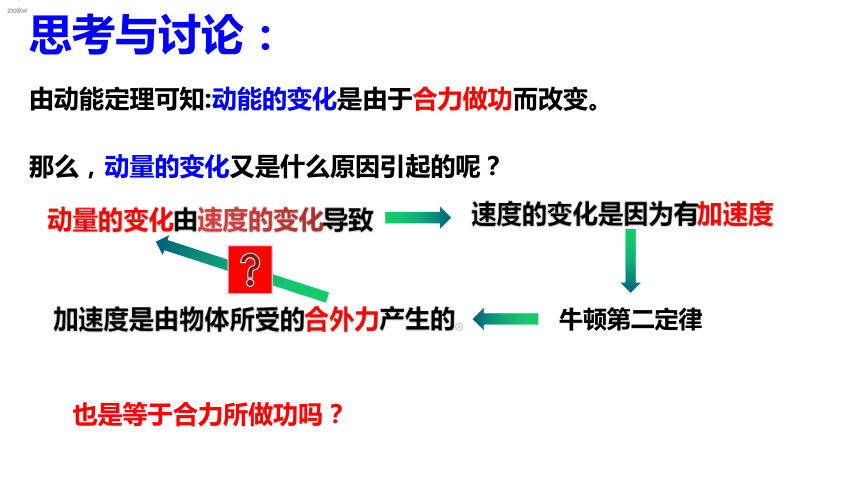
由动能定理可知:动能的变化是由于合力做功而改变。
加速度是由物体所受的合外力产生的。
那么,动量的变化又是什么原因引起的呢?
动量的变化由速度的变化导致
速度的变化是因为有加速度
也是等于合力所做功吗?
思考与讨论:
牛顿第二定律
设置物理情景:质量为m 的物体,在合力F 的作用下,经过一段时间 Δt,速度由v 变为v′,如图所示:
由牛顿第二定律:
加速度定义:
F = ma
则有:
即:
表明动量的变化与力的作用对时间的积累效果有关。
冲量
力是产生加速度的原因,
力也称作动量变化率。
合力越大动量变化越快。
1.定义:力F 与作用时间Δt 的乘积叫作力的冲量,用字母I 表示冲量。
2.公式:
4.矢量:
5.物理意义:
3.单位:
I=F·Δt (F 为恒力)
在国际单位制中,冲量的单位是牛·秒,符号是N·s
冲量的方向由力的方向决定。
若为恒定方向的力,则冲量的方向跟这力的方向相同。
反映力的作用对时间的积累效应。
一、冲量
注意:有力作用于物体,该力一定产生冲量,
但不一定做功;力对物体做了功,一定有冲量。
过程量
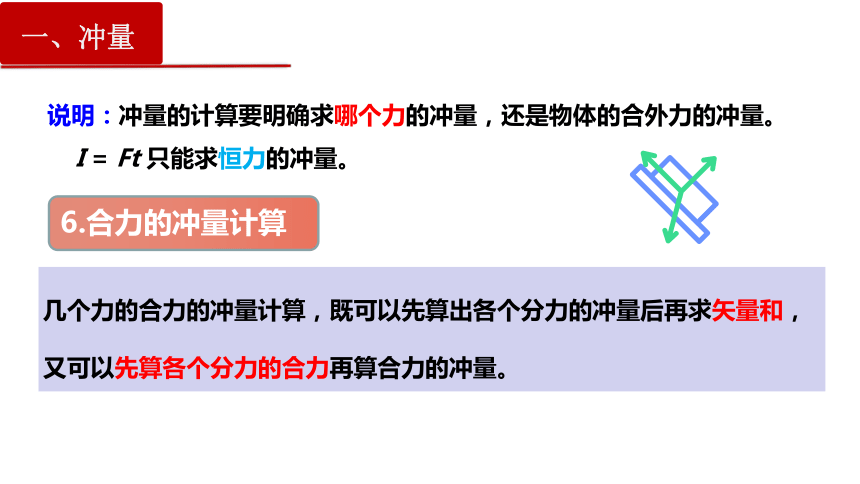
6.合力的冲量计算
说明:冲量的计算要明确求哪个力的冲量,还是物体的合外力的冲量。
I = Ft 只能求恒力的冲量。
几个力的合力的冲量计算,既可以先算出各个分力的冲量后再求矢量和,又可以先算各个分力的合力再算合力的冲量。
一、冲量
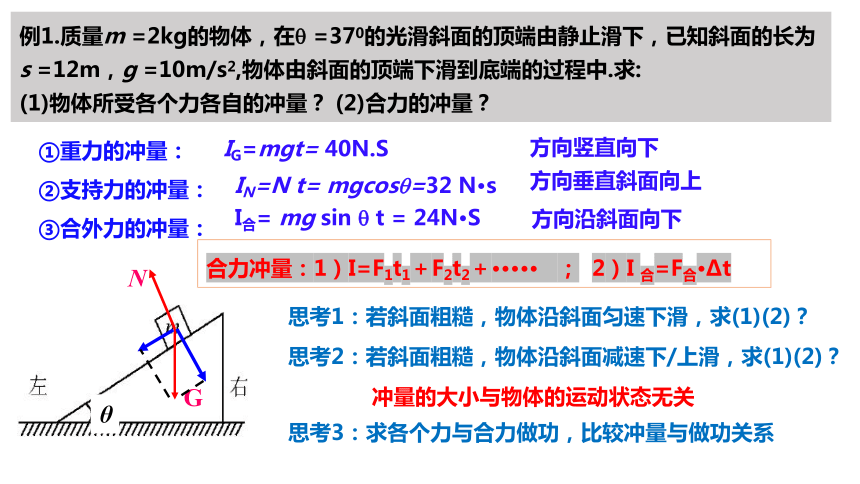
例1.质量m =2kg的物体,在 =370的光滑斜面的顶端由静止滑下,已知斜面的长为s =12m,g =10m/s2,物体由斜面的顶端下滑到底端的过程中.求:
(1)物体所受各个力各自的冲量? (2)合力的冲量?
θ
G
N
IG=mgt= 40N.S
方向竖直向下
IN=N t= mgcos =32 N·s
方向垂直斜面向上
I合= mg sin t = 24N·S
方向沿斜面向下
①重力的冲量:
②支持力的冲量:
③合外力的冲量:
冲量的大小与物体的运动状态无关
合力冲量:1)I=F1t1+F2t2+····· ; 2)I 合=F合·Δt
思考1:若斜面粗糙,物体沿斜面匀速下滑,求(1)(2)?
思考2:若斜面粗糙,物体沿斜面减速下/上滑,求(1)(2)?
思考3:求各个力与合力做功,比较冲量与做功关系
冲量 功
区别 意义
公式
单位
标矢量
正负
作用效果
联系
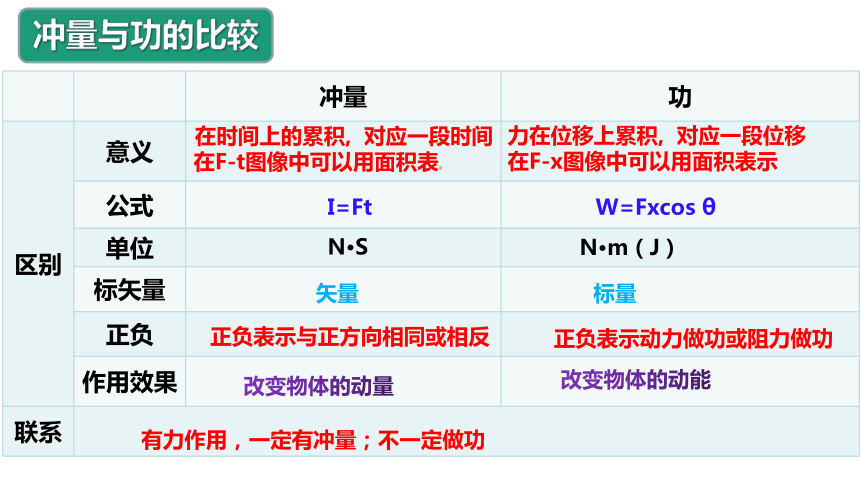
冲量与功的比较
改变物体的动量
改变物体的动能
W=Fxcos θ
I=Ft
力在时间上的累积, 对应一段时间
在F-t图像中可以用面积表示
力在位移上累积, 对应一段位移
在F-x图像中可以用面积表示
N·S
N·m(J)
矢量
标量
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
有力作用,一定有冲量;不一定做功
有了冲量的概念,FΔt= p′ - p 其表达式也可以写成:
这表明:物体在一个过程中所受力的冲量等于它在这个过程始末的动量变化量,这个关系叫作动量定理。
I=p′-p 或者 F(t′-t)=mv′-mv
二、动量定理
1.内容:物体在一个过程中所受力的冲量等于它始末的动量变化量。
2.表达式:
①“力的冲量”是指合力的冲量,可以是恒力,可以是变力.
②表明合外力的冲量是动量变化的原因;
③ 动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同。
④动量的变化率:动量的变化跟发生这一变化所用的时间的比值。由动量定理,得 ,可见,动量的变化率等于物体所受的合力。
I=p′-p 或 FΔt = mv′-mv
3.理解:
二、动量定理
动量定理的优点:不考虑中间过程,只考虑初末状态。
三、动量定理
4.动量定理的适用范围:
①适用于恒力,也适用变力(平均值);
②可以解决匀变速直线运动,还可以解决曲线运动
③仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
例题:一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间 为0.01s。球棒对垒球的平均作用力是多大?
解析:垒球的初动量为
p=mv=0.18×25 kg·m/s=4.5kg·m/s
垒球的末动量为
pˊ=mvˊ=(-0.18)×25 kg·m/s= - 8.1kg·m/s
由动量定理知垒球所受的平均作用力为
负号表示力的方向与垒球飞来的方向相反
二、动量定理
动量定理的应用步骤
1.确定研究对象:一般为单个物体;
4.选定正方向,确定在物理过程中研究对象的动量的变化;
5.根据动量定理列方程,统一单位后代入数据求解。
2.明确物理过程:受力分析,求出合外力的冲量;
3.明确研究对象的初末状态及相应的动量;
例:一个质量 m=2 kg 的物体,静止在光滑的水平地面上,某时刻受到F=10N的水平力的作用,经历t=5 s的时间。(g 为 10 m/s2)求 :
(1)重力的冲量; (2)支持力的冲量;(3)外力F的冲量;(4)合力的冲量。
解:(1)IG=Gt=100 N·s ;(2)IFN=FNt=100 N·s ;(3)IF= Ft =50 N·s 。
(4)合力的冲量。
法一:I合=IG+IFN+IF(矢量叠加)
I合=IF=50 N·s
法二:I合=F合 t
=Ft =50 N·s
法三:动量定理
I合=p′-p=mv′-mv
法一:先算出各个分力的冲量后再求矢量和。
总结:合力的冲量计算方法
法二:先算各个分力的合力再算合力的冲量。
法三:利用动量定理计算合力的冲量。
类比合力的功计算方法
(1)落地时vy2=2gh=10m/s
所以v=√v02+vy2=10√2m/s
则P=mv=10√2kgm/s,
(2)Δp=√p2-p02=10kgm/s,
例题:一个质量为 1 kg 的物体从距地面高为h=5m处以v0=10m/s的水平初速度抛出g=10m/s2.求:
(1)落地时动量
(2) 下落过程中动量的变化量
解:
(1)初末动量不共线时,动量变化只能矢量运算
(2)求动量、动量变化、冲量时,要作方向说明
与水平地面成夹角45°
方向竖直向下
例题:在撑竿跳比赛的横杆下方要放上很厚的海绵垫子.设一位撑竿跳运动员的质量为70 kg,越过横杆后从h=5.6 m高处落下,落在海绵垫上经历时间Δt=1 s停下.求海绵垫对运动员的作用力.(g=10m/s2)
解:下落到静止,以竖直向下为正方向
据动量定理可知:IG+IF=ΔP=0 ---①
自由落体过程:h=gt2/2 ---②
即:mg(t+Δt)+FΔt=0 ---③
代入数据解①②③得:F=-1441N,方向竖直向上
(1)多过程可全程立式求解
(2)动量的变化等于合力的冲量,不是某一个力的冲量
(3)多力共线时,合力冲量时可直接代数运算
将该段时间
无限分割
F
t/s
4
3
2
1
0
2
4
6
10
8
t/s
4
3
2
1
0
2
4
6
10
8
F
t/s
4
3
2
1
0
2
4
6
10
8
F
一段时间内的变力
近似认为物体在每一时段以受到某一恒力
一段时间内的变力的冲量
微分求和
由图可知F-t图线与时间轴之间所围的“面积”的大小表示对应时间t0内,力F0的冲量的大小。
微元法
思考
如果一个力随时间不断变化,又该怎样求冲量?
①变力的冲量通常可利用动量定理 I=Δp 求解
②可用图象法计算冲量。阴影部分的面积就表示力在时间Δt=t2-t1内的冲量。
③对于方向不变、大小随时间均匀变化的变力,冲量也可用I=F(t'-t)计算,但式中的F应为Δt时间内的平均力,即
微元法
变力的冲量计算方法
如何运用动量定理解释生活中的相关现象?
思考
1.跳高比赛中为什么要垫海绵垫?
2.与直接落在地面上什么相同?什么不同?
增大运动员落地减速过程的作用时间,减小冲击力
动量变化Δp相同,减速过程作用时间Δt不同,合力F合不同,冲击力F不同
1.解释有关现象
透过现象看本质——探究物理规律
越长,
一定,
越短,
则F越小.
则F越大.
一定,
例:(2018全国卷II)若一个50 g的鸡蛋从20m坠下,与地面的撞击时间约为0.001s,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102 N C.103 N D.104 N
C
思考:若地面平铺一层海绵,使得撞击时间变为0.1s,冲击力?
10N
——缓冲作用
四、动量定理的应用
2.用锤子使劲压钉子,就很难把钉子压入木块中去,如果用锤子以一定的速度敲钉子,钉子就很容易钻入木块,这是为什么?
3.1980年,一架英国的“鸽式”战斗机在威夫士地区上空与一只秃鹰相撞,飞机坠毁,飞行员弹射逃生……
小小飞禽何以能撞毁飞机这样的庞然大物?
四、动量定理的应用
1.解释有关现象
②t一定,F大则△P大,F小则△P小;
③F一定,t长则△P大,t短则△P小。
例:对于力的冲量,下列说法正确的是 ( )
A. 力越大,力的冲量就越大;
B. 作用在物体上的力大,力的冲量不一定大;
C. 力与位移垂直时,力的冲量为零;
D. 物体在水平推力作用下, 经一段时间t后仍处于静止状态,则此推力的冲量为零。
B
四、动量定理的应用
例:(2020全国卷1)行驶中的汽车如果发生剧烈碰撞,车内的安全气囊会被弹出并瞬间充满气体。若碰撞后汽车的速度在很短时间内减小为零,关于安全气囊在此过程中的作用,下列说法正确的是( )
A.增加了司机单位面积的受力大小
B.减少了碰撞前后司机动量的变化量
C.将司机的动能全部转换成汽车的动能
D.延长了司机的受力时间并增大了司机的受力面积
D
玻璃杯掉在坚硬的地面上很容易摔碎,掉在地毯上就不容易摔碎。
四、动量定理的应用
快递包装用的材料
四、动量定理的应用
消防救生气垫
船靠岸时边缘上的废旧轮胎
四、动量定理的应用
为什么鸡蛋会完好无损呢?
四、动量定理的应用
STSE
1.汽车的碰撞试验
1)汽车的安全气囊的保护作用
2)轿车前面的发动机舱并不是越坚固越好
带气垫的运动鞋
下落时屈膝
课堂小结
01
02
03
动量定理
动量定理:物体所受合外力的冲量等于物体的动量变化,这就是动量定理。
动量定理
的应用
动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同;
冲量
冲量:作用在物体上的力和作用时间的乘积,叫做该力对这个物体的冲量I
冲量是矢量,过程量,反映了力对时间的积累效应.
I=Ft
1.如图,一物体静止在水平地面上,受到与水平方向成 θ 角的恒定拉力 F 作用时间 t 后,物体仍保持静止。现有以下看法:
A.物体所受拉力 F 的冲量方向水平向右
B.物体所受拉力 F 的冲量大小是 Ft cos θ
C.物体所受摩擦力的冲量大小为 0
D.物体所受合力的冲量大小为 0
你认为这些看法正确吗?请简述你的理由。
练习与应用 P10
解析:A.错误,物体所受拉力的冲量方向与拉力方向相同;B.错误,物体所受拉力的冲量大小为 Ft ;C.错误,物体所受摩擦力的冲量大小为 Ft cos θ ;D.正确,物体静止,所以物体所受合力大小为零,物体所受合力的冲量大小为 0 。
2.体操运动员在落地时总要屈腿,这是为什么?
答:体操运动员落地时的动量是一定的,在落地过程中,动量的变化量一定。由动量定理可知,运动员受到的冲量 I 一定;由 I=Ft 可知,体操运动员在着地时屈腿可以延长作用时间 t ,可以减小运动员所受的平均冲力 F 。
练习与应用 P10
3.如图,用 0.5 kg 的铁锤钉钉子。打击前铁锤的速度为 4 m/s ,打击后铁锤的速度变为 0 ,设打击时间为 0.01 s ,g 取10 m/s2 。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,在什么情况下可
以不计铁锤所受的重力。
练习与应用 P10
解析:
(1)不考虑铁锤的重力,铁锤只受到钉子的作用力,由动量定理得:
Ft=mv,代入数据得:F=200 N 。
根据牛顿第三定律,铁锤对钉子的作用力为 F′=F=200 N ;
3.如图,用 0.5 kg 的铁锤钉钉子。打击前铁锤的速度为 4 m/s ,打击后铁锤的速度变为 0 ,设打击时间为 0.01 s ,g 取10 m/s2 。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,在什么情况下可
以不计铁锤所受的重力。
练习与应用 P10
解析:
(2)考虑铁锤的重力,对铁锤,由动量定理可得:(F-mg)t=mv,
代入数据可得:F=205 N 。
根据牛顿第三定律,铁锤对钉子的作用力 F′=F=205 N ;
3.如图,用 0.5 kg 的铁锤钉钉子。打击前铁锤的速度为 4 m/s ,打击后铁锤的速度变为 0 ,设打击时间为 0.01 s ,g 取10 m/s2 。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,在什么情况下可
以不计铁锤所受的重力。
练习与应用 P10
解析:
(3)根据(1)和(2)两问铁锤对钉子的作用力可知,205 N 比 200 N 大 5 N,为 ×100%=2.4 % ,由此可知,当作用时间比较小的时候,铁锤的重力可以忽略不计。
4. 一个质量为 10 kg 的物体,以 10 m/s 的速度做直线运动,受到一个反向的作用力 F,经过 4 s,速度变为反向 2 m/s。这个力是多大?
练习与应用 P10
解析:取初速度方向为正方向,设这个理的大小为F,根据题意,由动量定理得:
解得:
5. 一个质量为 60 kg 的蹦床运动员,从离水平网面 3.2 m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0 m 高处。已知运动员与网接触的时间为 0.8 s,g 取 10 m/s2。
(1)求运动员与网接触的这段时间内动量的变化量。
(2)求网对运动员的平均作用力大小。
(3)求从自由下落开始到蹦回离水平网面5.0 m 高处这一过程中运动员所受重力的冲量、弹力的冲量。
练习与应用 P10
解析:
(1)向下接触网面的速度为:
向上离开网面的速度为:
向上为正,动量的变化量为
5. 一个质量为 60 kg 的蹦床运动员,从离水平网面 3.2 m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0 m 高处。已知运动员与网接触的时间为 0.8 s,g 取 10 m/s2。
(1)求运动员与网接触的这段时间内动量的变化量。
(2)求网对运动员的平均作用力大小。
(3)求从自由下落开始到蹦回离水平网面5.0 m 高处这一过程中运动员所受重力的冲量、弹力的冲量。
练习与应用 P10
解析:
(2)网对运动员的平均作用力为F,根据动量定理:
代入数据解得:F=1950N
5. 一个质量为 60 kg 的蹦床运动员,从离水平网面 3.2 m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0 m 高处。已知运动员与网接触的时间为 0.8 s,g 取 10 m/s2。
(1)求运动员与网接触的这段时间内动量的变化量。
(2)求网对运动员的平均作用力大小。
(3)求从自由下落开始到蹦回离水平网面5.0 m 高处这一过程中运动员所受重力的冲量、弹力的冲量。
练习与应用 P10
解析:(3)向下接触网面的时间为:
向上运动到最高的时间为:
重力的冲量:
弹力的冲量:
6. 曾经有一则新闻报道,一名 4 岁儿童从3 层高的楼房掉下来,被一名见义勇为的青年接住。请你估算一下,儿童受到的合力的冲量是多大?设儿童与青年之间的相互作用时间为 0.1 s,则儿童受到的合力的平均值有多大?
练习与应用 P10
解析:取向下为正方向,设儿童的质量为m= 20kg ,g =10m/s2。
第三层楼的地板离地面高为h=6m,儿童落地时的速度为v,
由v2= 2gh得,v= √2gh。
儿童被青年接住的过程中,设儿童受到的合力的冲量为I,由动量定理得:
I=0 - mv = -m√2gh≈ -219.1N S,
设儿童受到的合力的平均值为F,由动量定理得I=Ft,其中t =0.1s,
解得:F =-2191N,所以合力的平均值为2191N,方向为竖直向上。
1.(多选)关于冲量和动量,下列说法中正确的是( )
A.冲量是反映力的作用时间积累效果的物理量
B.动量是描述物体运动状态的物理量
C.冲量是物体动量变化的原因
D.冲量是描述物体状态的物理量
ABC
当堂检测
2.甲乙两个质量相同的物体,以相同的初速度分别在粗糙程度不同的水平面上运动,乙物体先停下来,甲物体又经较长时间停下来,正确的是( )
A.甲物体受到的冲量大
B.乙物体受到的冲量大
C.两个物体受到的冲量大小相等
D.无法判断
C
当堂检测
3.(多选)在任何相等的时间内,物体动量变化量相等的运动是( )
A.竖直上抛运动 B.匀速圆周运动
C.自由落体运动 D.平抛运动
ACD
当堂检测
4.(多选)(2017·高考全国卷Ⅲ)一质量为 2 kg 的物块在合外力F 的作用下从静止开始沿直线运动。F 随时间t 变化的图线如图所示,则( )A.t=1 s时物块的速率为1 m/sB.t=2 s时物块的动量大小为4 kg·m/sC.t=3 s时物块的动量大小为5 kg·m/sD.t=4 s时物块的速度为零
当堂检测
AB
5.(多选)长征途中,为了突破敌方关隘,战士爬上陡销的山头,居高临下向敌方工事内投掷手榴弹,战士在同一位置先后投出甲、乙两颗质量均为m的手榴弹,手榴弹从投出的位置到落地点的高度差为h,在空中的运动可视为平抛运动,轨迹如图所示,下列说法正确的有( )
A.两手榴弹在落地前瞬间重力的功率不相同
B.从投出到落地,两颗手榴弹的重力的冲量相同
C.从投出到落地,两颗手榴弹的动量变化量相同
D.从投出到落地,两颗手榴弹的动量变化率相同
BCD
当堂检测
BD
6.(多选)(2020·沈阳期末)质量m=2 kg的小物块在某一高度以v0=5 m/s的速度开始做平抛运动,若g取10 m/s2,当运动到竖直位移与水平位移相等时,对于物块( )A.此时的瞬时速度大小为5 m/sB.此时重力的瞬时功率大小为200 WC.此过程动量改变大小为10(√5-1) kg·m/sD.此过程重力的冲量大小为20 N·s
当堂检测
7.放在水平面上的物块,受到与水平方向夹角为60°,斜向上拉力F的作用,F的大小与时间t的关系和物体速度v与时间t的关系分别如图所示,根据图象提供的信息,下面判断正确的是( )
A.由图象可以求出物体的质量
B.拉力F在4秒内的冲量是8N·s
C.拉力F在4秒内的冲量是3N·s
D.物体在4秒内的动能变化是6J
B
当堂检测
8.质量为0.5 kg的小球沿光滑水平面以v1=5 m/s的速度冲向墙壁后又以v2=4 m/s的速度反向弹回,如图所示,若球跟墙的作用时间为0.05 s,则小球所受到的平均力大小为_______ N.
90
当堂检测
9.一辆轿车强行超车时,与另一辆迎面驶来的轿车相撞,两车相撞后,两车车身因相互挤压,皆缩短了0.5 m,据测算两车相撞前速率均约为30 m/s。(1)车祸中车内质量约60 kg的人受到的平均冲力是多大?(2)若此人系有安全带,安全带在车祸过程中与人体的作用时间是1 s,则这时人体受到的平均冲力为多大?
当堂检测
10.蹦极是一项刺激的极限运动,如图所示运动员将一端固定的弹性长绳绑在腰或踝关节处,从几十米高处跳下。在某次蹦极中质量为60kg的运动员在弹性绳绷紧后又经过2s人的速度减为零,假设弹性绳长为45m,重力加速度为g=10m/s2,(忽略空气阻力)下列说法正确的是( )
A.弹性绳在绷紧后2s内对运动员的平均作用力大小为2000N
B.运动员在弹性绳绷紧后动量的改变量等于弹性绳的作用力的冲量
C.运动员从开始起跳到下落到最低点的整个运动过程中重力冲量与
弹性绳作用力的冲量大小相等
D.运动员从开始起跳到下落到最低点的整个运动过程中重力冲量小
于弹性绳作用力的冲量
C
当堂检测
11.2020年10月2日,浙江队在2020年全国蹦床锦标赛女子蹦床团体决赛中获得冠军,浙江队选手王子维在比赛过程中从离绷紧的弹性网面高3.2 m处落下,弹起后离弹性网面的最大高度为5 m,已知运动员的质量为60 kg,与网面的接触时间为1.2 s,重力加速度g=10 m/s2,运动员离开网面后,网面形变完全恢复,则运动员与网面接触过程中 ( )
A.网面对运动员的冲量大小为1 080 N·s
B.网面对运动员的冲量大小为1 800 N·s
C.网面对运动员做功大小为1 080 J
D.网面对运动员做功大小为0
BD
当堂检测
Ft = mv-mv0
1. 建立“柱状”模型,柱体的横截面积为S;
2. 研究“微元”对象,Δt 时间内流体长度为v0Δt,对应的质量为m=ρSv0Δt;
3. 建立方程,应用动量定理列式计算。
流体模型
微元法
v0
Δt
m = ρSv0Δt
流体微元所受的合外力的冲量=该流体微元动量的增量, 即FΔt=ΔmΔv求解
1.高压水枪的喷口半径为 r ,射出的水流速度为 v ,水平地打在竖直墙壁上后速度变为 0 。设水的密度为 ρ ,求高速水流对墙壁的平均冲力大小是多少?
解析:沿水流的方向建立坐标系,高压水枪每个 t 时间内喷出的高速水流可以视为一个圆柱体,圆柱体的高为 h=vt ,
圆柱体的体积为 V=πr2h=πr2vt ,
圆柱体的质量为 m=ρV=ρπr2vt,
圆柱体的动量大小为 p=mv=ρπr2v2t,
因为水流打到墙壁上后速度变为零,所以水流所受的冲量为 I=-p=-ρπr2v2t,
水流所受冲力的作用时间为 t ,所以可得:Ft=I=-p=-ρπr2v2t ,F=-ρπr2v2 。
根据牛顿第三定律,高速水流对墙壁的平均冲力为 F′=-F=ρπr2v2 。
流体模型
B
2.(2019·高考全国卷Ⅰ)最近,我国为“长征九号”研制的大推力新型火箭发动机联试成功,这标志着我国重型运载火箭的研发取得突破性进展。若某次实验中该发动机向后喷射的气体速度约为3 km/s,产生的推力约为4.8×106 N,则它在1 s时间内喷射的气体质量约为( )A.1.6×102 kg B.1.6×103 kgC.1.6×105 kg D.1.6×106 kg
流体模型
3.宇宙飞船进入一个宇宙尘埃区,每前进1m,就有10个平均质量为2×10-7kg的微尘粒与飞船相撞,并附在飞船上。若尘埃微粒原来的速度不计,要保持飞船的速度10 km/s,飞船喷气产生的推力至少应维持多大?
解:设飞船速度为v,飞行时间为Δt,每前进1m附着的尘粒数为n,尘粒的平均质量为m0,则在Δt内飞船增加的质量 Δm=nm0vΔt.
据动量定理FΔt=Δmv。可知推力:
流体问题的方法归纳:
⑴微元法:取很短Δt
⑵关键:①确定Δm与Δt、液体速度、密度等关系
②确定Δm作用前后速度的变化。
③ Δt趋近零时, Δm很小,所受的重力均不计
流体模型
4. 某种气体分子束由质量m=5.4×10-26kg速度V=460m/s的分子组成,各分子都向同一方向运动,垂直地打在某平面上后又以原速率反向弹回,如分子束中每立方米的体积内有n0=1.5×1020个分子,求被分子束撞击的平面所受到的压强.
解:设在△t时间内射到 S的某平面上的气体的质量为ΔM,则:
取ΔM为研究对象,受到的合外力等于平面作用到气体上的压力F,以V方向规定为正方向,由动量定理得:-F.Δt=ΔMV-(-ΔMV),解得
平面受到的压强P为:
流体模型
5.用高压水枪清洗汽车的照片如图所示。设水枪喷出水柱截面为圆形,直径为D,水流速度为v,水柱垂直汽车表面,水柱冲击汽车后沿原方向的速度为零。高压水枪的质量为M,手持高压水枪操作,已知水的密度为ρ。下列说法正确的是 ( )
A.水柱对汽车的平均冲力为1/4ρπD2v2
B.高压水枪单位时间喷出的水的质量为1/4ρvπD2
C.高压水枪喷出水柱直径D减半时,水柱对汽车的平均冲力加倍
D.当高压水枪喷口的出水速度变为原来2倍时,压强变为原来的4倍
ABD
流体模型
6.(2018全国卷I)某游乐园入口旁有一喷泉,喷出的水柱将一质量为M的卡通玩具稳定地悬停在空中。为计算方便起见,假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出;玩具底部为平板(面积略大于S);水柱冲击到玩具底板后,在竖直方向水的速度变为零,在水平方向朝四周均匀散开。忽略空气阻力。已知水的密度为ρ,重力加速度大小为g。求:
(1)喷泉单位时间内喷出的水的质量;
(2)玩具在空中悬停时,其底面相对于喷口的高度。
流体模型
7. 如图所示,用高压水枪喷出的强力水柱冲击右侧的煤层.设水柱直径为 D,水流速度为v,方向水平,水柱垂直于煤层表面,水柱冲击煤层后水的速度为零.手持高压水枪进行操作,进入水枪的水流速度可忽略不计,已知水的密度为 p.下列说法正确的是( )
A. 高压水枪单位时间喷出的水的质量为ρπvD2
B. 高压水枪的功率为ρπD2v3/8
C. 水柱对煤层的平均冲力为ρπD2v2/4
D. 手对高压水枪的作用力水平向右
BC
流体模型
8.某游乐园有一喷泉,在水泵作用喷出竖直向上的水柱,将站在冲浪板上的玩偶模型托起,悬停在空中,这一景观可做如下简化,假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出,冲浪板底部为平板且其面积大于水柱的横截面积,保证所有水都能喷到冲浪板的底部。冲击冲浪板后,水在竖直方向的速度立即变为零,已知玩偶模型和冲浪板的总质量为M,水的密度为ρ,重力加速度大小为g,空气阻力及水的粘滞阻力均可忽略不计。
(1)计算玩偶模型在空中悬停时水对冲浪板的冲击力大小
(2)求喷泉单位时间内喷出的水的质量;
(3)求玩偶模型在空中悬停时,冲浪板的底面相对于喷口的高度。
答案 (1)Mg (2)ρv0S
流体模型
解:(1)模型静止时,据二力平衡可知:F=Mg
(2)Δt内, 喷出水的体积为:ΔV=v0SΔt
质量为:Δm=ρΔV,
单位时间内质量为:m=Δm/Δt=ρv0S
(3)设高度为h,从喷出到板底过程:
据动量定理有:F·Δt=Δp ---②
解①②得:
---①
(忽略水柱微元重力的冲量)
流体模型
9.2020年11月24日,中国用长征五号运载火箭成功发射嫦娥五号探测器,并将其送入预定轨道,运载火箭点火时向下喷气,会对地面产生冲击力。假设火箭喷气口的横截面积为S,喷出气体的速度为v(相对于地面),气体垂直射向地面后竖直速度变为零。已知气体的密度为ρ,重力加速度大小为g,则气体对地面的平均冲击力
解:以气体初速度方向为正方向
据动量定理可知FΔt=ΔP=-Δmv---①
Δt内经过S的气体质量:Δm=ρV=ρvΔtS---②
解①②得F=-ΔP/Δt=-ρSv2
根据牛顿第三定律可知:气体对地面的冲击力F'=-F=ρSv2
方向竖直向下
v
F
S
流体模型
课堂引入
这些不同的生活现象中隐藏着怎样的物理规律?
一锤下去,是“蛋碎瓦全”,还是“瓦碎蛋全”呢?
课堂引入
课堂引入
为什么鸡蛋会完好无损呢?
课堂引入
第一章 动量守恒定律
第2节 动量定理
新教材人教版 物理(选择性必修第一册)
由动能定理可知:动能的变化是由于合力做功而改变。
加速度是由物体所受的合外力产生的。
那么,动量的变化又是什么原因引起的呢?
动量的变化由速度的变化导致
速度的变化是因为有加速度
也是等于合力所做功吗?
思考与讨论:
牛顿第二定律
设置物理情景:质量为m 的物体,在合力F 的作用下,经过一段时间 Δt,速度由v 变为v′,如图所示:
由牛顿第二定律:
加速度定义:
F = ma
则有:
即:
表明动量的变化与力的作用对时间的积累效果有关。
冲量
力是产生加速度的原因,
力也称作动量变化率。
合力越大动量变化越快。
1.定义:力F 与作用时间Δt 的乘积叫作力的冲量,用字母I 表示冲量。
2.公式:
4.矢量:
5.物理意义:
3.单位:
I=F·Δt (F 为恒力)
在国际单位制中,冲量的单位是牛·秒,符号是N·s
冲量的方向由力的方向决定。
若为恒定方向的力,则冲量的方向跟这力的方向相同。
反映力的作用对时间的积累效应。
一、冲量
注意:有力作用于物体,该力一定产生冲量,
但不一定做功;力对物体做了功,一定有冲量。
过程量
6.合力的冲量计算
说明:冲量的计算要明确求哪个力的冲量,还是物体的合外力的冲量。
I = Ft 只能求恒力的冲量。
几个力的合力的冲量计算,既可以先算出各个分力的冲量后再求矢量和,又可以先算各个分力的合力再算合力的冲量。
一、冲量
例1.质量m =2kg的物体,在 =370的光滑斜面的顶端由静止滑下,已知斜面的长为s =12m,g =10m/s2,物体由斜面的顶端下滑到底端的过程中.求:
(1)物体所受各个力各自的冲量? (2)合力的冲量?
θ
G
N
IG=mgt= 40N.S
方向竖直向下
IN=N t= mgcos =32 N·s
方向垂直斜面向上
I合= mg sin t = 24N·S
方向沿斜面向下
①重力的冲量:
②支持力的冲量:
③合外力的冲量:
冲量的大小与物体的运动状态无关
合力冲量:1)I=F1t1+F2t2+····· ; 2)I 合=F合·Δt
思考1:若斜面粗糙,物体沿斜面匀速下滑,求(1)(2)?
思考2:若斜面粗糙,物体沿斜面减速下/上滑,求(1)(2)?
思考3:求各个力与合力做功,比较冲量与做功关系
冲量 功
区别 意义
公式
单位
标矢量
正负
作用效果
联系
冲量与功的比较
改变物体的动量
改变物体的动能
W=Fxcos θ
I=Ft
力在时间上的累积, 对应一段时间
在F-t图像中可以用面积表示
力在位移上累积, 对应一段位移
在F-x图像中可以用面积表示
N·S
N·m(J)
矢量
标量
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
有力作用,一定有冲量;不一定做功
有了冲量的概念,FΔt= p′ - p 其表达式也可以写成:
这表明:物体在一个过程中所受力的冲量等于它在这个过程始末的动量变化量,这个关系叫作动量定理。
I=p′-p 或者 F(t′-t)=mv′-mv
二、动量定理
1.内容:物体在一个过程中所受力的冲量等于它始末的动量变化量。
2.表达式:
①“力的冲量”是指合力的冲量,可以是恒力,可以是变力.
②表明合外力的冲量是动量变化的原因;
③ 动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同。
④动量的变化率:动量的变化跟发生这一变化所用的时间的比值。由动量定理,得 ,可见,动量的变化率等于物体所受的合力。
I=p′-p 或 FΔt = mv′-mv
3.理解:
二、动量定理
动量定理的优点:不考虑中间过程,只考虑初末状态。
三、动量定理
4.动量定理的适用范围:
①适用于恒力,也适用变力(平均值);
②可以解决匀变速直线运动,还可以解决曲线运动
③仅适用于宏观低速物体,也适用于微观现象和变速运动问题。
例题:一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间 为0.01s。球棒对垒球的平均作用力是多大?
解析:垒球的初动量为
p=mv=0.18×25 kg·m/s=4.5kg·m/s
垒球的末动量为
pˊ=mvˊ=(-0.18)×25 kg·m/s= - 8.1kg·m/s
由动量定理知垒球所受的平均作用力为
负号表示力的方向与垒球飞来的方向相反
二、动量定理
动量定理的应用步骤
1.确定研究对象:一般为单个物体;
4.选定正方向,确定在物理过程中研究对象的动量的变化;
5.根据动量定理列方程,统一单位后代入数据求解。
2.明确物理过程:受力分析,求出合外力的冲量;
3.明确研究对象的初末状态及相应的动量;
例:一个质量 m=2 kg 的物体,静止在光滑的水平地面上,某时刻受到F=10N的水平力的作用,经历t=5 s的时间。(g 为 10 m/s2)求 :
(1)重力的冲量; (2)支持力的冲量;(3)外力F的冲量;(4)合力的冲量。
解:(1)IG=Gt=100 N·s ;(2)IFN=FNt=100 N·s ;(3)IF= Ft =50 N·s 。
(4)合力的冲量。
法一:I合=IG+IFN+IF(矢量叠加)
I合=IF=50 N·s
法二:I合=F合 t
=Ft =50 N·s
法三:动量定理
I合=p′-p=mv′-mv
法一:先算出各个分力的冲量后再求矢量和。
总结:合力的冲量计算方法
法二:先算各个分力的合力再算合力的冲量。
法三:利用动量定理计算合力的冲量。
类比合力的功计算方法
(1)落地时vy2=2gh=10m/s
所以v=√v02+vy2=10√2m/s
则P=mv=10√2kgm/s,
(2)Δp=√p2-p02=10kgm/s,
例题:一个质量为 1 kg 的物体从距地面高为h=5m处以v0=10m/s的水平初速度抛出g=10m/s2.求:
(1)落地时动量
(2) 下落过程中动量的变化量
解:
(1)初末动量不共线时,动量变化只能矢量运算
(2)求动量、动量变化、冲量时,要作方向说明
与水平地面成夹角45°
方向竖直向下
例题:在撑竿跳比赛的横杆下方要放上很厚的海绵垫子.设一位撑竿跳运动员的质量为70 kg,越过横杆后从h=5.6 m高处落下,落在海绵垫上经历时间Δt=1 s停下.求海绵垫对运动员的作用力.(g=10m/s2)
解:下落到静止,以竖直向下为正方向
据动量定理可知:IG+IF=ΔP=0 ---①
自由落体过程:h=gt2/2 ---②
即:mg(t+Δt)+FΔt=0 ---③
代入数据解①②③得:F=-1441N,方向竖直向上
(1)多过程可全程立式求解
(2)动量的变化等于合力的冲量,不是某一个力的冲量
(3)多力共线时,合力冲量时可直接代数运算
将该段时间
无限分割
F
t/s
4
3
2
1
0
2
4
6
10
8
t/s
4
3
2
1
0
2
4
6
10
8
F
t/s
4
3
2
1
0
2
4
6
10
8
F
一段时间内的变力
近似认为物体在每一时段以受到某一恒力
一段时间内的变力的冲量
微分求和
由图可知F-t图线与时间轴之间所围的“面积”的大小表示对应时间t0内,力F0的冲量的大小。
微元法
思考
如果一个力随时间不断变化,又该怎样求冲量?
①变力的冲量通常可利用动量定理 I=Δp 求解
②可用图象法计算冲量。阴影部分的面积就表示力在时间Δt=t2-t1内的冲量。
③对于方向不变、大小随时间均匀变化的变力,冲量也可用I=F(t'-t)计算,但式中的F应为Δt时间内的平均力,即
微元法
变力的冲量计算方法
如何运用动量定理解释生活中的相关现象?
思考
1.跳高比赛中为什么要垫海绵垫?
2.与直接落在地面上什么相同?什么不同?
增大运动员落地减速过程的作用时间,减小冲击力
动量变化Δp相同,减速过程作用时间Δt不同,合力F合不同,冲击力F不同
1.解释有关现象
透过现象看本质——探究物理规律
越长,
一定,
越短,
则F越小.
则F越大.
一定,
例:(2018全国卷II)若一个50 g的鸡蛋从20m坠下,与地面的撞击时间约为0.001s,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102 N C.103 N D.104 N
C
思考:若地面平铺一层海绵,使得撞击时间变为0.1s,冲击力?
10N
——缓冲作用
四、动量定理的应用
2.用锤子使劲压钉子,就很难把钉子压入木块中去,如果用锤子以一定的速度敲钉子,钉子就很容易钻入木块,这是为什么?
3.1980年,一架英国的“鸽式”战斗机在威夫士地区上空与一只秃鹰相撞,飞机坠毁,飞行员弹射逃生……
小小飞禽何以能撞毁飞机这样的庞然大物?
四、动量定理的应用
1.解释有关现象
②t一定,F大则△P大,F小则△P小;
③F一定,t长则△P大,t短则△P小。
例:对于力的冲量,下列说法正确的是 ( )
A. 力越大,力的冲量就越大;
B. 作用在物体上的力大,力的冲量不一定大;
C. 力与位移垂直时,力的冲量为零;
D. 物体在水平推力作用下, 经一段时间t后仍处于静止状态,则此推力的冲量为零。
B
四、动量定理的应用
例:(2020全国卷1)行驶中的汽车如果发生剧烈碰撞,车内的安全气囊会被弹出并瞬间充满气体。若碰撞后汽车的速度在很短时间内减小为零,关于安全气囊在此过程中的作用,下列说法正确的是( )
A.增加了司机单位面积的受力大小
B.减少了碰撞前后司机动量的变化量
C.将司机的动能全部转换成汽车的动能
D.延长了司机的受力时间并增大了司机的受力面积
D
玻璃杯掉在坚硬的地面上很容易摔碎,掉在地毯上就不容易摔碎。
四、动量定理的应用
快递包装用的材料
四、动量定理的应用
消防救生气垫
船靠岸时边缘上的废旧轮胎
四、动量定理的应用
为什么鸡蛋会完好无损呢?
四、动量定理的应用
STSE
1.汽车的碰撞试验
1)汽车的安全气囊的保护作用
2)轿车前面的发动机舱并不是越坚固越好
带气垫的运动鞋
下落时屈膝
课堂小结
01
02
03
动量定理
动量定理:物体所受合外力的冲量等于物体的动量变化,这就是动量定理。
动量定理
的应用
动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同;
冲量
冲量:作用在物体上的力和作用时间的乘积,叫做该力对这个物体的冲量I
冲量是矢量,过程量,反映了力对时间的积累效应.
I=Ft
1.如图,一物体静止在水平地面上,受到与水平方向成 θ 角的恒定拉力 F 作用时间 t 后,物体仍保持静止。现有以下看法:
A.物体所受拉力 F 的冲量方向水平向右
B.物体所受拉力 F 的冲量大小是 Ft cos θ
C.物体所受摩擦力的冲量大小为 0
D.物体所受合力的冲量大小为 0
你认为这些看法正确吗?请简述你的理由。
练习与应用 P10
解析:A.错误,物体所受拉力的冲量方向与拉力方向相同;B.错误,物体所受拉力的冲量大小为 Ft ;C.错误,物体所受摩擦力的冲量大小为 Ft cos θ ;D.正确,物体静止,所以物体所受合力大小为零,物体所受合力的冲量大小为 0 。
2.体操运动员在落地时总要屈腿,这是为什么?
答:体操运动员落地时的动量是一定的,在落地过程中,动量的变化量一定。由动量定理可知,运动员受到的冲量 I 一定;由 I=Ft 可知,体操运动员在着地时屈腿可以延长作用时间 t ,可以减小运动员所受的平均冲力 F 。
练习与应用 P10
3.如图,用 0.5 kg 的铁锤钉钉子。打击前铁锤的速度为 4 m/s ,打击后铁锤的速度变为 0 ,设打击时间为 0.01 s ,g 取10 m/s2 。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,在什么情况下可
以不计铁锤所受的重力。
练习与应用 P10
解析:
(1)不考虑铁锤的重力,铁锤只受到钉子的作用力,由动量定理得:
Ft=mv,代入数据得:F=200 N 。
根据牛顿第三定律,铁锤对钉子的作用力为 F′=F=200 N ;
3.如图,用 0.5 kg 的铁锤钉钉子。打击前铁锤的速度为 4 m/s ,打击后铁锤的速度变为 0 ,设打击时间为 0.01 s ,g 取10 m/s2 。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,在什么情况下可
以不计铁锤所受的重力。
练习与应用 P10
解析:
(2)考虑铁锤的重力,对铁锤,由动量定理可得:(F-mg)t=mv,
代入数据可得:F=205 N 。
根据牛顿第三定律,铁锤对钉子的作用力 F′=F=205 N ;
3.如图,用 0.5 kg 的铁锤钉钉子。打击前铁锤的速度为 4 m/s ,打击后铁锤的速度变为 0 ,设打击时间为 0.01 s ,g 取10 m/s2 。
(1)不计铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(2)考虑铁锤所受的重力,铁锤钉钉子的平均作用力是多大?
(3)你分析一下,在计算铁锤钉钉子的平均作用力时,在什么情况下可
以不计铁锤所受的重力。
练习与应用 P10
解析:
(3)根据(1)和(2)两问铁锤对钉子的作用力可知,205 N 比 200 N 大 5 N,为 ×100%=2.4 % ,由此可知,当作用时间比较小的时候,铁锤的重力可以忽略不计。
4. 一个质量为 10 kg 的物体,以 10 m/s 的速度做直线运动,受到一个反向的作用力 F,经过 4 s,速度变为反向 2 m/s。这个力是多大?
练习与应用 P10
解析:取初速度方向为正方向,设这个理的大小为F,根据题意,由动量定理得:
解得:
5. 一个质量为 60 kg 的蹦床运动员,从离水平网面 3.2 m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0 m 高处。已知运动员与网接触的时间为 0.8 s,g 取 10 m/s2。
(1)求运动员与网接触的这段时间内动量的变化量。
(2)求网对运动员的平均作用力大小。
(3)求从自由下落开始到蹦回离水平网面5.0 m 高处这一过程中运动员所受重力的冲量、弹力的冲量。
练习与应用 P10
解析:
(1)向下接触网面的速度为:
向上离开网面的速度为:
向上为正,动量的变化量为
5. 一个质量为 60 kg 的蹦床运动员,从离水平网面 3.2 m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0 m 高处。已知运动员与网接触的时间为 0.8 s,g 取 10 m/s2。
(1)求运动员与网接触的这段时间内动量的变化量。
(2)求网对运动员的平均作用力大小。
(3)求从自由下落开始到蹦回离水平网面5.0 m 高处这一过程中运动员所受重力的冲量、弹力的冲量。
练习与应用 P10
解析:
(2)网对运动员的平均作用力为F,根据动量定理:
代入数据解得:F=1950N
5. 一个质量为 60 kg 的蹦床运动员,从离水平网面 3.2 m 高处自由下落,着网后沿竖直方向蹦回到离水平网面 5.0 m 高处。已知运动员与网接触的时间为 0.8 s,g 取 10 m/s2。
(1)求运动员与网接触的这段时间内动量的变化量。
(2)求网对运动员的平均作用力大小。
(3)求从自由下落开始到蹦回离水平网面5.0 m 高处这一过程中运动员所受重力的冲量、弹力的冲量。
练习与应用 P10
解析:(3)向下接触网面的时间为:
向上运动到最高的时间为:
重力的冲量:
弹力的冲量:
6. 曾经有一则新闻报道,一名 4 岁儿童从3 层高的楼房掉下来,被一名见义勇为的青年接住。请你估算一下,儿童受到的合力的冲量是多大?设儿童与青年之间的相互作用时间为 0.1 s,则儿童受到的合力的平均值有多大?
练习与应用 P10
解析:取向下为正方向,设儿童的质量为m= 20kg ,g =10m/s2。
第三层楼的地板离地面高为h=6m,儿童落地时的速度为v,
由v2= 2gh得,v= √2gh。
儿童被青年接住的过程中,设儿童受到的合力的冲量为I,由动量定理得:
I=0 - mv = -m√2gh≈ -219.1N S,
设儿童受到的合力的平均值为F,由动量定理得I=Ft,其中t =0.1s,
解得:F =-2191N,所以合力的平均值为2191N,方向为竖直向上。
1.(多选)关于冲量和动量,下列说法中正确的是( )
A.冲量是反映力的作用时间积累效果的物理量
B.动量是描述物体运动状态的物理量
C.冲量是物体动量变化的原因
D.冲量是描述物体状态的物理量
ABC
当堂检测
2.甲乙两个质量相同的物体,以相同的初速度分别在粗糙程度不同的水平面上运动,乙物体先停下来,甲物体又经较长时间停下来,正确的是( )
A.甲物体受到的冲量大
B.乙物体受到的冲量大
C.两个物体受到的冲量大小相等
D.无法判断
C
当堂检测
3.(多选)在任何相等的时间内,物体动量变化量相等的运动是( )
A.竖直上抛运动 B.匀速圆周运动
C.自由落体运动 D.平抛运动
ACD
当堂检测
4.(多选)(2017·高考全国卷Ⅲ)一质量为 2 kg 的物块在合外力F 的作用下从静止开始沿直线运动。F 随时间t 变化的图线如图所示,则( )A.t=1 s时物块的速率为1 m/sB.t=2 s时物块的动量大小为4 kg·m/sC.t=3 s时物块的动量大小为5 kg·m/sD.t=4 s时物块的速度为零
当堂检测
AB
5.(多选)长征途中,为了突破敌方关隘,战士爬上陡销的山头,居高临下向敌方工事内投掷手榴弹,战士在同一位置先后投出甲、乙两颗质量均为m的手榴弹,手榴弹从投出的位置到落地点的高度差为h,在空中的运动可视为平抛运动,轨迹如图所示,下列说法正确的有( )
A.两手榴弹在落地前瞬间重力的功率不相同
B.从投出到落地,两颗手榴弹的重力的冲量相同
C.从投出到落地,两颗手榴弹的动量变化量相同
D.从投出到落地,两颗手榴弹的动量变化率相同
BCD
当堂检测
BD
6.(多选)(2020·沈阳期末)质量m=2 kg的小物块在某一高度以v0=5 m/s的速度开始做平抛运动,若g取10 m/s2,当运动到竖直位移与水平位移相等时,对于物块( )A.此时的瞬时速度大小为5 m/sB.此时重力的瞬时功率大小为200 WC.此过程动量改变大小为10(√5-1) kg·m/sD.此过程重力的冲量大小为20 N·s
当堂检测
7.放在水平面上的物块,受到与水平方向夹角为60°,斜向上拉力F的作用,F的大小与时间t的关系和物体速度v与时间t的关系分别如图所示,根据图象提供的信息,下面判断正确的是( )
A.由图象可以求出物体的质量
B.拉力F在4秒内的冲量是8N·s
C.拉力F在4秒内的冲量是3N·s
D.物体在4秒内的动能变化是6J
B
当堂检测
8.质量为0.5 kg的小球沿光滑水平面以v1=5 m/s的速度冲向墙壁后又以v2=4 m/s的速度反向弹回,如图所示,若球跟墙的作用时间为0.05 s,则小球所受到的平均力大小为_______ N.
90
当堂检测
9.一辆轿车强行超车时,与另一辆迎面驶来的轿车相撞,两车相撞后,两车车身因相互挤压,皆缩短了0.5 m,据测算两车相撞前速率均约为30 m/s。(1)车祸中车内质量约60 kg的人受到的平均冲力是多大?(2)若此人系有安全带,安全带在车祸过程中与人体的作用时间是1 s,则这时人体受到的平均冲力为多大?
当堂检测
10.蹦极是一项刺激的极限运动,如图所示运动员将一端固定的弹性长绳绑在腰或踝关节处,从几十米高处跳下。在某次蹦极中质量为60kg的运动员在弹性绳绷紧后又经过2s人的速度减为零,假设弹性绳长为45m,重力加速度为g=10m/s2,(忽略空气阻力)下列说法正确的是( )
A.弹性绳在绷紧后2s内对运动员的平均作用力大小为2000N
B.运动员在弹性绳绷紧后动量的改变量等于弹性绳的作用力的冲量
C.运动员从开始起跳到下落到最低点的整个运动过程中重力冲量与
弹性绳作用力的冲量大小相等
D.运动员从开始起跳到下落到最低点的整个运动过程中重力冲量小
于弹性绳作用力的冲量
C
当堂检测
11.2020年10月2日,浙江队在2020年全国蹦床锦标赛女子蹦床团体决赛中获得冠军,浙江队选手王子维在比赛过程中从离绷紧的弹性网面高3.2 m处落下,弹起后离弹性网面的最大高度为5 m,已知运动员的质量为60 kg,与网面的接触时间为1.2 s,重力加速度g=10 m/s2,运动员离开网面后,网面形变完全恢复,则运动员与网面接触过程中 ( )
A.网面对运动员的冲量大小为1 080 N·s
B.网面对运动员的冲量大小为1 800 N·s
C.网面对运动员做功大小为1 080 J
D.网面对运动员做功大小为0
BD
当堂检测
Ft = mv-mv0
1. 建立“柱状”模型,柱体的横截面积为S;
2. 研究“微元”对象,Δt 时间内流体长度为v0Δt,对应的质量为m=ρSv0Δt;
3. 建立方程,应用动量定理列式计算。
流体模型
微元法
v0
Δt
m = ρSv0Δt
流体微元所受的合外力的冲量=该流体微元动量的增量, 即FΔt=ΔmΔv求解
1.高压水枪的喷口半径为 r ,射出的水流速度为 v ,水平地打在竖直墙壁上后速度变为 0 。设水的密度为 ρ ,求高速水流对墙壁的平均冲力大小是多少?
解析:沿水流的方向建立坐标系,高压水枪每个 t 时间内喷出的高速水流可以视为一个圆柱体,圆柱体的高为 h=vt ,
圆柱体的体积为 V=πr2h=πr2vt ,
圆柱体的质量为 m=ρV=ρπr2vt,
圆柱体的动量大小为 p=mv=ρπr2v2t,
因为水流打到墙壁上后速度变为零,所以水流所受的冲量为 I=-p=-ρπr2v2t,
水流所受冲力的作用时间为 t ,所以可得:Ft=I=-p=-ρπr2v2t ,F=-ρπr2v2 。
根据牛顿第三定律,高速水流对墙壁的平均冲力为 F′=-F=ρπr2v2 。
流体模型
B
2.(2019·高考全国卷Ⅰ)最近,我国为“长征九号”研制的大推力新型火箭发动机联试成功,这标志着我国重型运载火箭的研发取得突破性进展。若某次实验中该发动机向后喷射的气体速度约为3 km/s,产生的推力约为4.8×106 N,则它在1 s时间内喷射的气体质量约为( )A.1.6×102 kg B.1.6×103 kgC.1.6×105 kg D.1.6×106 kg
流体模型
3.宇宙飞船进入一个宇宙尘埃区,每前进1m,就有10个平均质量为2×10-7kg的微尘粒与飞船相撞,并附在飞船上。若尘埃微粒原来的速度不计,要保持飞船的速度10 km/s,飞船喷气产生的推力至少应维持多大?
解:设飞船速度为v,飞行时间为Δt,每前进1m附着的尘粒数为n,尘粒的平均质量为m0,则在Δt内飞船增加的质量 Δm=nm0vΔt.
据动量定理FΔt=Δmv。可知推力:
流体问题的方法归纳:
⑴微元法:取很短Δt
⑵关键:①确定Δm与Δt、液体速度、密度等关系
②确定Δm作用前后速度的变化。
③ Δt趋近零时, Δm很小,所受的重力均不计
流体模型
4. 某种气体分子束由质量m=5.4×10-26kg速度V=460m/s的分子组成,各分子都向同一方向运动,垂直地打在某平面上后又以原速率反向弹回,如分子束中每立方米的体积内有n0=1.5×1020个分子,求被分子束撞击的平面所受到的压强.
解:设在△t时间内射到 S的某平面上的气体的质量为ΔM,则:
取ΔM为研究对象,受到的合外力等于平面作用到气体上的压力F,以V方向规定为正方向,由动量定理得:-F.Δt=ΔMV-(-ΔMV),解得
平面受到的压强P为:
流体模型
5.用高压水枪清洗汽车的照片如图所示。设水枪喷出水柱截面为圆形,直径为D,水流速度为v,水柱垂直汽车表面,水柱冲击汽车后沿原方向的速度为零。高压水枪的质量为M,手持高压水枪操作,已知水的密度为ρ。下列说法正确的是 ( )
A.水柱对汽车的平均冲力为1/4ρπD2v2
B.高压水枪单位时间喷出的水的质量为1/4ρvπD2
C.高压水枪喷出水柱直径D减半时,水柱对汽车的平均冲力加倍
D.当高压水枪喷口的出水速度变为原来2倍时,压强变为原来的4倍
ABD
流体模型
6.(2018全国卷I)某游乐园入口旁有一喷泉,喷出的水柱将一质量为M的卡通玩具稳定地悬停在空中。为计算方便起见,假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出;玩具底部为平板(面积略大于S);水柱冲击到玩具底板后,在竖直方向水的速度变为零,在水平方向朝四周均匀散开。忽略空气阻力。已知水的密度为ρ,重力加速度大小为g。求:
(1)喷泉单位时间内喷出的水的质量;
(2)玩具在空中悬停时,其底面相对于喷口的高度。
流体模型
7. 如图所示,用高压水枪喷出的强力水柱冲击右侧的煤层.设水柱直径为 D,水流速度为v,方向水平,水柱垂直于煤层表面,水柱冲击煤层后水的速度为零.手持高压水枪进行操作,进入水枪的水流速度可忽略不计,已知水的密度为 p.下列说法正确的是( )
A. 高压水枪单位时间喷出的水的质量为ρπvD2
B. 高压水枪的功率为ρπD2v3/8
C. 水柱对煤层的平均冲力为ρπD2v2/4
D. 手对高压水枪的作用力水平向右
BC
流体模型
8.某游乐园有一喷泉,在水泵作用喷出竖直向上的水柱,将站在冲浪板上的玩偶模型托起,悬停在空中,这一景观可做如下简化,假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出,冲浪板底部为平板且其面积大于水柱的横截面积,保证所有水都能喷到冲浪板的底部。冲击冲浪板后,水在竖直方向的速度立即变为零,已知玩偶模型和冲浪板的总质量为M,水的密度为ρ,重力加速度大小为g,空气阻力及水的粘滞阻力均可忽略不计。
(1)计算玩偶模型在空中悬停时水对冲浪板的冲击力大小
(2)求喷泉单位时间内喷出的水的质量;
(3)求玩偶模型在空中悬停时,冲浪板的底面相对于喷口的高度。
答案 (1)Mg (2)ρv0S
流体模型
解:(1)模型静止时,据二力平衡可知:F=Mg
(2)Δt内, 喷出水的体积为:ΔV=v0SΔt
质量为:Δm=ρΔV,
单位时间内质量为:m=Δm/Δt=ρv0S
(3)设高度为h,从喷出到板底过程:
据动量定理有:F·Δt=Δp ---②
解①②得:
---①
(忽略水柱微元重力的冲量)
流体模型
9.2020年11月24日,中国用长征五号运载火箭成功发射嫦娥五号探测器,并将其送入预定轨道,运载火箭点火时向下喷气,会对地面产生冲击力。假设火箭喷气口的横截面积为S,喷出气体的速度为v(相对于地面),气体垂直射向地面后竖直速度变为零。已知气体的密度为ρ,重力加速度大小为g,则气体对地面的平均冲击力
解:以气体初速度方向为正方向
据动量定理可知FΔt=ΔP=-Δmv---①
Δt内经过S的气体质量:Δm=ρV=ρvΔtS---②
解①②得F=-ΔP/Δt=-ρSv2
根据牛顿第三定律可知:气体对地面的冲击力F'=-F=ρSv2
方向竖直向下
v
F
S
流体模型
