人教版七年级下册5.3.1平行线的性质课件(共16张PPT)
文档属性
| 名称 | 人教版七年级下册5.3.1平行线的性质课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 544.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
2
1
2
1
c
a
b
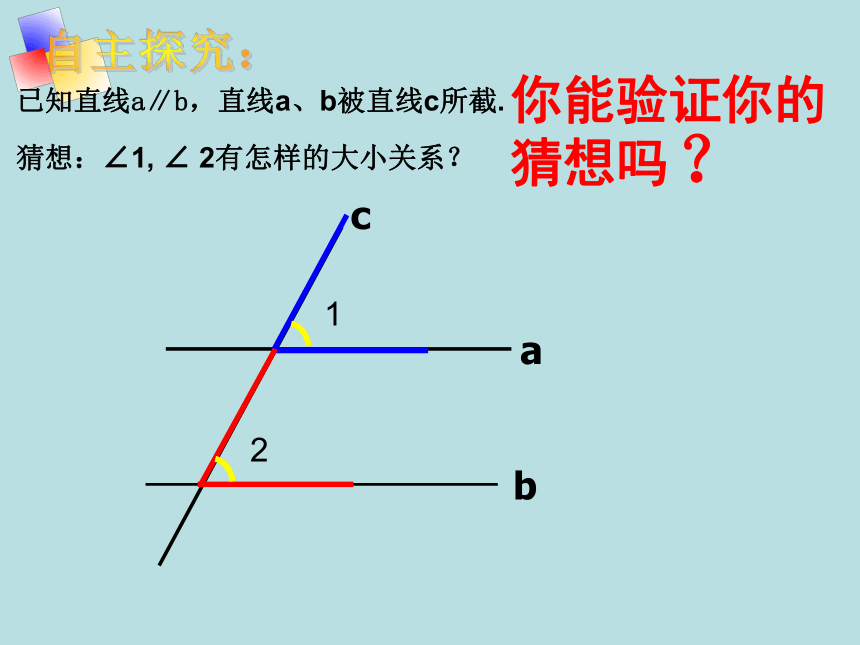
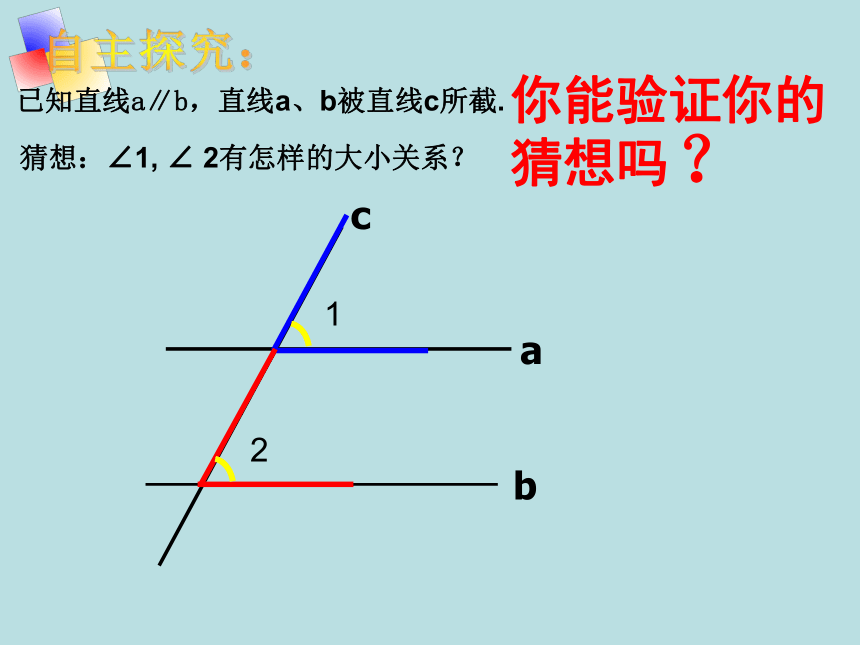
已知直线a∥b,直线a、b被直线c所截.
a
b
c
1
2
猜想:∠1, ∠ 2有怎样的大小关系?
你能验证你的猜想吗
?
已知直线a∥b,直线a、b被直线c所截.
a
b
c
猜想:∠1, ∠ 2有怎样的大小关系?
1
2
你能验证你的猜想吗
?
两条平行线被第三条直线所截,同位角相等。那么其内错角、同旁内角分别又有什么关系呢?
解: ∠ 2 = ∠3 理由如下:
∵ a∥b,
∴ ∠1= ∠2( )
又 ∵ ∠3 = ∠ 1 (对顶角相等),
∴ ∠ 2 = ∠3.
1
2
3
a
b
(1)如图,已知:a// b
那么 3与 2有什么关系?
(2)如图:已知a//b,
那么 2与 4有什么关系呢?
4
简要说明
解: 2 + 4=180° 理由如下:
∵ a//b (已知)
∴ 1= 2( )
∵ 1+ 4=180°(邻补角定义)
∴ 2+ 4=180°(等量代换)
两直线平行,同位角相等
两直线平行,同位角相等
2╭
╯1
A
E
D
B
C
4 (
╯3
如图,已知平行线AB、CD被直线AE所截 , ∠1=110 ゜ ,那么
∠2=—— ;∠3=——;∠4=——
110°
110°
70°
应用举例
如图是梯形铁片有上底的残余部分,已经量得∠A=100°, ∠B=115°,那么梯形的另外两个角各是多少度?
解:∵因为梯形的上下两底互相平行
∴ ∠A+∠D= 180° ,
∠B+∠C= 180° (两直线平行,同旁内角互补)
∴ ∠D=180°-100°=80°,
∠C=180°- 115°= 65°
故梯形的另外两个角分别是80°和65°.
B
C
A
D
运用下图,请你和小组成员一起合作编一道应用平行线性质的题,老师将选出最有创意的小组作品在全班进行展示.
B
A
C
D
E
F
对自己说我有哪些收获?
对同学有哪些温馨提示?
对老师说你还有那些困惑?
还想进一步研究那些知识?
……
1、平行线的三个性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
a
b
c
2、①几何结论的得出需要大胆的猜想多形式的验证
(度量法、叠合法、几何推理法).
②体会了转化的数学思想。
在校园里去寻找能体现平行线性质应用的实际例子,并讲给你的同桌听。
2
1
2
1
c
a
b
已知直线a∥b,直线a、b被直线c所截.
a
b
c
1
2
猜想:∠1, ∠ 2有怎样的大小关系?
你能验证你的猜想吗
?
已知直线a∥b,直线a、b被直线c所截.
a
b
c
猜想:∠1, ∠ 2有怎样的大小关系?
1
2
你能验证你的猜想吗
?
两条平行线被第三条直线所截,同位角相等。那么其内错角、同旁内角分别又有什么关系呢?
解: ∠ 2 = ∠3 理由如下:
∵ a∥b,
∴ ∠1= ∠2( )
又 ∵ ∠3 = ∠ 1 (对顶角相等),
∴ ∠ 2 = ∠3.
1
2
3
a
b
(1)如图,已知:a// b
那么 3与 2有什么关系?
(2)如图:已知a//b,
那么 2与 4有什么关系呢?
4
简要说明
解: 2 + 4=180° 理由如下:
∵ a//b (已知)
∴ 1= 2( )
∵ 1+ 4=180°(邻补角定义)
∴ 2+ 4=180°(等量代换)
两直线平行,同位角相等
两直线平行,同位角相等
2╭
╯1
A
E
D
B
C
4 (
╯3
如图,已知平行线AB、CD被直线AE所截 , ∠1=110 ゜ ,那么
∠2=—— ;∠3=——;∠4=——
110°
110°
70°
应用举例
如图是梯形铁片有上底的残余部分,已经量得∠A=100°, ∠B=115°,那么梯形的另外两个角各是多少度?
解:∵因为梯形的上下两底互相平行
∴ ∠A+∠D= 180° ,
∠B+∠C= 180° (两直线平行,同旁内角互补)
∴ ∠D=180°-100°=80°,
∠C=180°- 115°= 65°
故梯形的另外两个角分别是80°和65°.
B
C
A
D
运用下图,请你和小组成员一起合作编一道应用平行线性质的题,老师将选出最有创意的小组作品在全班进行展示.
B
A
C
D
E
F
对自己说我有哪些收获?
对同学有哪些温馨提示?
对老师说你还有那些困惑?
还想进一步研究那些知识?
……
1、平行线的三个性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
a
b
c
2、①几何结论的得出需要大胆的猜想多形式的验证
(度量法、叠合法、几何推理法).
②体会了转化的数学思想。
在校园里去寻找能体现平行线性质应用的实际例子,并讲给你的同桌听。
