北师大版数学七下 4.1认识三角形(1)学案(无答案)
文档属性
| 名称 | 北师大版数学七下 4.1认识三角形(1)学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 61.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览

文档简介
第四章 三角形
4.1认识三角形(1)
【学习目标】1.认识三角形,能用符号语言表示三角形,并把三角形分类;2. 能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”; 3.能按角将三角形分类;
【学习重点】:三角形内角和定理推理和应用。
【学习难点】:三角形内角和定理推理和应用。
【学习过程】:
一、预学:
1、提出问题,创设情境
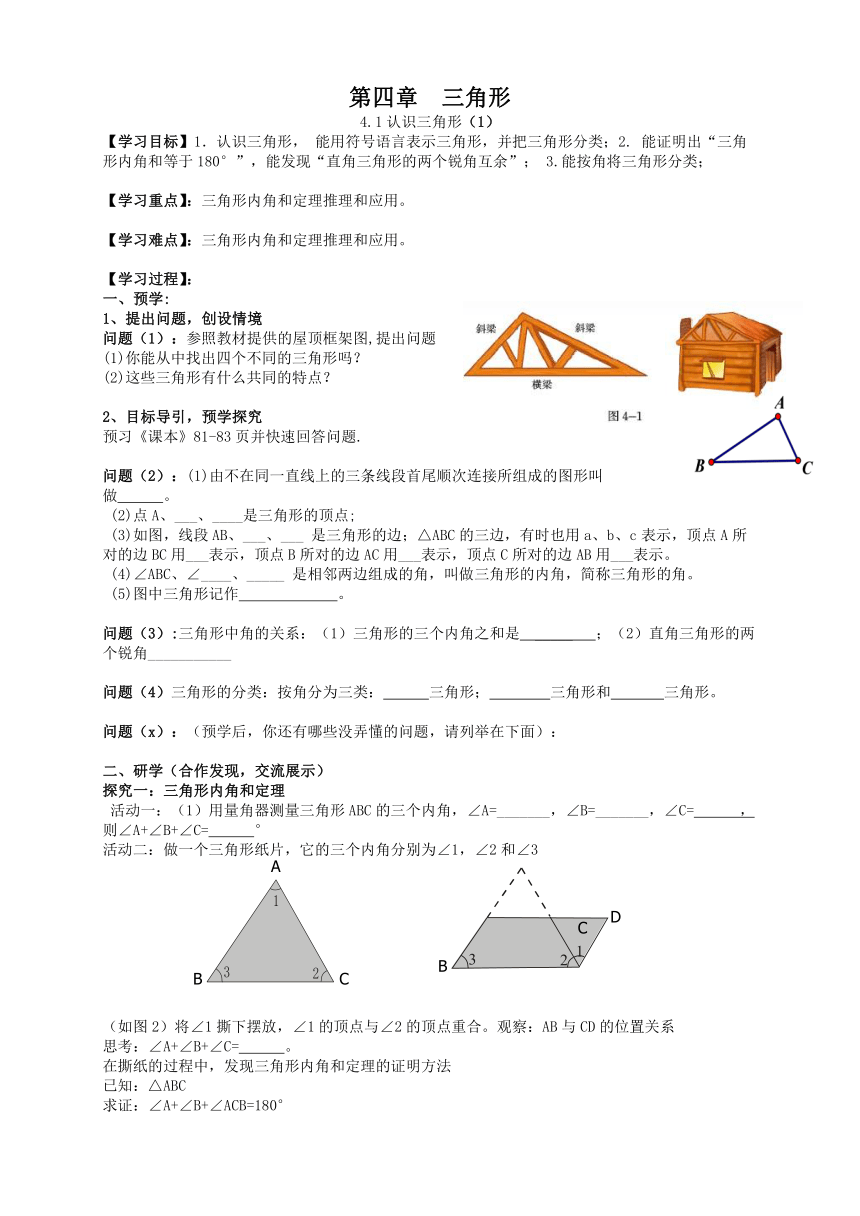
问题(1):参照教材提供的屋顶框架图,提出问题 (1)你能从中找出四个不同的三角形吗?
(2)这些三角形有什么共同的特点?
2、目标导引,预学探究
预习《课本》81-83页并快速回答问题.
问题(2):(1)由不在同一直线上的三条线段首尾顺次连接所组成的图形叫做 。
(2)点A、___、____是三角形的顶点;
(3)如图,线段AB、___、___ 是三角形的边;△ABC的三边,有时也用a、b、c表示,顶点A所对的边BC用___表示,顶点B所对的边AC用___表示,顶点C所对的边AB用___表示。
(4)∠ABC、∠____、_____ 是相邻两边组成的角,叫做三角形的内角,简称三角形的角。
(5)图中三角形记作 。
问题(3):三角形中角的关系:(1)三角形的三个内角之和是 _____ ;(2)直角三角形的两个锐角___________
问题(4)三角形的分类:按角分为三类: 三角形; 三角形和 三角形。
问题(x):(预学后,你还有哪些没弄懂的问题,请列举在下面):
二、研学(合作发现,交流展示)
探究一:三角形内角和定理
活动一:(1)用量角器测量三角形ABC的三个内角,∠A=_______,∠B=_______,∠C= ,则∠A+∠B+∠C= °
(
A
)活动二:做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3
(
D
) (
B
2
2
A
1
3
2
)
(
C
)
图1 图2
(
B
)
(
C
) (
B
)
(如图2)将∠1撕下摆放,∠1的顶点与∠2的顶点重合。观察:AB与CD的位置关系 思考:∠A+∠B+∠C= 。
在撕纸的过程中,发现三角形内角和定理的证明方法
已知:△ABC
求证:∠A+∠B+∠ACB=180°
(
注意:原图中没有的线,因为解题的需要而添加,这样的线我们叫做辅助线。我们规定辅助线画为虚线。
过
C
作
CE
∥
AB
就是本题辅助线的作法,在证明中,它可以作理论依
据。
)证明:过C作AB的平行线CE
∵ CE∥AB(辅助线的作法)
∴ ∠A ∠ACE(两直线平行,内错角相等)
又∵ AB∥CE
∴ ∠B+∠BCE= (两直线平行,同旁内角互补)
∴ ∠A+∠B+∠ACB=180°
你还有其它的证明方法吗?
定理:三角形的内角和为180°
几何表示:在△ABC中,∠A+∠B+∠C= 。
探究二:直角三角形的性质
如右图,已知AB⊥BC直角三角形ABC记作________________,读作“Rt三角形ABC”。
它的斜边是_______,直角边是______________。思考∠A+∠C=_______.
定理:直角三角形两个锐角互余
探究三:三角形的分类
1、自学课本82页“议一议”部分回答下列问题
(1)下面的图(1)、图(2)、图(3)中的三角形被遮住的两个内角是什么角?试着说明理由.
(2)将图(3)的结果与图(1)、图(2)的结果进行比较,可以将三角形如何按角分类?
得出结论:三角形按角分为三类:(1)锐角三角形 (2)直角三角形 (3)钝角三角形
2、完成课本83页想一想
3、完成课本83-84页随堂练习
探究x:在△ABC中(1)=
(2)若=54°,,那么= ,= ____
三、评学
1、积累巩固:完成课本84页习题4.1
2、拓展延伸:
(1)图3中有几个三角形?用符号表示这些三角形.
(2)在△ABC中 (1)若∠A=45°,∠B=30°,则∠C= .
变式1:在△ ABC中,∠A=45°,∠B= 2∠C,求∠B、 ∠C的度数。
变式2:在△ ABC中,∠A=∠B= 2∠C,求∠B、 ∠C的度数。
变式3:在△ ABC中,∠A+ ∠B = ∠C ,求∠C的度数。
(3)、如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,此三角形按角分类应为__________
[课堂小结]:
通过本课学习,你掌握了那些知识?获得了哪些技能?还存在什么疑问?
4.1认识三角形(1)
【学习目标】1.认识三角形,能用符号语言表示三角形,并把三角形分类;2. 能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”; 3.能按角将三角形分类;
【学习重点】:三角形内角和定理推理和应用。
【学习难点】:三角形内角和定理推理和应用。
【学习过程】:
一、预学:
1、提出问题,创设情境
问题(1):参照教材提供的屋顶框架图,提出问题 (1)你能从中找出四个不同的三角形吗?
(2)这些三角形有什么共同的特点?
2、目标导引,预学探究
预习《课本》81-83页并快速回答问题.
问题(2):(1)由不在同一直线上的三条线段首尾顺次连接所组成的图形叫做 。
(2)点A、___、____是三角形的顶点;
(3)如图,线段AB、___、___ 是三角形的边;△ABC的三边,有时也用a、b、c表示,顶点A所对的边BC用___表示,顶点B所对的边AC用___表示,顶点C所对的边AB用___表示。
(4)∠ABC、∠____、_____ 是相邻两边组成的角,叫做三角形的内角,简称三角形的角。
(5)图中三角形记作 。
问题(3):三角形中角的关系:(1)三角形的三个内角之和是 _____ ;(2)直角三角形的两个锐角___________
问题(4)三角形的分类:按角分为三类: 三角形; 三角形和 三角形。
问题(x):(预学后,你还有哪些没弄懂的问题,请列举在下面):
二、研学(合作发现,交流展示)
探究一:三角形内角和定理
活动一:(1)用量角器测量三角形ABC的三个内角,∠A=_______,∠B=_______,∠C= ,则∠A+∠B+∠C= °
(
A
)活动二:做一个三角形纸片,它的三个内角分别为∠1,∠2和∠3
(
D
) (
B
2
2
A
1
3
2
)
(
C
)
图1 图2
(
B
)
(
C
) (
B
)
(如图2)将∠1撕下摆放,∠1的顶点与∠2的顶点重合。观察:AB与CD的位置关系 思考:∠A+∠B+∠C= 。
在撕纸的过程中,发现三角形内角和定理的证明方法
已知:△ABC
求证:∠A+∠B+∠ACB=180°
(
注意:原图中没有的线,因为解题的需要而添加,这样的线我们叫做辅助线。我们规定辅助线画为虚线。
过
C
作
CE
∥
AB
就是本题辅助线的作法,在证明中,它可以作理论依
据。
)证明:过C作AB的平行线CE
∵ CE∥AB(辅助线的作法)
∴ ∠A ∠ACE(两直线平行,内错角相等)
又∵ AB∥CE
∴ ∠B+∠BCE= (两直线平行,同旁内角互补)
∴ ∠A+∠B+∠ACB=180°
你还有其它的证明方法吗?
定理:三角形的内角和为180°
几何表示:在△ABC中,∠A+∠B+∠C= 。
探究二:直角三角形的性质
如右图,已知AB⊥BC直角三角形ABC记作________________,读作“Rt三角形ABC”。
它的斜边是_______,直角边是______________。思考∠A+∠C=_______.
定理:直角三角形两个锐角互余
探究三:三角形的分类
1、自学课本82页“议一议”部分回答下列问题
(1)下面的图(1)、图(2)、图(3)中的三角形被遮住的两个内角是什么角?试着说明理由.
(2)将图(3)的结果与图(1)、图(2)的结果进行比较,可以将三角形如何按角分类?
得出结论:三角形按角分为三类:(1)锐角三角形 (2)直角三角形 (3)钝角三角形
2、完成课本83页想一想
3、完成课本83-84页随堂练习
探究x:在△ABC中(1)=
(2)若=54°,,那么= ,= ____
三、评学
1、积累巩固:完成课本84页习题4.1
2、拓展延伸:
(1)图3中有几个三角形?用符号表示这些三角形.
(2)在△ABC中 (1)若∠A=45°,∠B=30°,则∠C= .
变式1:在△ ABC中,∠A=45°,∠B= 2∠C,求∠B、 ∠C的度数。
变式2:在△ ABC中,∠A=∠B= 2∠C,求∠B、 ∠C的度数。
变式3:在△ ABC中,∠A+ ∠B = ∠C ,求∠C的度数。
(3)、如果△ABC中,∠A∶∠B∶∠C=2∶3∶5,此三角形按角分类应为__________
[课堂小结]:
通过本课学习,你掌握了那些知识?获得了哪些技能?还存在什么疑问?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
