人教版七数学年级下册8.2 代入消元法解二元一次方程组 课件(共18张PPT)
文档属性
| 名称 | 人教版七数学年级下册8.2 代入消元法解二元一次方程组 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 22:12:51 | ||
图片预览




文档简介
(共18张PPT)
消元
——用代入法解二元一次方程组
(第1课时)
问题1:什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
问题4:什么是二元一次方程组的解?
问题2:什么是二元一次方程组?
含有两个未知数,每个未知数的项的次数都是1,并且一共
有两个方程,像这样的方程组叫做二元一次方程组.
二元一次方程组的两个方程的公共解,叫做二元
一次方程组的解。
回顾与思考
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
问题3:什么是二元一次方程的解?
1. 把下列方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式
(1)
(1)
(2)
3.如何解这样的方程组
.
.
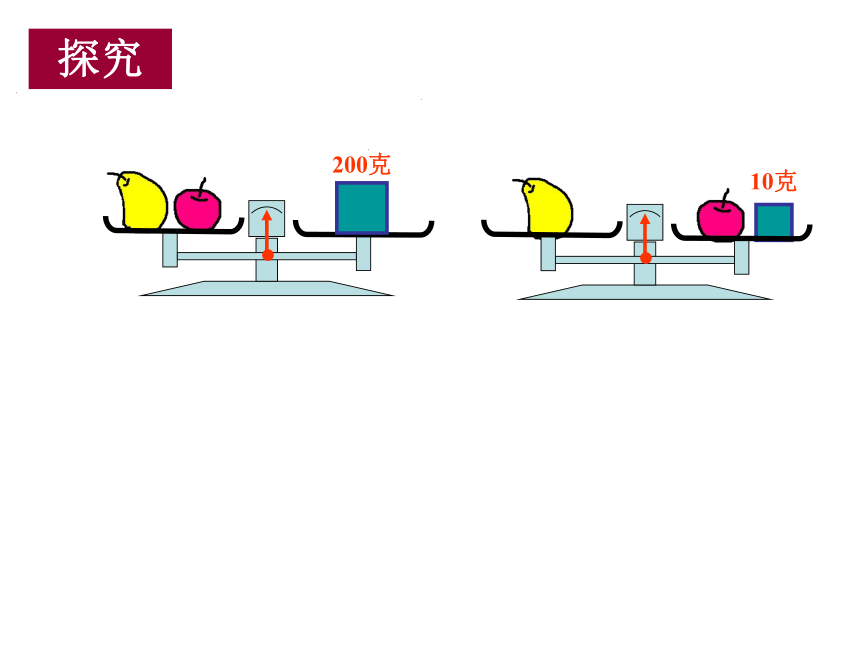
200克
10克
探究
y克
.
.
x克
200克
y克
x克
10克
x + y = 200
y = x + 10
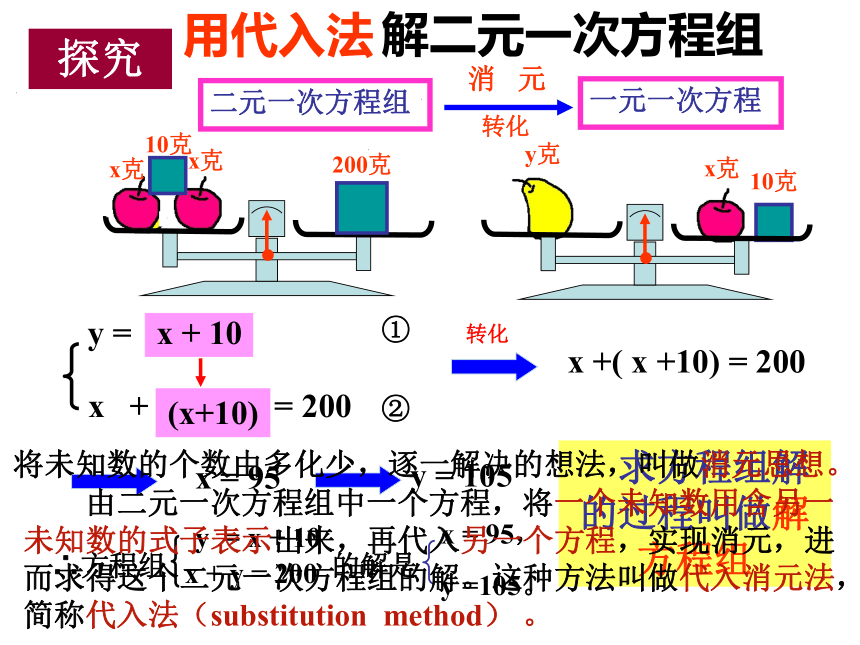
解二元一次方程组
一元一次方程
二元一次方程组
消 元
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105。
求方程组解的过程叫做解方程组
转化
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
由二元一次方程组中一个方程,将一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法(substitution method) 。
转化
探究
分析
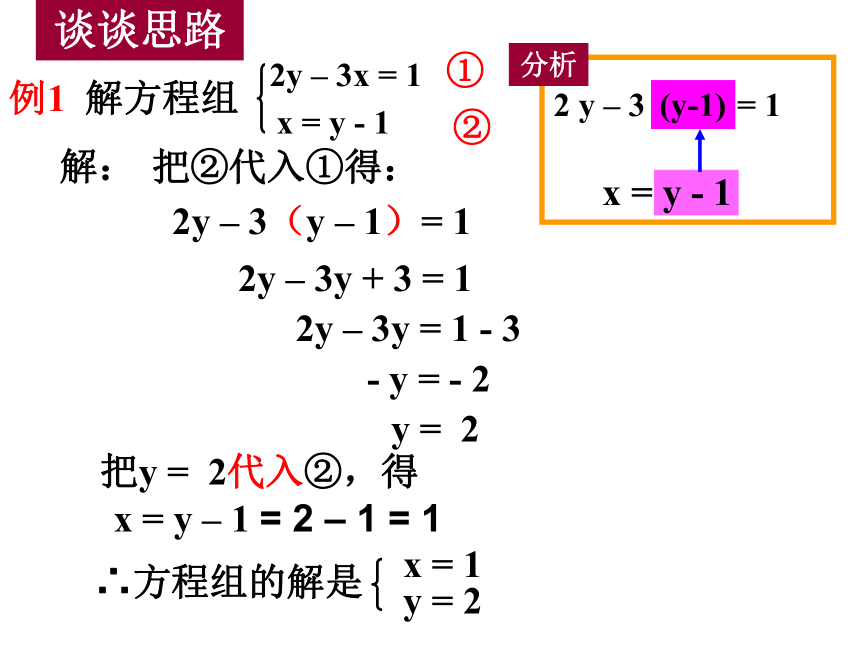
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
变:
2y – 3x = 1
x – y = – 1
①
②
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
谈谈思路
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 3+(-1)=2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法
用代入法解二元一次方程组
⑴
y=2x-3
3x+2y=8
⑵
2x- y=5
3x +4y=2
练一练(P93)
解:把② 代入①得,
3x+2(2x-3)= 8
解得,x= 2
把x = 2 代入②得
y=2×2-3= 1
∴原方程组的解为
x= 2
⑴
y=2x-3
3x+2y=8
②
①
y=1
①
②
解:由①得,
y=2x-5③
∴原方程组的解为
把③代入②得,
3x+4(2x-5)=2
解得,x=2
把x=2代入③得,
y=2×2-5=-1
⑵
2x- y=5
3x +4y=2
y=-1
x=2
m+4n=7 , ①
2m-n=5 . ②
解:由②,得 n= 2m-5 .③
把 ③代入①,得
m+4 (2m-5)=7.
解这个方程,得
m=3.
把m=3代入③,得
n= 1.
m=3,
n= 1.
所以这个方程组的解为
比一比
用代入法解方程组:
解:由① ,得 m= 7-4n .③
把 ③代入②,得
2(7-4n)-n=5.
解这个方程 ,得
n= 1.
把n=1代入③,得
m=3.
所以这个方程组的解为
m=3,
n= 1.
抢答: 请举手
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
2x+5y=21
x +3y=8
能力检测
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣=0,
求 x 、y的 值.
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
1
1
1、若方程5x m-2n+4y 3n-m = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
由题意知,
m - 2n = 1
3n – m = 1
①
②
由①得:
把③代入②得:
m = 1 +2n
③
3n –(1 + 2n)= 1
3n – 1 – 2n = 1
3n-2n = 1+1
n = 2
把n =2 代入③,得:
m = 1 +2n
能力检测
m =5
n=2
即m 的值是5,n 的值是4.
所以原方程组的解:
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
由题意知,
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
由①得:
y = 2 – 3x
把③代入得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y= 2 - 3×2
y= -4
∴
x = 2
y = -4
即x 的值是2,y 的值是-4.
能力检测
所以原方程组的解:
你有什么收获?
你还有什么困惑?
反思小结 体验收获
知识反馈 布置作业
1、必做题:
书本P97习题8.2 第1题、第2题;
2、 选做题:
友情提示:
作业整洁
字体工整
步骤完整
若方程组 的解中x、y的值
相等,求k的值
消元
——用代入法解二元一次方程组
(第1课时)
问题1:什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程。
问题4:什么是二元一次方程组的解?
问题2:什么是二元一次方程组?
含有两个未知数,每个未知数的项的次数都是1,并且一共
有两个方程,像这样的方程组叫做二元一次方程组.
二元一次方程组的两个方程的公共解,叫做二元
一次方程组的解。
回顾与思考
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
问题3:什么是二元一次方程的解?
1. 把下列方程写成用含x的式子表示y的形式.
(2)
课前热身
2.你能把上面两个方程写成用含y的式子表示x的形式
(1)
(1)
(2)
3.如何解这样的方程组
.
.
200克
10克
探究
y克
.
.
x克
200克
y克
x克
10克
x + y = 200
y = x + 10
解二元一次方程组
一元一次方程
二元一次方程组
消 元
用代入法
x克
10克
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105。
求方程组解的过程叫做解方程组
转化
将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
由二元一次方程组中一个方程,将一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法(substitution method) 。
转化
探究
分析
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
变:
2y – 3x = 1
x – y = – 1
①
②
解:
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
谈谈思路
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 3+(-1)=2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法
用代入法解二元一次方程组
⑴
y=2x-3
3x+2y=8
⑵
2x- y=5
3x +4y=2
练一练(P93)
解:把② 代入①得,
3x+2(2x-3)= 8
解得,x= 2
把x = 2 代入②得
y=2×2-3= 1
∴原方程组的解为
x= 2
⑴
y=2x-3
3x+2y=8
②
①
y=1
①
②
解:由①得,
y=2x-5③
∴原方程组的解为
把③代入②得,
3x+4(2x-5)=2
解得,x=2
把x=2代入③得,
y=2×2-5=-1
⑵
2x- y=5
3x +4y=2
y=-1
x=2
m+4n=7 , ①
2m-n=5 . ②
解:由②,得 n= 2m-5 .③
把 ③代入①,得
m+4 (2m-5)=7.
解这个方程,得
m=3.
把m=3代入③,得
n= 1.
m=3,
n= 1.
所以这个方程组的解为
比一比
用代入法解方程组:
解:由① ,得 m= 7-4n .③
把 ③代入②,得
2(7-4n)-n=5.
解这个方程 ,得
n= 1.
把n=1代入③,得
m=3.
所以这个方程组的解为
m=3,
n= 1.
抢答: 请举手
1.方程-x+4y=-15用含y的代数式表示x为( )
A.-x=4y-15 B.x=-15+4y
C. x=4y+15 D.x=-4y+15
C
B
3.用代入法解方程组 较为简便的方法是( )
A.先把①变形
B.先把②变形
C.可先把①变形,也可先把②变形
D.把①、②同时变形
B
2.将y=-2x-4代入3x-y=5可得( )
A.3x-(2x+4)=5 B. 3x-(-2x-4)=5
C.3x+2x-4=5 D. 3x-2x+4=5
2x+5y=21
x +3y=8
能力检测
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣=0,
求 x 、y的 值.
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
1
1
1、若方程5x m-2n+4y 3n-m = 9是关于x、y的二元一次方程,求m 、n 的值.
解:
由题意知,
m - 2n = 1
3n – m = 1
①
②
由①得:
把③代入②得:
m = 1 +2n
③
3n –(1 + 2n)= 1
3n – 1 – 2n = 1
3n-2n = 1+1
n = 2
把n =2 代入③,得:
m = 1 +2n
能力检测
m =5
n=2
即m 的值是5,n 的值是4.
所以原方程组的解:
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
解:
由题意知,
y + 3x – 2 = 0
5x + 2y – 2 = 0
①
②
由①得:
y = 2 – 3x
把③代入得:
③
5x + 2(2 – 3x)- 2 = 0
5x + 4 – 6x – 2 = 0
5x – 6x = 2 - 4
-x = -2
x = 2
把x = 2 代入③,得:
y= 2 - 3×2
y= -4
∴
x = 2
y = -4
即x 的值是2,y 的值是-4.
能力检测
所以原方程组的解:
你有什么收获?
你还有什么困惑?
反思小结 体验收获
知识反馈 布置作业
1、必做题:
书本P97习题8.2 第1题、第2题;
2、 选做题:
友情提示:
作业整洁
字体工整
步骤完整
若方程组 的解中x、y的值
相等,求k的值
