2021-2022学年六年级下学期数学第七单元总复习第3课时运算律及简算课件(共37张PPT)
文档属性
| 名称 | 2021-2022学年六年级下学期数学第七单元总复习第3课时运算律及简算课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 728.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 06:30:50 | ||
图片预览











文档简介
(共37张PPT)
运算律与简便运算总复习
练习巩固
探本溯源,深入理解
知识梳理,形成网络
计算对比,回顾方法
梳理总结,提升认知
当堂检测
学习任务一:计算对比,回顾方法
①:18.93-7.2-2.8=
③1.67×37+0.33×37
②: 7.36-2.36×3=
④:
1
5
÷
6
25
-
2
7
×
7
32
赛一赛:从这四道题中选择两道题做一做,看谁算得又对又快。
你选择了哪两道?为什么?
评价标准
1.算式正确。1分2.结果正确。1分
3.方法适当。1分
4.有条理、清晰的表 达自己的解题思路。1分
应用运算律可以使计算简便。
这些运算律在整数、小数、分数范围内都适用。
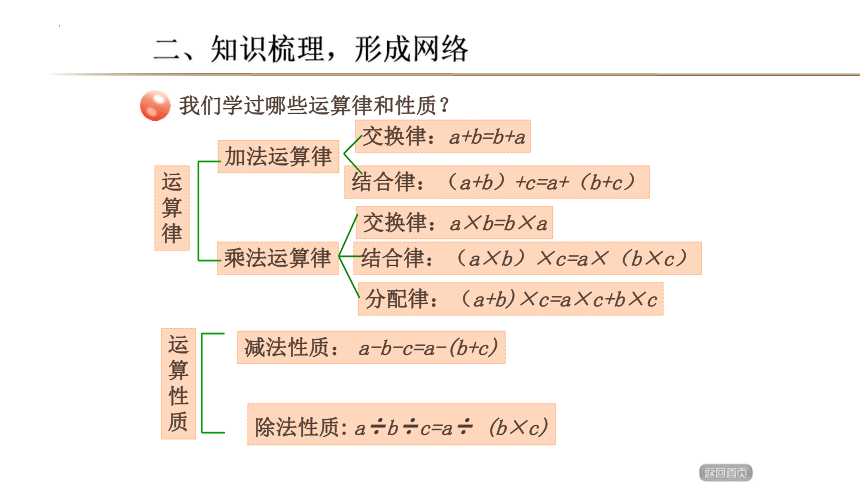
我们学过哪些运算律和性质?
二、知识梳理,形成网络
自主整理提纲:
(1)小学阶段学过哪些简便运算律和一些运算性质?
(2)你能按类别有序地、完整地把这些运算定律和运算性质整理好
整理好的同学思考:
在这些运算定律和性质中,最容易“骗”你的是哪种?该注意什么?
评价标准:1知识点梳理系统完整,书写工整,找出并说明易错点。3分
2知识点梳理系统完整,书写工整,图文结合,找出易错点语言表达条理清晰。5分
我们学过哪些运算律和性质?
加法运算律
乘法运算律
运
算
律
交换律:a+b=b+a
交换律:a×b=b×a
结合律:(a+b)+c=a+(b+c)
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
二、知识梳理,形成网络
运
算
性
质
减法性质: a-b-c=a-(b+c)
除法性质: a÷b÷c=a÷ (b×c)
易错简便运算练习要求:
1:先计算各题,怎样算简便就怎样算。写出主要运算步骤。步骤正确1分
2:想一想,对每道题的运算,你改变了什么?你的依据是什么?把你的想法写出来。条理清晰,方法正确1分
3:最后思考,在简便运算中,怎样变是好的变?2分
(1)
(2)
(3)
(4)
(5)
三、探本溯源,深入理解
改变了( )
运算顺序
(1)
= 6
三、探本溯源,深入理解
改变了( )
运算顺序、数值类型
(2)
=
= 6.25
三、探本溯源,深入理解
改变了( )
运算顺序、运算方法
(3) 13.4÷4÷2.5
= 13.4÷(4 × 2.5)
= 1.34
三、探本溯源,深入理解
改变了( )
数值的大小
(4)28÷3.5
28÷3.5
= 56÷7
= 28÷7×2
= 8
= 8
三、探本溯源,深入理解
改变了( )
数值的大小
(5) 435+199
= 435+200-1
= 634
三、探本溯源,深入理解
归纳:
评价标准:1.特点描述准确。1分2.条理清楚的说出什么改变,什么不变。计算方法。2分
1、简便运算中一般有哪几种“变”?
2、为什么要去“变”?
3、“不变”的是什么?
三、探本溯源,深入理解
依据是什么?
依据是( )
乘法结合律、乘法交换律
(1)
三、探本溯源,深入理解
依据是什么?
依据是( )
乘法分配律
(2)
=
三、探本溯源,深入理解
依据是什么?
依据是( )
除法的性质
(3) 13.4÷4÷2.5
= 13.4÷(4 × 2.5)
三、探本溯源,深入理解
依据是什么?
依据是( )
商不变的性质
(4)28÷3.5
= 56÷7
28÷3.5
= 28÷7×2
依据是( )
商的变化规律
三、探本溯源,深入理解
依据是什么?
依据是( )
和的变化规律
(5) 435+199
= 435+200-1
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
166+98=166+100 ( )
一个加数不变,另一个加数增加几,和就会( )。
要使计算结果不变,和必须要( )
2
增加几
减少几
和的变化规律
-
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
146-98=146-100 ( )
被减数不变,减数增加几,差就会( )。
要使计算结果不变,差必须要( )
2
减少几
增加几
差的变化规律
+
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
34×0.5=34×1 ( )
一个因数不变,另一个因数扩大几倍,积就会( )。
要使计算结果不变,积必须要( )
2
扩大相同的倍数
缩小相同的倍数
积的变化规律
÷
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
34÷0.5=34÷1 ( )
被除数不变,除数扩大几倍,商就会( )。
要使计算结果不变,商必须要( )
2
缩小相同的倍数
扩大相同的倍数
商的变化规律
×
三、探本溯源,深入理解
(1). 25×48=25×(40+8)
=25×40+25×8=1000+200=120
应用了( )。
(2)25×48=25×(6×8)=6×(25×8)
=6×200=1200
应用了( )。
(3)25×48=25×(50-2)
=25×50-25×2=1250-50=1200
应用了( )。
1、25×48的几种计算方法,分别应用了哪个运算定律?
乘法分配律
乘法结合律
乘法分配律
四、(1)基础练习,巩固新知
2.计算下列各题,能简算的要简算。评价标准:计算正确简便方法合理.5分一题
四、(1)基础练习,巩固新知
2000-197
8.8-6.75+9.2-0.25
41×102
0.8×3.6-0.8×0.6
=
2000-200+3
=
1800+3
=
1803
=
(8.8+9.2)
-
(6.75+0.25)
=
18
-
7
=
11
=
41×(100+2)
=
41×100+41×2
=
4100+82
=
4182
=
0.8×(3.6-0.6)
=
0.8×3
=
2.4
2.计算下列各题,能简算的要简算。
=
=
=
=
=
=
1
5
÷
6
25
-
2
7
×
7
32
7
12
+
3
8
-
23
24
×
(
)
24
1
5
×
25
6
-
2
7
×
7
32
1
5
1
1
16
1
1
16
5
6
-
14+9-23
0
3
48
40
48
-
=
37
48
-
23
24
×
24
7
12
24
×
+
3
8
24
×
四、(1)基础练习,巩固新知
2.计算下列各题,能简算的要简算。
1042-384÷16×13
4.86×[1÷(2.1-2.09)]
=
1042-24×13
=
1042-312
=
730
=
4.86×[1÷0.01]
=
4.86×100
=
486
四、(1)基础练习,巩固新知
判断下面的简便运算过程是否正确,依据是什么?
1、1024-298=1024-300-2 ( )
2、3.14×6+3.14×4=3.14×(6+4) ( )
3、32×(5×7)=32×7×32×5 ( )
4、723-68+32=723-(68+32) ( )
5、24÷(3+8)=24÷3+24÷8 ( )
√
×
×
×
×
四、(2)综合练习,应用新知
这个长方形的周长是多少厘米?
四、(2)综合练习,应用新知
(46+34)×2
46 ×2 +34×2
哪种方法更简便为什么?
2)一个圆环,外圆的半径是3厘米,内圆的半径
是2厘米,这个圆环的面积是多少平方厘米?
四、(2)综合练习,应用新知
S圆环=πR -πr =π(R - r )
老师这里有三个数字40、8、125,请根据学过的
运算定律,自己编几道式题,并说一说如何运用
运算定律使计算简便?
四、(3)拓展练习,发展新知
能简便的要简便: 评价标准1能够明确运算律的特征,选择合适的运算律。
2 能够明确运算律的特征,选择合适的运算律,书写工整,语言表达条理清晰。
1、287+299
2、125×32×25
3、(1.25+1.25+1.25+1.25)×25×8
4、8.8×125
5、3.46×6.8+65.4×0.68
四、(3)拓展练习,发展新知
1、287+299
=287+300-1
=587-1
=586
2、125×32×25
=125×(8×4)×25
=(125×8)×(4×25)
=1000×100
=100000
四、(3)拓展练习,发展新知
3、(1.25+1.25+1.25+1.25)×25×8
=1.25×4×25×8
=(1.25×8)×(25×4)
=10×100
=1000
四、(3)拓展练习,发展新知
4、8.8×125
=(8+0.8)×125
=8×125+0.8×125
=1000+100
=1100
4、8.8×125
=8×1.1×125
=8×125×1.1
=1000×1.1
=1100
你觉得两种做法,哪一种更好?
评价标准1能够明确运算律的特征,选择合适的运算律。
2 能够明确运算律的特征,选择合适的运算律,书写工整,语言表达条理清晰。
四、(3)拓展练习,发展新知
5、3.46×6.8+65.4×0.68
=3.46×6.8+6.54×6.8
=(3.46+6.54)×6.8
=10×6.8
=68
四、(3)拓展练习,发展新知
四、(3)拓展练习,发展新知
五:梳理总结,提升认知
通过复习你又有哪些收获呢?
评价标准1 能够表述本节课的内容.3分
2能够表述本节课的内容,强调重难点和易错点。5分
36×25
63×73—63×63
421-175-25
125×25×64
72×26+26×48
(每题10分,一共90分)
下面各题,怎样算简便就怎样算
当堂检测。
2.解决问题。
(1)学校买来 72 盒彩色粉笔盒 128 盒白色粉笔,每盒粉笔 40 支,这些粉笔一共多少支
(2)甲、乙两个工程队合修一段路,甲队每天修 70 米,乙队每天修 85 米,11 天正好修完。甲队比乙队一共少修多少米路?
(3)一根长 175 米的绳子,第一次用去了 38 米,第二次用去了 62 米,还剩多少米
(4)张华在新华书店买了 2 本《故事大王》和 2 盒磁带,共花了 36 元,每盒磁带 8 元,每本《故事大王》多少元?
运算律与简便运算总复习
练习巩固
探本溯源,深入理解
知识梳理,形成网络
计算对比,回顾方法
梳理总结,提升认知
当堂检测
学习任务一:计算对比,回顾方法
①:18.93-7.2-2.8=
③1.67×37+0.33×37
②: 7.36-2.36×3=
④:
1
5
÷
6
25
-
2
7
×
7
32
赛一赛:从这四道题中选择两道题做一做,看谁算得又对又快。
你选择了哪两道?为什么?
评价标准
1.算式正确。1分2.结果正确。1分
3.方法适当。1分
4.有条理、清晰的表 达自己的解题思路。1分
应用运算律可以使计算简便。
这些运算律在整数、小数、分数范围内都适用。
我们学过哪些运算律和性质?
二、知识梳理,形成网络
自主整理提纲:
(1)小学阶段学过哪些简便运算律和一些运算性质?
(2)你能按类别有序地、完整地把这些运算定律和运算性质整理好
整理好的同学思考:
在这些运算定律和性质中,最容易“骗”你的是哪种?该注意什么?
评价标准:1知识点梳理系统完整,书写工整,找出并说明易错点。3分
2知识点梳理系统完整,书写工整,图文结合,找出易错点语言表达条理清晰。5分
我们学过哪些运算律和性质?
加法运算律
乘法运算律
运
算
律
交换律:a+b=b+a
交换律:a×b=b×a
结合律:(a+b)+c=a+(b+c)
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
二、知识梳理,形成网络
运
算
性
质
减法性质: a-b-c=a-(b+c)
除法性质: a÷b÷c=a÷ (b×c)
易错简便运算练习要求:
1:先计算各题,怎样算简便就怎样算。写出主要运算步骤。步骤正确1分
2:想一想,对每道题的运算,你改变了什么?你的依据是什么?把你的想法写出来。条理清晰,方法正确1分
3:最后思考,在简便运算中,怎样变是好的变?2分
(1)
(2)
(3)
(4)
(5)
三、探本溯源,深入理解
改变了( )
运算顺序
(1)
= 6
三、探本溯源,深入理解
改变了( )
运算顺序、数值类型
(2)
=
= 6.25
三、探本溯源,深入理解
改变了( )
运算顺序、运算方法
(3) 13.4÷4÷2.5
= 13.4÷(4 × 2.5)
= 1.34
三、探本溯源,深入理解
改变了( )
数值的大小
(4)28÷3.5
28÷3.5
= 56÷7
= 28÷7×2
= 8
= 8
三、探本溯源,深入理解
改变了( )
数值的大小
(5) 435+199
= 435+200-1
= 634
三、探本溯源,深入理解
归纳:
评价标准:1.特点描述准确。1分2.条理清楚的说出什么改变,什么不变。计算方法。2分
1、简便运算中一般有哪几种“变”?
2、为什么要去“变”?
3、“不变”的是什么?
三、探本溯源,深入理解
依据是什么?
依据是( )
乘法结合律、乘法交换律
(1)
三、探本溯源,深入理解
依据是什么?
依据是( )
乘法分配律
(2)
=
三、探本溯源,深入理解
依据是什么?
依据是( )
除法的性质
(3) 13.4÷4÷2.5
= 13.4÷(4 × 2.5)
三、探本溯源,深入理解
依据是什么?
依据是( )
商不变的性质
(4)28÷3.5
= 56÷7
28÷3.5
= 28÷7×2
依据是( )
商的变化规律
三、探本溯源,深入理解
依据是什么?
依据是( )
和的变化规律
(5) 435+199
= 435+200-1
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
166+98=166+100 ( )
一个加数不变,另一个加数增加几,和就会( )。
要使计算结果不变,和必须要( )
2
增加几
减少几
和的变化规律
-
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
146-98=146-100 ( )
被减数不变,减数增加几,差就会( )。
要使计算结果不变,差必须要( )
2
减少几
增加几
差的变化规律
+
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
34×0.5=34×1 ( )
一个因数不变,另一个因数扩大几倍,积就会( )。
要使计算结果不变,积必须要( )
2
扩大相同的倍数
缩小相同的倍数
积的变化规律
÷
三、探本溯源,深入理解
根据例子归纳和、差、积、商的变化规律:
34÷0.5=34÷1 ( )
被除数不变,除数扩大几倍,商就会( )。
要使计算结果不变,商必须要( )
2
缩小相同的倍数
扩大相同的倍数
商的变化规律
×
三、探本溯源,深入理解
(1). 25×48=25×(40+8)
=25×40+25×8=1000+200=120
应用了( )。
(2)25×48=25×(6×8)=6×(25×8)
=6×200=1200
应用了( )。
(3)25×48=25×(50-2)
=25×50-25×2=1250-50=1200
应用了( )。
1、25×48的几种计算方法,分别应用了哪个运算定律?
乘法分配律
乘法结合律
乘法分配律
四、(1)基础练习,巩固新知
2.计算下列各题,能简算的要简算。评价标准:计算正确简便方法合理.5分一题
四、(1)基础练习,巩固新知
2000-197
8.8-6.75+9.2-0.25
41×102
0.8×3.6-0.8×0.6
=
2000-200+3
=
1800+3
=
1803
=
(8.8+9.2)
-
(6.75+0.25)
=
18
-
7
=
11
=
41×(100+2)
=
41×100+41×2
=
4100+82
=
4182
=
0.8×(3.6-0.6)
=
0.8×3
=
2.4
2.计算下列各题,能简算的要简算。
=
=
=
=
=
=
1
5
÷
6
25
-
2
7
×
7
32
7
12
+
3
8
-
23
24
×
(
)
24
1
5
×
25
6
-
2
7
×
7
32
1
5
1
1
16
1
1
16
5
6
-
14+9-23
0
3
48
40
48
-
=
37
48
-
23
24
×
24
7
12
24
×
+
3
8
24
×
四、(1)基础练习,巩固新知
2.计算下列各题,能简算的要简算。
1042-384÷16×13
4.86×[1÷(2.1-2.09)]
=
1042-24×13
=
1042-312
=
730
=
4.86×[1÷0.01]
=
4.86×100
=
486
四、(1)基础练习,巩固新知
判断下面的简便运算过程是否正确,依据是什么?
1、1024-298=1024-300-2 ( )
2、3.14×6+3.14×4=3.14×(6+4) ( )
3、32×(5×7)=32×7×32×5 ( )
4、723-68+32=723-(68+32) ( )
5、24÷(3+8)=24÷3+24÷8 ( )
√
×
×
×
×
四、(2)综合练习,应用新知
这个长方形的周长是多少厘米?
四、(2)综合练习,应用新知
(46+34)×2
46 ×2 +34×2
哪种方法更简便为什么?
2)一个圆环,外圆的半径是3厘米,内圆的半径
是2厘米,这个圆环的面积是多少平方厘米?
四、(2)综合练习,应用新知
S圆环=πR -πr =π(R - r )
老师这里有三个数字40、8、125,请根据学过的
运算定律,自己编几道式题,并说一说如何运用
运算定律使计算简便?
四、(3)拓展练习,发展新知
能简便的要简便: 评价标准1能够明确运算律的特征,选择合适的运算律。
2 能够明确运算律的特征,选择合适的运算律,书写工整,语言表达条理清晰。
1、287+299
2、125×32×25
3、(1.25+1.25+1.25+1.25)×25×8
4、8.8×125
5、3.46×6.8+65.4×0.68
四、(3)拓展练习,发展新知
1、287+299
=287+300-1
=587-1
=586
2、125×32×25
=125×(8×4)×25
=(125×8)×(4×25)
=1000×100
=100000
四、(3)拓展练习,发展新知
3、(1.25+1.25+1.25+1.25)×25×8
=1.25×4×25×8
=(1.25×8)×(25×4)
=10×100
=1000
四、(3)拓展练习,发展新知
4、8.8×125
=(8+0.8)×125
=8×125+0.8×125
=1000+100
=1100
4、8.8×125
=8×1.1×125
=8×125×1.1
=1000×1.1
=1100
你觉得两种做法,哪一种更好?
评价标准1能够明确运算律的特征,选择合适的运算律。
2 能够明确运算律的特征,选择合适的运算律,书写工整,语言表达条理清晰。
四、(3)拓展练习,发展新知
5、3.46×6.8+65.4×0.68
=3.46×6.8+6.54×6.8
=(3.46+6.54)×6.8
=10×6.8
=68
四、(3)拓展练习,发展新知
四、(3)拓展练习,发展新知
五:梳理总结,提升认知
通过复习你又有哪些收获呢?
评价标准1 能够表述本节课的内容.3分
2能够表述本节课的内容,强调重难点和易错点。5分
36×25
63×73—63×63
421-175-25
125×25×64
72×26+26×48
(每题10分,一共90分)
下面各题,怎样算简便就怎样算
当堂检测。
2.解决问题。
(1)学校买来 72 盒彩色粉笔盒 128 盒白色粉笔,每盒粉笔 40 支,这些粉笔一共多少支
(2)甲、乙两个工程队合修一段路,甲队每天修 70 米,乙队每天修 85 米,11 天正好修完。甲队比乙队一共少修多少米路?
(3)一根长 175 米的绳子,第一次用去了 38 米,第二次用去了 62 米,还剩多少米
(4)张华在新华书店买了 2 本《故事大王》和 2 盒磁带,共花了 36 元,每盒磁带 8 元,每本《故事大王》多少元?
同课章节目录
