人教版七年级数学下册9.1.1 不等式1课时 课件(共20张PPT)
文档属性
| 名称 | 人教版七年级数学下册9.1.1 不等式1课时 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
9.1 不等式
9.1.1 不等式及其解集
人教版 数学 七年级 下册
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
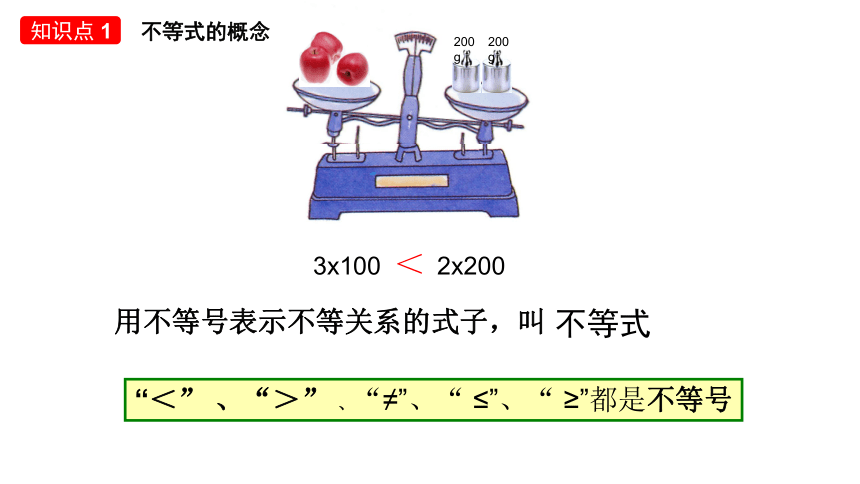
200g
200g
3x100 2x200
<
不等式
用不等号表示不等关系的式子,叫
“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
知识点 1
不等式的概念
例1 判断下列式子是不是不等式:
① -1<3; ② -x+2=4;
③ 3x ≠ 4y; ④ 6 > 2;
⑤ 2x -3; ⑥ 2m < n.
是;
不是;
是;
是;
不是;
是.
探究新知
素养考点 1
不等式的识别
(1) a与1的和是正数;
(2)y的2倍与1的和小于3;
(3) y的3倍与x的2倍的和是非负数
(4) x乘以3的积加上2最多为5.
(1) a+1>0;
(2)2y+1<3;
(3)3y+2x≥0;
(4)3x+2≤5.
例2 用不等式表示:
解:
素养考点 2
用不等式表示数量关系
探究新知
a是正数: a是负数:
a是非正数: a是非负数:
a不大于b: a 不小于b:
a超过b: a不超过b:
a不等于b:
小结:常用不等关系
a>0
a<0
a≤0
a≥0
a≤b
a≥b
a≠b
a≤b
a>b
观察下列不等式:
(1)2x-2.5≥15; (2)x≤8.75;
(3)x<4; (4)5+3y>240.
这些不等式有哪些共同特点 (未知数个数,次数)
共同特点: 这些不等式的两边都是整式,只含一个未知数、并且含未知数的项次数为1 .
一元一次不等式
类比思想
练一练
指出下列中哪些是一元一次不等式
1 . 3z-3≤5
2 . 6a-b<9
3 . 7.5X≤8
≥
4.
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,同样,
能使不等式成立的未知数的值叫不等式的解.
判断下列数中哪些是不等式 2x >50的解:
70 , 60 , 25 , 20, 10, 0 ,-5
你还能找出这个不等式的其他解吗 请举出例子。
这个不等式有多少个解
无数个解
知识点 2
不等式的解和解集
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
【讨论】不等式的解和不等式的解集是一样的吗
求不等式的解集的过程叫解不等式.
探究新知
如:2x >50 的解集是
练习:下列说法正确的是( )
A. x=3不是2x>1的解
B. 2x>1的解是x=3
C. x=3是2x>1的解
D. x=3是2x>1的解集
C
4.不等式解集的表示方法
第一种:用式子x>a, x例3. 用数轴表示下列不等式的解集:
⑴ x>-1; ⑵ x< 9 (3)x ≥-1
○
0
-1
⑴
解:
总结: 用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
第二种:利用数轴表示不等式的解集.
0
⑵
。
9
“>” “<”是空心; “≥” “≤”是实心
“>” “≥”向右画; “<” “≤” 向左画
0
-1
(3)
●
在数轴上表示下列不等式的解集:
(1) x>-1; (2) x≥-1;
(3) x<-1; (4) x≤-1.
分析:画数轴,定界点,走方向的步骤作答.
答案:如图:
巩固练习
0
1
2
例 直接写出x+4<6的解集,并在数轴上表示出来.
解:x<2.
这个解集可以在数轴上表示为:
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
变式1:已知x的解集如图所示,你能写出x的解集吗
素养考点 1
探究新知
在数轴上表示不等式解集
变式2:直接写出不等式2x>8的解集,并在数轴上表示出来.
解:x>4.
这个解集在数轴上表示为:
0
4
变式3:直接写出不等式-2x>8的解集.
解:x<-4.
探究新知
○
0
-3
⑴
○
0
-5
⑶
●
0
2
⑵
●
0
a
⑷
写出下列数轴所表示的不等式的解集:
x > -3
x ≥ 2
x< -5
x ≤ a
练习:
巩固练习
不等式
→
实际问题中不等式的表示
概念
↓
↓
解、解集
课堂小结
1、用不等式表示:
(1)a与5的和是正数
(2)a与15的和小于27
(3)a与2的差是非负数
(4)d与e的差不大于-2
课堂检测
3、在数轴上表示不等式 3x≥6 的解集,正确的是( )
0
1
2
0
1
2
0
1
2
0
1
2
(A)
(B)
(C)
(D)
D
2、下列数值哪些是不等式x+4>6的解?哪些不是?
-4, -2.5 ,0, 1, 2.5, 3, 3.2, 4.8, 8, 12
√
√
√
√
√ √
课堂检测
4、请你试着直接写出下列不等式的解集.
(1)2x<8
(2)x-2>0
(3) 2x+1<3
(4) a2+1>0
不等式2x<8的解集是: x<4
不等式x-2>0的解集是: x>2
不等式2x+1<3的解集是: x<1
不等式a2+1>0的解集是: a取任何数
5、当x>1时,不等式x+5>3成立,则“x>1是不等式x+5>3 的解集”是否正确,为什么?
课堂检测
1、适合不等式x-3<0的非负整数是哪几个数?
适合不等式x+3>0的非正整数有哪几个?分别求出来.
2、求出适合不等式-2≤a≤5的整数(不等式的整数解),
同时适合不等式 -2< a<5 的整数是哪几个?
拓广探索题
课堂检测
9.1 不等式
9.1.1 不等式及其解集
人教版 数学 七年级 下册
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
200g
200g
3x100 2x200
<
不等式
用不等号表示不等关系的式子,叫
“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
知识点 1
不等式的概念
例1 判断下列式子是不是不等式:
① -1<3; ② -x+2=4;
③ 3x ≠ 4y; ④ 6 > 2;
⑤ 2x -3; ⑥ 2m < n.
是;
不是;
是;
是;
不是;
是.
探究新知
素养考点 1
不等式的识别
(1) a与1的和是正数;
(2)y的2倍与1的和小于3;
(3) y的3倍与x的2倍的和是非负数
(4) x乘以3的积加上2最多为5.
(1) a+1>0;
(2)2y+1<3;
(3)3y+2x≥0;
(4)3x+2≤5.
例2 用不等式表示:
解:
素养考点 2
用不等式表示数量关系
探究新知
a是正数: a是负数:
a是非正数: a是非负数:
a不大于b: a 不小于b:
a超过b: a不超过b:
a不等于b:
小结:常用不等关系
a>0
a<0
a≤0
a≥0
a≤b
a≥b
a≠b
a≤b
a>b
观察下列不等式:
(1)2x-2.5≥15; (2)x≤8.75;
(3)x<4; (4)5+3y>240.
这些不等式有哪些共同特点 (未知数个数,次数)
共同特点: 这些不等式的两边都是整式,只含一个未知数、并且含未知数的项次数为1 .
一元一次不等式
类比思想
练一练
指出下列中哪些是一元一次不等式
1 . 3z-3≤5
2 . 6a-b<9
3 . 7.5X≤8
≥
4.
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,同样,
能使不等式成立的未知数的值叫不等式的解.
判断下列数中哪些是不等式 2x >50的解:
70 , 60 , 25 , 20, 10, 0 ,-5
你还能找出这个不等式的其他解吗 请举出例子。
这个不等式有多少个解
无数个解
知识点 2
不等式的解和解集
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
【讨论】不等式的解和不等式的解集是一样的吗
求不等式的解集的过程叫解不等式.
探究新知
如:2x >50 的解集是
练习:下列说法正确的是( )
A. x=3不是2x>1的解
B. 2x>1的解是x=3
C. x=3是2x>1的解
D. x=3是2x>1的解集
C
4.不等式解集的表示方法
第一种:用式子x>a, x例3. 用数轴表示下列不等式的解集:
⑴ x>-1; ⑵ x< 9 (3)x ≥-1
○
0
-1
⑴
解:
总结: 用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
第二种:利用数轴表示不等式的解集.
0
⑵
。
9
“>” “<”是空心; “≥” “≤”是实心
“>” “≥”向右画; “<” “≤” 向左画
0
-1
(3)
●
在数轴上表示下列不等式的解集:
(1) x>-1; (2) x≥-1;
(3) x<-1; (4) x≤-1.
分析:画数轴,定界点,走方向的步骤作答.
答案:如图:
巩固练习
0
1
2
例 直接写出x+4<6的解集,并在数轴上表示出来.
解:x<2.
这个解集可以在数轴上表示为:
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
变式1:已知x的解集如图所示,你能写出x的解集吗
素养考点 1
探究新知
在数轴上表示不等式解集
变式2:直接写出不等式2x>8的解集,并在数轴上表示出来.
解:x>4.
这个解集在数轴上表示为:
0
4
变式3:直接写出不等式-2x>8的解集.
解:x<-4.
探究新知
○
0
-3
⑴
○
0
-5
⑶
●
0
2
⑵
●
0
a
⑷
写出下列数轴所表示的不等式的解集:
x > -3
x ≥ 2
x< -5
x ≤ a
练习:
巩固练习
不等式
→
实际问题中不等式的表示
概念
↓
↓
解、解集
课堂小结
1、用不等式表示:
(1)a与5的和是正数
(2)a与15的和小于27
(3)a与2的差是非负数
(4)d与e的差不大于-2
课堂检测
3、在数轴上表示不等式 3x≥6 的解集,正确的是( )
0
1
2
0
1
2
0
1
2
0
1
2
(A)
(B)
(C)
(D)
D
2、下列数值哪些是不等式x+4>6的解?哪些不是?
-4, -2.5 ,0, 1, 2.5, 3, 3.2, 4.8, 8, 12
√
√
√
√
√ √
课堂检测
4、请你试着直接写出下列不等式的解集.
(1)2x<8
(2)x-2>0
(3) 2x+1<3
(4) a2+1>0
不等式2x<8的解集是: x<4
不等式x-2>0的解集是: x>2
不等式2x+1<3的解集是: x<1
不等式a2+1>0的解集是: a取任何数
5、当x>1时,不等式x+5>3成立,则“x>1是不等式x+5>3 的解集”是否正确,为什么?
课堂检测
1、适合不等式x-3<0的非负整数是哪几个数?
适合不等式x+3>0的非正整数有哪几个?分别求出来.
2、求出适合不等式-2≤a≤5的整数(不等式的整数解),
同时适合不等式 -2< a<5 的整数是哪几个?
拓广探索题
课堂检测
