华东师大版八年级数学下册 19.1.2矩形的判定 课件(共18张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册 19.1.2矩形的判定 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1005.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 07:39:39 | ||
图片预览



文档简介
(共18张PPT)
19.1.2 矩形的判定
回顾旧知
1、矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
2、矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
新知探究
思考探究:如何判定一个四边形是矩形?
定义法:有一个角是直角的平行四边形是矩形.
(1、平行四边形 2、有一个角是直角)
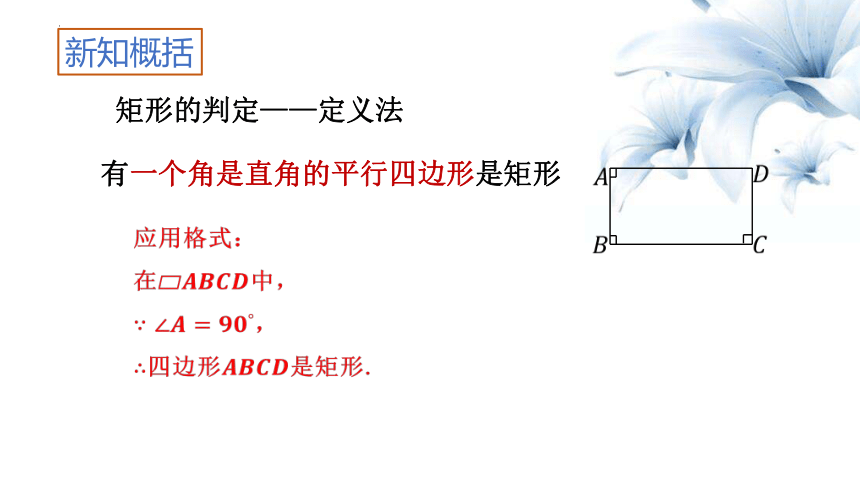
矩形的判定——定义法
有一个角是直角的平行四边形是矩形
应用格式:
在中,
,
四边形是矩形.
新知概括
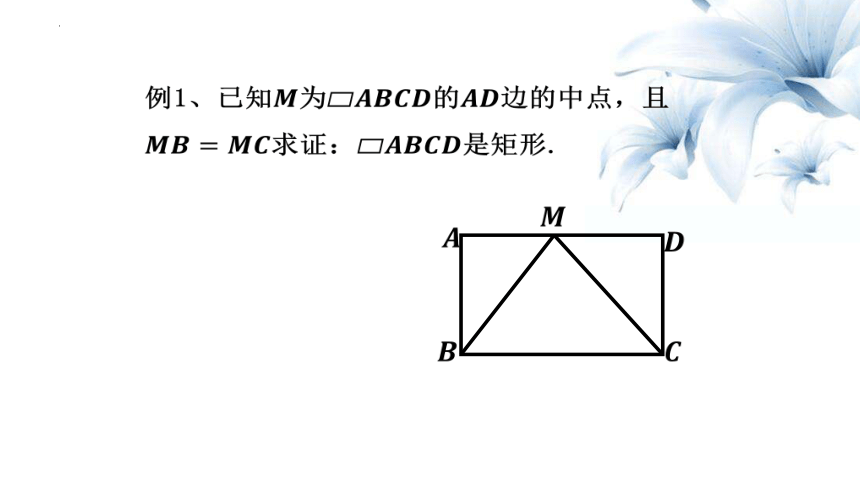
例1、已知为的边的中点,且求证:是矩形.
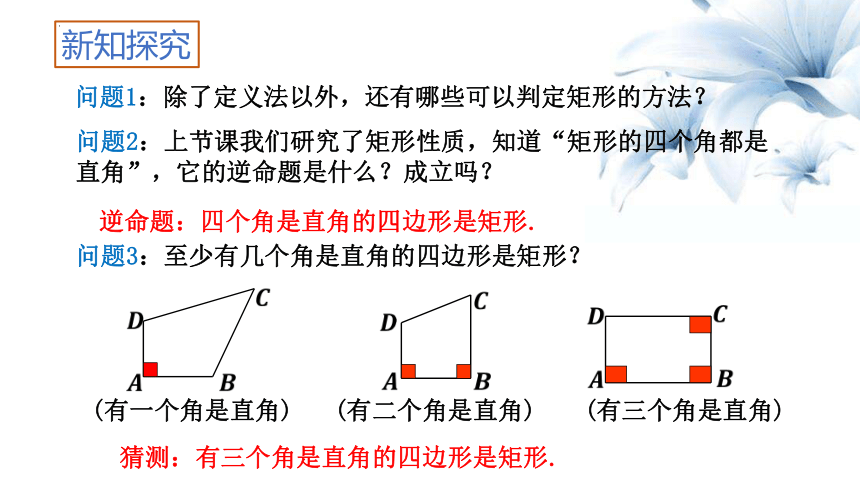
问题1:除了定义法以外,还有哪些可以判定矩形的方法?
新知探究
问题2:上节课我们研究了矩形性质,知道“矩形的四个角都是直角”,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
问题3:至少有几个角是直角的四边形是矩形?
(有一个角是直角)
(有二个角是直角)
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
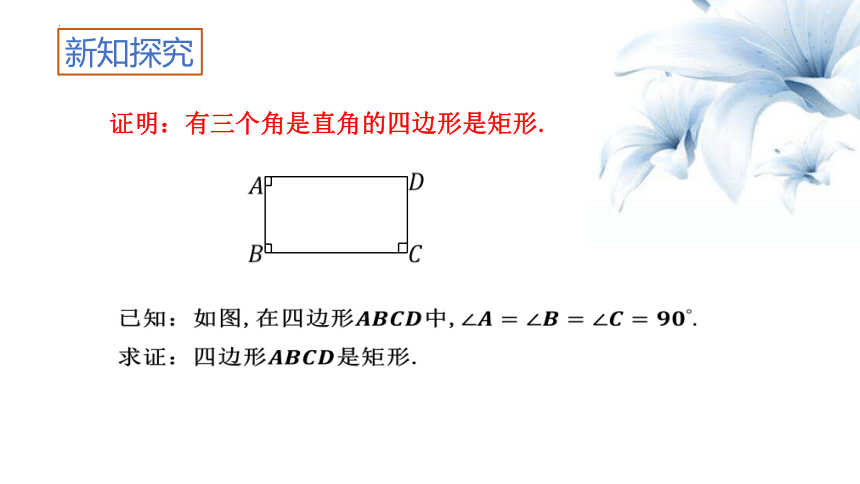
证明:有三个角是直角的四边形是矩形.
已知:如图,在四边形中,
求证:四边形是矩形.
新知探究
矩形的判定定理1:
有三个角是直角的四边形是矩形
应用格式:
在四边形中,
,
四边形是矩形.
新知概括
例2、如图,四边形是由两个全等的正三角形和组成的,、分别为、 的中点.
求证:四边形是矩形.
问题1:上节课我们已经知道“矩形的对角线相等”,反过来,“对角线相等的四边形是矩形”,你觉得对吗?
新知探究
问题2:怎么添加一个限制条件,才能用“对角线相等”判定矩形呢?
猜测:对角线相等的平行四边形是矩形.
证明:对角线相等的平行四边形是矩形.
已知:如图,四边形是平行四边形,.
求证:四边形是矩形.
新知探究
矩形的判定定理2:
对角线相等的平行四边形是矩形
应用格式:
在中,
,
四边形是矩形.
新知概括
判定矩形的常规思路:
新知概括
例3、如图,点是矩形的对角线与的交点,、、、分别是、、、上的一点,且.求证:四边形是矩形.
练习、下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(6)有一个角是直角的四边形是矩形;
(8)有三个角是直角的四边形是矩形;
(9)四个角都相等的四边形是矩形;
(3)对角线相等且有一个内角是直角的四边形是矩形;
(5)对角线相等且互相垂直的四边形是矩形;
(10)一组对角互补的平行四边形是矩形.
(7)有三个角都相等的四边形是矩形;
(4)对角线互相垂直平分的四边形是矩形.
课堂小结
例4、如图,在中,,,垂足为点,是的外角的平分线,∥,交于点.
求证:四边形是矩形.
例5、如图,在中,以为斜边作,且,试说明四边形是矩形.
19.1.2 矩形的判定
回顾旧知
1、矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
2、矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
新知探究
思考探究:如何判定一个四边形是矩形?
定义法:有一个角是直角的平行四边形是矩形.
(1、平行四边形 2、有一个角是直角)
矩形的判定——定义法
有一个角是直角的平行四边形是矩形
应用格式:
在中,
,
四边形是矩形.
新知概括
例1、已知为的边的中点,且求证:是矩形.
问题1:除了定义法以外,还有哪些可以判定矩形的方法?
新知探究
问题2:上节课我们研究了矩形性质,知道“矩形的四个角都是直角”,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
问题3:至少有几个角是直角的四边形是矩形?
(有一个角是直角)
(有二个角是直角)
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
证明:有三个角是直角的四边形是矩形.
已知:如图,在四边形中,
求证:四边形是矩形.
新知探究
矩形的判定定理1:
有三个角是直角的四边形是矩形
应用格式:
在四边形中,
,
四边形是矩形.
新知概括
例2、如图,四边形是由两个全等的正三角形和组成的,、分别为、 的中点.
求证:四边形是矩形.
问题1:上节课我们已经知道“矩形的对角线相等”,反过来,“对角线相等的四边形是矩形”,你觉得对吗?
新知探究
问题2:怎么添加一个限制条件,才能用“对角线相等”判定矩形呢?
猜测:对角线相等的平行四边形是矩形.
证明:对角线相等的平行四边形是矩形.
已知:如图,四边形是平行四边形,.
求证:四边形是矩形.
新知探究
矩形的判定定理2:
对角线相等的平行四边形是矩形
应用格式:
在中,
,
四边形是矩形.
新知概括
判定矩形的常规思路:
新知概括
例3、如图,点是矩形的对角线与的交点,、、、分别是、、、上的一点,且.求证:四边形是矩形.
练习、下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(6)有一个角是直角的四边形是矩形;
(8)有三个角是直角的四边形是矩形;
(9)四个角都相等的四边形是矩形;
(3)对角线相等且有一个内角是直角的四边形是矩形;
(5)对角线相等且互相垂直的四边形是矩形;
(10)一组对角互补的平行四边形是矩形.
(7)有三个角都相等的四边形是矩形;
(4)对角线互相垂直平分的四边形是矩形.
课堂小结
例4、如图,在中,,,垂足为点,是的外角的平分线,∥,交于点.
求证:四边形是矩形.
例5、如图,在中,以为斜边作,且,试说明四边形是矩形.
