2020-2021学年苏科版八年级数学下册 反比例函数中的矩形问题 课件(共17张PPT)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学下册 反比例函数中的矩形问题 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
反比例函数中的矩形问题
教学目标:
1、探索反比例函数图象截矩形两边线段成比例;
2、发展模型思想,运用基本模型解决问题;
3、通过探索的过程,锻炼学生逻辑能力、发散思维能力。
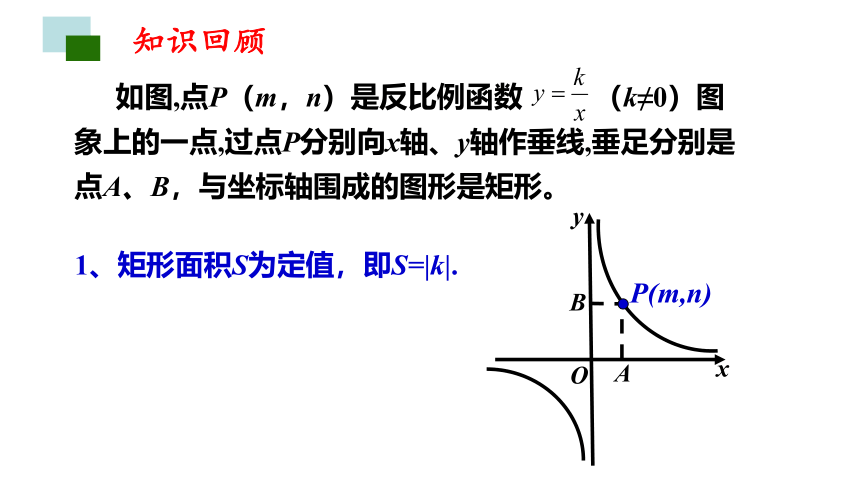
P(m,n)
如图,点P(m,n)是反比例函数 (k≠0)图象上的一点,过点P分别向x轴、y轴作垂线,垂足分别是点A、B,与坐标轴围成的图形是矩形。
x
y
O
A
B
1、矩形面积S为定值,即S=|k|.
知识回顾
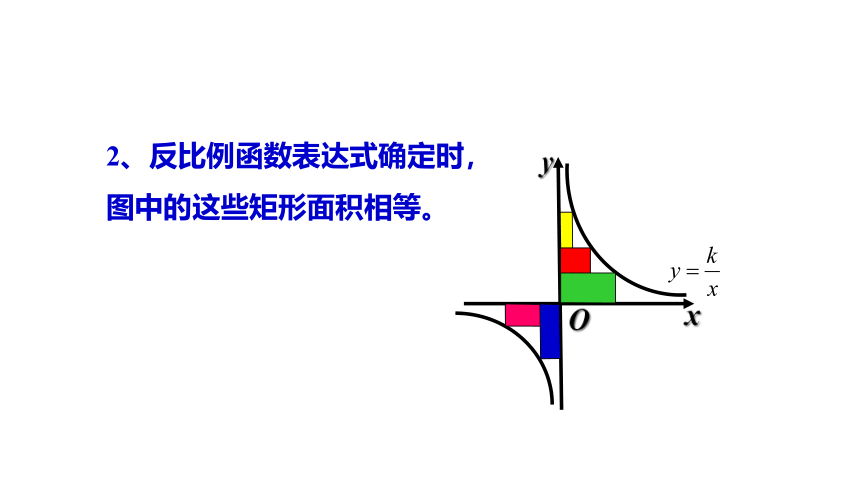
x
y
O
2、反比例函数表达式确定时,
图中的这些矩形面积相等。
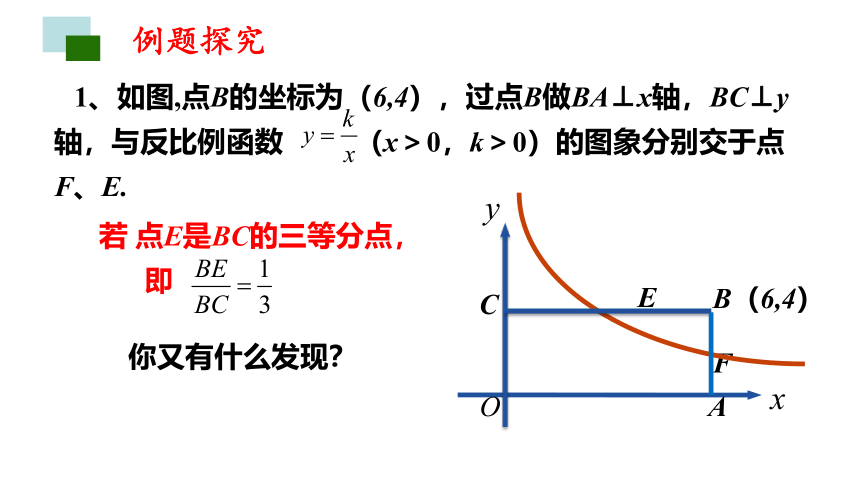
例题探究
1、如图,点B的坐标为(6,4),过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(6,4)
A
你有什么发现?
若 点E是BC的中点
·
例题探究
1、如图,点B的坐标为(6,4),过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(6,4)
A
你又有什么发现?
若 点E是BC的三等分点,
即
例题探究
1、如图,点B的坐标为(6,4),过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(6,4)
A
你有什么样的猜想?
若 点E是BC上的任意点,
例题探究
1、如图, ,过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(a,b)
A
刚才的结论仍然成立吗?
若 点E是BC上的任意点,
点B的坐标为(a,b)
例题拓展
1、如图, ,过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(a,b)
A
若 点E是BC上的任意点,
点B的坐标为(a,b)
连接EF,AC;
判断EF与AC的位置关系,并证明;
规律总结
1、如图, ,过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(a,b)
A
若 点E是BC上的任意点,
点B的坐标为(a,b)
1.
2. EF∥AC
1.(2021 复习指导)矩形AOBC中,OB=4,OA=3。分别以OA,OB所在直线为x轴,y轴建立如图所示的平面直角坐标系。F是边BC上一个动点(不与B,C重合),过点F的反比例函数 (k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,
点E的坐标( , );
(2)连接EF,tan∠EFC = ;
课堂精练
2、(2015·徐州改编)在矩形OABC中,OA=3,OC=5.分别以OA,OC所在直线为x轴、y轴,建立平面直角坐标系.D是边CB上的一个动点(不与C、B重合),反比例函数 (k>0)的图象经过点D且与边BA交于点E,连接DE.
判断:连接CA,DE与CA是否平行?请说明理由;
课堂精练
深入探究
如图,点P的坐标为(1,-2),过点P做PC⊥x轴,PD⊥y轴,反比例函数表达式为 (k>0);
y
x
O
C
P(1,-2)
D
B
A
·
延长PC, PD与反比例图像交于点B, A;
仍然有 吗?
(2014·徐州改编)如图,将透明三角形片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数 图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴、y轴相交于点E、F、已知B(1,3).
(1)k=________;
(2)试说明CD∥AB
(3)试说明AE=BF
课后思考
(1)延长EF,与x轴,y轴,分别交于点H,G
GE与FH 相等吗?
y
O
E
F
C
B(a,b)
A
y
O
E
F
G
H
·
·
(2)若点E,F是反比例函数图像上任意两个不同的点,
GE与FH 还相等吗?
课后思考
y
x
O
C
P
D
E
F
·
(3)若点E,F在不同支上;
GE=FH仍然成立吗?
·
·
H
G
C`
D`
P`
·
谢谢!
反比例函数中的矩形问题
教学目标:
1、探索反比例函数图象截矩形两边线段成比例;
2、发展模型思想,运用基本模型解决问题;
3、通过探索的过程,锻炼学生逻辑能力、发散思维能力。
P(m,n)
如图,点P(m,n)是反比例函数 (k≠0)图象上的一点,过点P分别向x轴、y轴作垂线,垂足分别是点A、B,与坐标轴围成的图形是矩形。
x
y
O
A
B
1、矩形面积S为定值,即S=|k|.
知识回顾
x
y
O
2、反比例函数表达式确定时,
图中的这些矩形面积相等。
例题探究
1、如图,点B的坐标为(6,4),过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(6,4)
A
你有什么发现?
若 点E是BC的中点
·
例题探究
1、如图,点B的坐标为(6,4),过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(6,4)
A
你又有什么发现?
若 点E是BC的三等分点,
即
例题探究
1、如图,点B的坐标为(6,4),过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(6,4)
A
你有什么样的猜想?
若 点E是BC上的任意点,
例题探究
1、如图, ,过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(a,b)
A
刚才的结论仍然成立吗?
若 点E是BC上的任意点,
点B的坐标为(a,b)
例题拓展
1、如图, ,过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(a,b)
A
若 点E是BC上的任意点,
点B的坐标为(a,b)
连接EF,AC;
判断EF与AC的位置关系,并证明;
规律总结
1、如图, ,过点B做BA⊥x轴,BC⊥y轴,与反比例函数 (x>0,k>0)的图象分别交于点F、E.
y
x
O
E
F
C
B(a,b)
A
若 点E是BC上的任意点,
点B的坐标为(a,b)
1.
2. EF∥AC
1.(2021 复习指导)矩形AOBC中,OB=4,OA=3。分别以OA,OB所在直线为x轴,y轴建立如图所示的平面直角坐标系。F是边BC上一个动点(不与B,C重合),过点F的反比例函数 (k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,
点E的坐标( , );
(2)连接EF,tan∠EFC = ;
课堂精练
2、(2015·徐州改编)在矩形OABC中,OA=3,OC=5.分别以OA,OC所在直线为x轴、y轴,建立平面直角坐标系.D是边CB上的一个动点(不与C、B重合),反比例函数 (k>0)的图象经过点D且与边BA交于点E,连接DE.
判断:连接CA,DE与CA是否平行?请说明理由;
课堂精练
深入探究
如图,点P的坐标为(1,-2),过点P做PC⊥x轴,PD⊥y轴,反比例函数表达式为 (k>0);
y
x
O
C
P(1,-2)
D
B
A
·
延长PC, PD与反比例图像交于点B, A;
仍然有 吗?
(2014·徐州改编)如图,将透明三角形片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数 图象的两支上,且PB⊥x轴于点C,PA⊥y轴于点D,AB分别与x轴、y轴相交于点E、F、已知B(1,3).
(1)k=________;
(2)试说明CD∥AB
(3)试说明AE=BF
课后思考
(1)延长EF,与x轴,y轴,分别交于点H,G
GE与FH 相等吗?
y
O
E
F
C
B(a,b)
A
y
O
E
F
G
H
·
·
(2)若点E,F是反比例函数图像上任意两个不同的点,
GE与FH 还相等吗?
课后思考
y
x
O
C
P
D
E
F
·
(3)若点E,F在不同支上;
GE=FH仍然成立吗?
·
·
H
G
C`
D`
P`
·
谢谢!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
