湖南省邵阳市绥宁县2021-2022学年八年级下学期期中考试数学试题(word版含答案)
文档属性
| 名称 | 湖南省邵阳市绥宁县2021-2022学年八年级下学期期中考试数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 634.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 07:36:10 | ||
图片预览


文档简介
湖南省邵阳市绥宁县2021-2022学年八年级下学期期中考试数学试题
温馨提示;本试卷共三道大题,满分120分,考试时量90分钟。
一、选择题(本大题共10 个小题,每小题3分,共30分)
1、下列图案中,既是轴对称图形又是中心对称图形的是
2、若△ABC的三边长分别为a、b、c,下列条件中能判断△ABC是直角三角形的有
①∠A=∠B-∠C,②∠A:∠B:∠C=3:4:5,③∠A=90°-∠B,④∠A=∠B=∠C⑤a =(b+c)(b-c),⑥a∶b:c=5∶12∶13.
A.3个 B.4个 C.5个 D.6个
3、点M在第二象限,它到x轴的距离为1,到y轴的距离为2,则点M的坐标是
A.(-2,1) B.(2,-1) C.(1,-2) D.(-1,2)
4、以下列各组数为三角形的三条边长∶①1,,3;②9,40,41;③,,2;④1.5,2.5,2.其中能构成直角三角形的有
A.1 组 B.2组 C.3组 D.4组
5、下列条件中,不能判定两个直角三角形全等的是
A.一个锐角和斜边对应相等B.两条直角边对应相等
C.两个锐角对应相等D.斜边和一直角边对应相等
6、下列说法正确的有
①对角线互相平分的四边形是平行四边形②对角线相等的四边形是矩形
③对角线,互相垂直的四边形是菱形④对角线相等的平行四边形是矩形
⑤对角线互相垂直且相等的平行四边形是正方形
A.1个 B.2个 C.3个 D.4个
7、如图,一根木棍(AB),斜靠在与地面(OM)垂直的墙(OM)上,当木棍A端沿墙下滑,且B端沿地面向右滑行时,AB 的中点P到点O的距离
A.变大力下 B. 变小 C.先变小后变大 D.不变
第7题图 第8题图 第9题图 第10题图
8、如图,下列条件之一能使平行四边形 ABCD是菱形的为
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③B.②③C.③④D.①②③
9、在数学活动课上,小明提出这样一个问题∶如图,∠B=∠C=90°,E是 BC的
中点,DE 平分∠ADC,则下列说法正确的有
①AB//CD;②AE平分∠DAB;③△EBA≌△DCE;④AB+CD=AD;⑤ME⊥DE.
A.2个 B.3个 C.4个 D.5个
10、如图,在四边形ABCD中,AB//DC,AD=BC=5,DC=7,AB=13,点P从点A 出发以3个单位/s的速度沿 AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA 向终点A运动.当四边形 PQBC为平行四边形时,运动时间为
A.4s B.3s C.2s D.1s
二、填空题(本大题共8个小题,每小题3分,共24分)
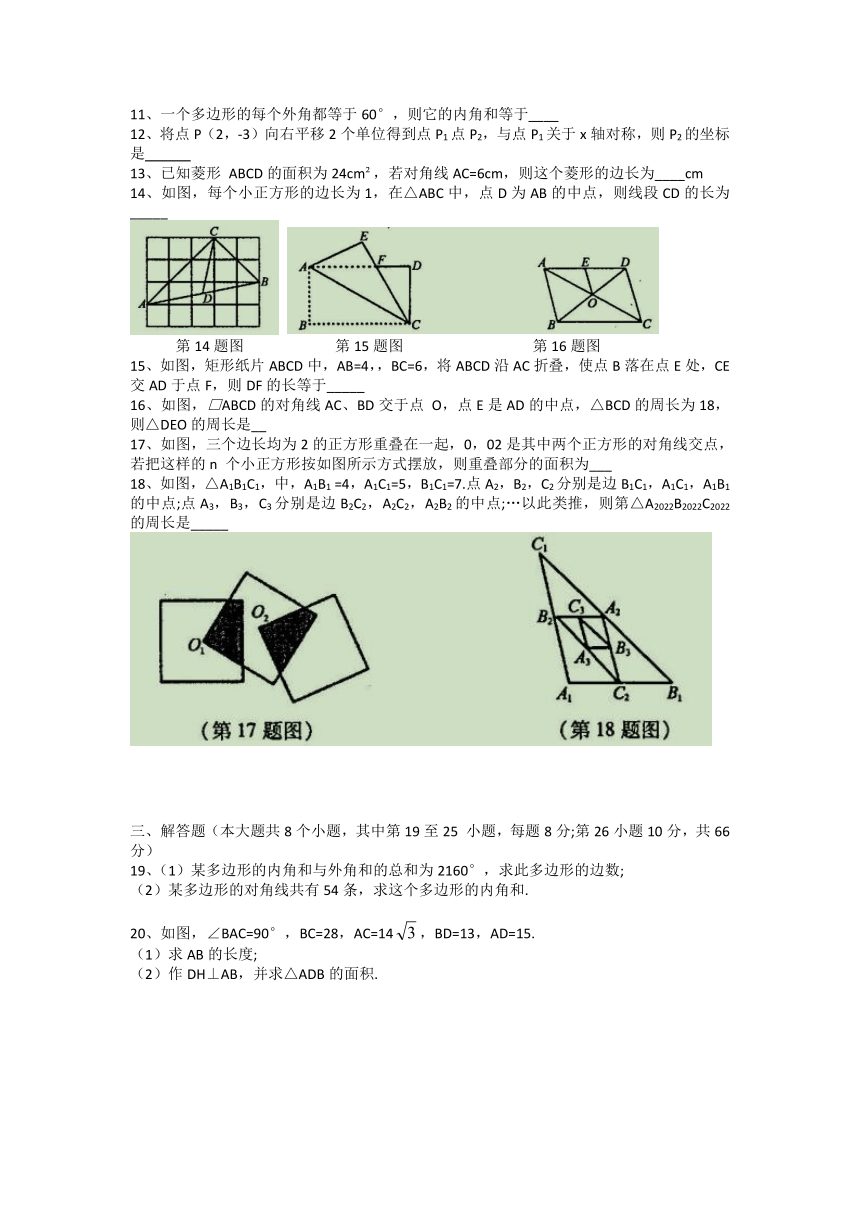
11、一个多边形的每个外角都等于60°,则它的内角和等于____
12、将点P(2,-3)向右平移2个单位得到点P1点P2,与点P1关于x轴对称,则P2的坐标是
13、已知菱形 ABCD的面积为24cm ,若对角线AC=6cm,则这个菱形的边长为____cm
14、如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为_____
第14题图 第15题图 第16题图
15、如图,矩形纸片ABCD中,AB=4,,BC=6,将ABCD沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于_____
16、如图,□ABCD的对角线AC、BD交于点 O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是__
17、如图,三个边长均为2的正方形重叠在一起,0,02是其中两个正方形的对角线交点,若把这样的n 个小正方形按如图所示方式摆放,则重叠部分的面积为___
18、如图,△A1B1C1,中,A1B1 =4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…以此类推,则第△A2022B2022C2022的周长是_____
解答题(本大题共8个小题,其中第19至25 小题,每题8分;第26小题10分,共66分)
19、(1)某多边形的内角和与外角和的总和为2160°,求此多边形的边数;
(2)某多边形的对角线共有54条,求这个多边形的内角和.
20、如图,∠BAC=90°,BC=28,AC=14,BD=13,AD=15.
(1)求AB的长度;
(2)作DH⊥AB,并求△ADB的面积.
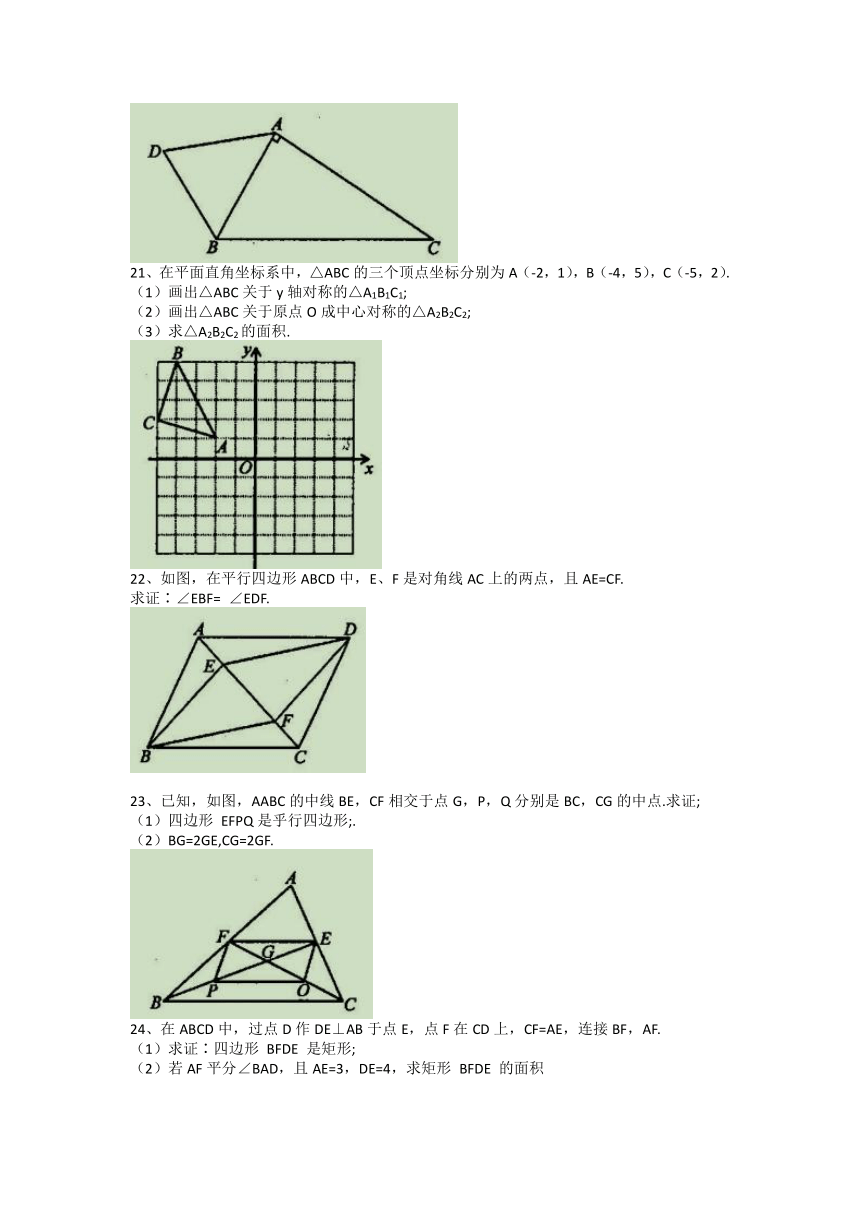
21、在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2;
(3)求△A2B2C2的面积.
22、如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.
求证∶∠EBF= ∠EDF.
23、已知,如图,AABC的中线BE,CF相交于点G,P,Q分别是BC,CG的中点.求证;
(1)四边形 EFPQ是乎行四边形;.
(2)BG=2GE,CG=2GF.
24、在ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证∶四边形 BFDE 是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形 BFDE 的面积
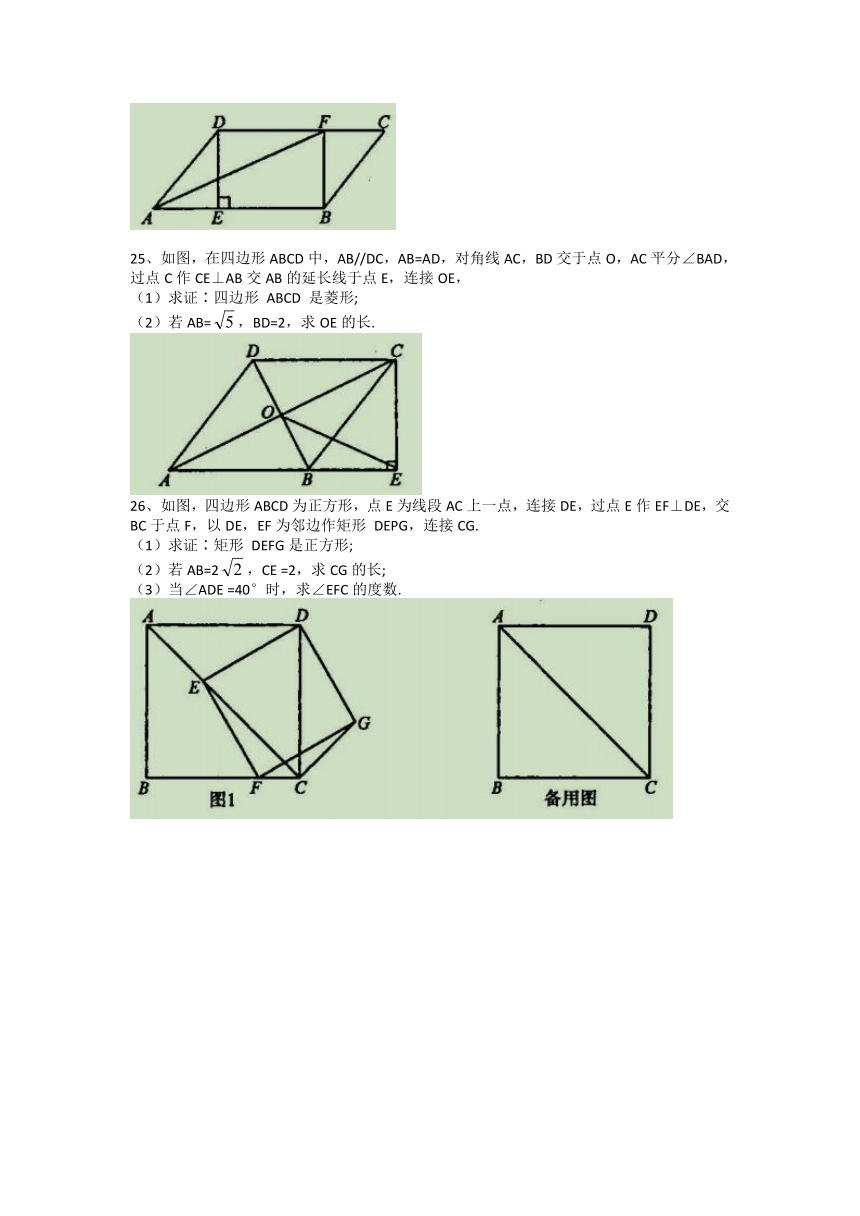
如图,在四边形ABCD中,AB//DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE,
求证∶四边形 ABCD 是菱形;
(2)若AB=,BD=2,求OE的长.
如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交BC于点F,以DE,EF为邻边作矩形 DEPG,连接CG.
求证∶矩形 DEFG是正方形;
若AB=2,CE =2,求CG的长;
(3)当∠ADE =40°时,求∠EFC的度数.
温馨提示;本试卷共三道大题,满分120分,考试时量90分钟。
一、选择题(本大题共10 个小题,每小题3分,共30分)
1、下列图案中,既是轴对称图形又是中心对称图形的是
2、若△ABC的三边长分别为a、b、c,下列条件中能判断△ABC是直角三角形的有
①∠A=∠B-∠C,②∠A:∠B:∠C=3:4:5,③∠A=90°-∠B,④∠A=∠B=∠C⑤a =(b+c)(b-c),⑥a∶b:c=5∶12∶13.
A.3个 B.4个 C.5个 D.6个
3、点M在第二象限,它到x轴的距离为1,到y轴的距离为2,则点M的坐标是
A.(-2,1) B.(2,-1) C.(1,-2) D.(-1,2)
4、以下列各组数为三角形的三条边长∶①1,,3;②9,40,41;③,,2;④1.5,2.5,2.其中能构成直角三角形的有
A.1 组 B.2组 C.3组 D.4组
5、下列条件中,不能判定两个直角三角形全等的是
A.一个锐角和斜边对应相等B.两条直角边对应相等
C.两个锐角对应相等D.斜边和一直角边对应相等
6、下列说法正确的有
①对角线互相平分的四边形是平行四边形②对角线相等的四边形是矩形
③对角线,互相垂直的四边形是菱形④对角线相等的平行四边形是矩形
⑤对角线互相垂直且相等的平行四边形是正方形
A.1个 B.2个 C.3个 D.4个
7、如图,一根木棍(AB),斜靠在与地面(OM)垂直的墙(OM)上,当木棍A端沿墙下滑,且B端沿地面向右滑行时,AB 的中点P到点O的距离
A.变大力下 B. 变小 C.先变小后变大 D.不变
第7题图 第8题图 第9题图 第10题图
8、如图,下列条件之一能使平行四边形 ABCD是菱形的为
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③B.②③C.③④D.①②③
9、在数学活动课上,小明提出这样一个问题∶如图,∠B=∠C=90°,E是 BC的
中点,DE 平分∠ADC,则下列说法正确的有
①AB//CD;②AE平分∠DAB;③△EBA≌△DCE;④AB+CD=AD;⑤ME⊥DE.
A.2个 B.3个 C.4个 D.5个
10、如图,在四边形ABCD中,AB//DC,AD=BC=5,DC=7,AB=13,点P从点A 出发以3个单位/s的速度沿 AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA 向终点A运动.当四边形 PQBC为平行四边形时,运动时间为
A.4s B.3s C.2s D.1s
二、填空题(本大题共8个小题,每小题3分,共24分)
11、一个多边形的每个外角都等于60°,则它的内角和等于____
12、将点P(2,-3)向右平移2个单位得到点P1点P2,与点P1关于x轴对称,则P2的坐标是
13、已知菱形 ABCD的面积为24cm ,若对角线AC=6cm,则这个菱形的边长为____cm
14、如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为_____
第14题图 第15题图 第16题图
15、如图,矩形纸片ABCD中,AB=4,,BC=6,将ABCD沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于_____
16、如图,□ABCD的对角线AC、BD交于点 O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是__
17、如图,三个边长均为2的正方形重叠在一起,0,02是其中两个正方形的对角线交点,若把这样的n 个小正方形按如图所示方式摆放,则重叠部分的面积为___
18、如图,△A1B1C1,中,A1B1 =4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…以此类推,则第△A2022B2022C2022的周长是_____
解答题(本大题共8个小题,其中第19至25 小题,每题8分;第26小题10分,共66分)
19、(1)某多边形的内角和与外角和的总和为2160°,求此多边形的边数;
(2)某多边形的对角线共有54条,求这个多边形的内角和.
20、如图,∠BAC=90°,BC=28,AC=14,BD=13,AD=15.
(1)求AB的长度;
(2)作DH⊥AB,并求△ADB的面积.
21、在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2;
(3)求△A2B2C2的面积.
22、如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.
求证∶∠EBF= ∠EDF.
23、已知,如图,AABC的中线BE,CF相交于点G,P,Q分别是BC,CG的中点.求证;
(1)四边形 EFPQ是乎行四边形;.
(2)BG=2GE,CG=2GF.
24、在ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证∶四边形 BFDE 是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形 BFDE 的面积
如图,在四边形ABCD中,AB//DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE,
求证∶四边形 ABCD 是菱形;
(2)若AB=,BD=2,求OE的长.
如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交BC于点F,以DE,EF为邻边作矩形 DEPG,连接CG.
求证∶矩形 DEFG是正方形;
若AB=2,CE =2,求CG的长;
(3)当∠ADE =40°时,求∠EFC的度数.
同课章节目录
