4.1.2指数函数的性质与图像 学案(Word版无答案)
文档属性
| 名称 | 4.1.2指数函数的性质与图像 学案(Word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览

文档简介
指数函数的图像和性质
【学习目标】
1. 通过实际例子概括、理解和掌握指数函数的图像和性质。
2. 通过具体例子了解指数函数随底数变化而变化的趋势。
3. 通过练习使学生掌握指数函数图像和性质的简单应用,培养学生应用函数的图像和性质解决问题的能力。
【学习重点】
指数函数的图像和性质。
【学习难点】
指数函数性质的应用。
【学习过程】
养成解题前画图的好习惯:图形是一种直观形象的数学语言,画图可以调动学生的思维活动,加深数学概念的理解与记忆,提高学生的自学能力,提高学习效率,培养学生的空间想象能力,为培养逻辑推理能力打下良好的基础;同时可以使学生很容易从图形中发现解决问题的方法途径;希望同学们在解题前根据具体情况画出适当的图形,坚持每节课画出一个准确的图形。
知识链接:
1.函数﹍﹍﹍﹍﹍﹍﹍﹍﹍叫作指数函数;其定义域是﹍﹍﹍﹍。
2.实数指数幂的三条运算性质是﹍﹍﹍﹍﹍﹍﹍﹍;﹍﹍﹍﹍﹍﹍﹍﹍;﹍﹍﹍﹍﹍﹍﹍其中a>0,b>0。
3.指数函数和图像的相同点是:都位于﹍﹍﹍,都过﹍﹍﹍;不同点是:函数的图像是﹍﹍﹍;函数的图像是﹍﹍﹍﹍。
4.我们通过列表、描点、连线的方法画出、;、 的图像,试比较概括出一般指数函数的图像和性质:
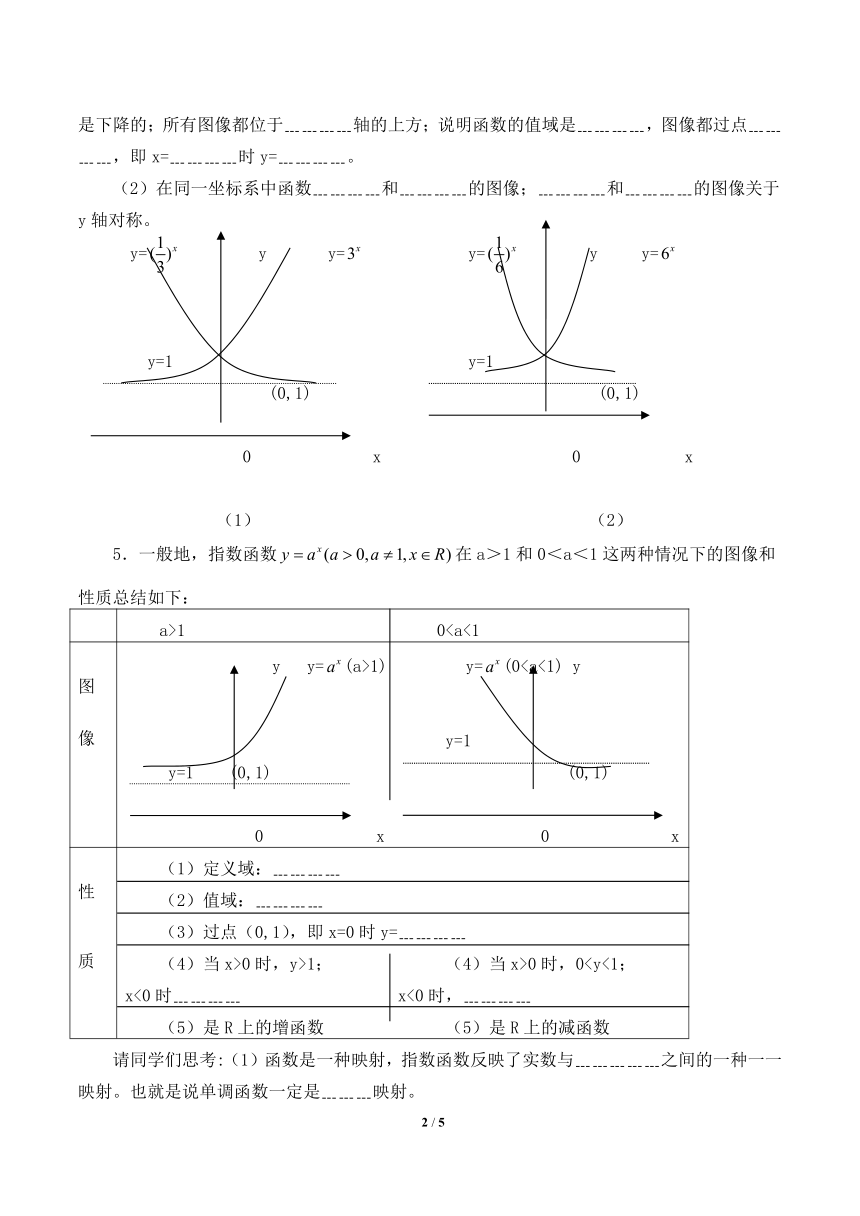
(1)通过观察图像(1)、(2)可知:图像左右延伸无止境,说明函数的定义域是
﹍﹍;﹍﹍﹍﹍和﹍﹍﹍﹍的图像自左向右是上升的;﹍﹍﹍﹍和﹍﹍﹍﹍的图像自左向右是下降的;所有图像都位于﹍﹍﹍﹍轴的上方;说明函数的值域是﹍﹍﹍﹍,图像都过点﹍﹍﹍﹍,即x=﹍﹍﹍﹍时y=﹍﹍﹍﹍。
(2)在同一坐标系中函数﹍﹍﹍﹍和﹍﹍﹍﹍的图像;﹍﹍﹍﹍和﹍﹍﹍﹍的图像关于y轴对称。
y= y y= y= y y=
y=1 y=1
(0,1) (0,1)
0 x 0 x
(1) (2)
5.一般地,指数函数在a>1和0<a<1这两种情况下的图像和性质总结如下:
a>1 0图 像 y y=(a>1) y=(0性 质 (1)定义域:﹍﹍﹍﹍(2)值域:﹍﹍﹍﹍ (3)过点(0,1),即x=0时y=﹍﹍﹍﹍(4)当x>0时,y>1; (4)当x>0时,0请同学们思考:(1)函数是一种映射,指数函数反映了实数与﹍﹍﹍﹍﹍之间的一种一一映射。也就是说单调函数一定是﹍﹍﹍映射。
(2)当函数y=与函数y=(即函数y=)的自变量的取值互为相反数时,其函数值是相等的,这两个函数的图像是关于﹍﹍﹍﹍轴对称的。
一、基础练习:
(C级)1.利用指数函数的性质,比较下列各题中两个数的大小(请写出过程):
(1); (2)。
(C级)2.(1)求使不等式成立的x的集合;(2)已知,求数a的取值范围。
二、自我检测:
(C级)(1)利用指数函数的性质比较下列两个数的大小:
1 ; ②。
(C级)(2)已知-1(C级)(3)设f(x)=,求证:(1)f(x)·f(y)=f(x+y);(2)f(x)÷f(y)=f(x-y)
能力提升:
(D级)1.在同一直角坐标系中作出下列函数的图像,讨论它们之间的关系:
(1); (2)。
因此,可得以下结论:一般地,
①当a>b>1时,指数的函数图像恒过(0,1)点,即x=0时;x<0时,有;x>0时,有;其底数越大,x>0时其函数值增长越﹍﹍﹍﹍。
②当00时,有;x<0时,有;其底数越小,x>0时其函数值减小越﹍﹍﹍﹍。
(D级)2.已知,比较,,的大小。
【作业布置】
(C级)1.求下列函数中自变量x的取值范围:
(1); (2); (3) y=; (4)y=。
(选作题D级)2.在同一直角坐标系中画出下列函数的图像,讨论它们之间的联系:
(1); (2)。
PAGE
5 / 5
【学习目标】
1. 通过实际例子概括、理解和掌握指数函数的图像和性质。
2. 通过具体例子了解指数函数随底数变化而变化的趋势。
3. 通过练习使学生掌握指数函数图像和性质的简单应用,培养学生应用函数的图像和性质解决问题的能力。
【学习重点】
指数函数的图像和性质。
【学习难点】
指数函数性质的应用。
【学习过程】
养成解题前画图的好习惯:图形是一种直观形象的数学语言,画图可以调动学生的思维活动,加深数学概念的理解与记忆,提高学生的自学能力,提高学习效率,培养学生的空间想象能力,为培养逻辑推理能力打下良好的基础;同时可以使学生很容易从图形中发现解决问题的方法途径;希望同学们在解题前根据具体情况画出适当的图形,坚持每节课画出一个准确的图形。
知识链接:
1.函数﹍﹍﹍﹍﹍﹍﹍﹍﹍叫作指数函数;其定义域是﹍﹍﹍﹍。
2.实数指数幂的三条运算性质是﹍﹍﹍﹍﹍﹍﹍﹍;﹍﹍﹍﹍﹍﹍﹍﹍;﹍﹍﹍﹍﹍﹍﹍其中a>0,b>0。
3.指数函数和图像的相同点是:都位于﹍﹍﹍,都过﹍﹍﹍;不同点是:函数的图像是﹍﹍﹍;函数的图像是﹍﹍﹍﹍。
4.我们通过列表、描点、连线的方法画出、;、 的图像,试比较概括出一般指数函数的图像和性质:
(1)通过观察图像(1)、(2)可知:图像左右延伸无止境,说明函数的定义域是
﹍﹍;﹍﹍﹍﹍和﹍﹍﹍﹍的图像自左向右是上升的;﹍﹍﹍﹍和﹍﹍﹍﹍的图像自左向右是下降的;所有图像都位于﹍﹍﹍﹍轴的上方;说明函数的值域是﹍﹍﹍﹍,图像都过点﹍﹍﹍﹍,即x=﹍﹍﹍﹍时y=﹍﹍﹍﹍。
(2)在同一坐标系中函数﹍﹍﹍﹍和﹍﹍﹍﹍的图像;﹍﹍﹍﹍和﹍﹍﹍﹍的图像关于y轴对称。
y= y y= y= y y=
y=1 y=1
(0,1) (0,1)
0 x 0 x
(1) (2)
5.一般地,指数函数在a>1和0<a<1这两种情况下的图像和性质总结如下:
a>1 0
(2)当函数y=与函数y=(即函数y=)的自变量的取值互为相反数时,其函数值是相等的,这两个函数的图像是关于﹍﹍﹍﹍轴对称的。
一、基础练习:
(C级)1.利用指数函数的性质,比较下列各题中两个数的大小(请写出过程):
(1); (2)。
(C级)2.(1)求使不等式成立的x的集合;(2)已知,求数a的取值范围。
二、自我检测:
(C级)(1)利用指数函数的性质比较下列两个数的大小:
1 ; ②。
(C级)(2)已知-1
能力提升:
(D级)1.在同一直角坐标系中作出下列函数的图像,讨论它们之间的关系:
(1); (2)。
因此,可得以下结论:一般地,
①当a>b>1时,指数的函数图像恒过(0,1)点,即x=0时;x<0时,有;x>0时,有;其底数越大,x>0时其函数值增长越﹍﹍﹍﹍。
②当0
(D级)2.已知,比较,,的大小。
【作业布置】
(C级)1.求下列函数中自变量x的取值范围:
(1); (2); (3) y=; (4)y=。
(选作题D级)2.在同一直角坐标系中画出下列函数的图像,讨论它们之间的联系:
(1); (2)。
PAGE
5 / 5
