沪科版七年级下册 8.1 幂的运算 课件(共37张PPT)
文档属性
| 名称 | 沪科版七年级下册 8.1 幂的运算 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 270.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 07:02:20 | ||
图片预览










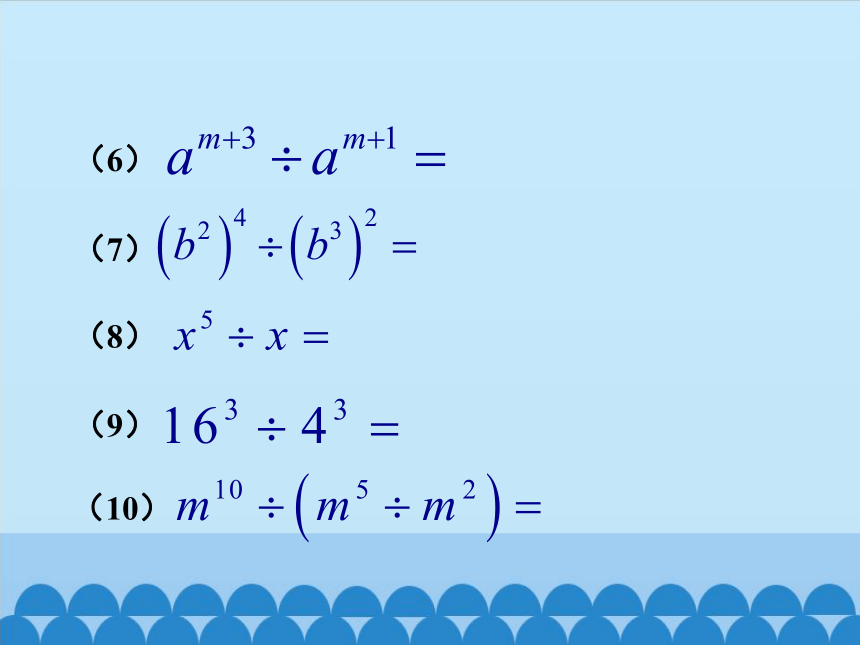

文档简介
(共37张PPT)
同底数幂的除法
幂的运算
我们在前面学习了幂的有关运算性质,这些运算都有哪些?
1.同底数幂相乘,底数不变,指数相加。
2.幂的乘方,底数不变,指数相乘。
3.积的乘方,等于每一个因式乘方的积 。
一、温故知新
1.试一试
用你熟悉的方法计算:
二、探索同底数幂除法法则
2.概括
你们能发现什么规律?
一般地,设m、n为正整数,m>n, ,有
这就是说,同底数幂相除,底数不变,指数相减。
am÷an=
=
=am-n
m个a
n个a
(m-n)个a
3.典型例题
例 计算
(1)
(2)
(3)
(4)
解:
(1)
(2)解:
(3)解:
(4)解:
例 计算
(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
例 计算
解:
例 计算
(1)
(2)
分析:本例的每个小题,由于底数不同,不能直接运用同底数幂的除法法则计算,但可以先利用其他的幂的运算法则转化为同底数幂的情况,再进行除法运算。
解:(1)
解:(2)
三、练习:
1.填空:
(1)
(2)
(3)
(4)
(5)(a-b)5÷(b-a)4
(7)
(6)
(9)
(10)
(8)
2.选择
下面运算正确的是( )
B.
C.
D.
A.
3.已知: , ,
求:
不要把 的指数误认为是0。
四、小结:
(1)运用法则的关键是看底数是否相同;
(2)因为零不能作除数,所以底数不能为0;
(3)注意单个字母的指数为1,如
温故知新
我们在前面学习了幂的有关运算性质,这些运算都有哪些?
1.同底数幂相乘,底数不变,指数相加。
2.幂的乘方,底数不变,指数相乘。
3.积的乘方,等于每一个因式乘方的积。
4.同底数幂相除,底数不变,指数相减。
( 且m>n )
那么当 时呢?
合作探究
1.根据除法运算中,一个数除以它本身商为1,得
33÷33=1;108÷108=1;an÷an=1(a≠0)
若按同底数幂的除法性质,得
33÷33= ;108÷108= ;
an÷an= (a≠0)
于是约定:a0=1(a≠0)
语言表述:任何一个不等于零的数的零指数幂等于1。
33-3=30
108-8=100
an-n=a0
结论:30=1,100=1,a0=1(a≠0)
2.根据同底数幂相乘,除法运算及分数约分,得:
根据同底数幂的除法运算,得:
32÷35=32-5=3-3;104÷108=104-8=10-4;am÷an=am-n=a-p
于是约定:
语言叙述:任何一个不等于零的数的-p(p为正整数)
指数幂,等于这个数的p指数幂的倒数。
结论:
3.计算:
例5计算:
巩固新知:
练习:课本习题
课堂小结:
通过本节课学习,你有什么收获?
作业:
课堂作业:必做题:课本习题
选做题:计算:
家庭作业:练习册
,求x的值。
合作探究:
1.一般地,一个绝对值大于或等于10的数都可记成±a×10n的形式,其中1≤a<10,n等于原数的整数位数减1。这种记数方法叫做科学记数法。
2.用“科学记数法”表示:354000、186400000、
35亿、1300万
解:354000=
186400000=
35亿=
1300万=
3.54×105
1.864×108
3.5×109
1.3×107
3.用分数表示: 4.把0.1、0.01、0.001、
表示成分数
10-1、10-2、10-3
解:
解:
你能看出它们的关系吗?
=10-1
=10-2
=10-3
由上面的探究可得:
由此可见,绝对值小于1的数也可以表示成±a×10n的形式。
我知道了:
1个绝对值很小的数可以写成只有1个一位整数与10的负整数指数幂的积的形式。以前用科学记数法表示一个绝对值很大的数,现在还可以用科学记数法表示一个绝对值很小的数。
一般地,一个绝对值很大或很小的数都可以利用科学记数法写成±a×10n的形式,其中1≤a<10,n是整数。
例题剖析:
例6 用科学记数法表示下列各数:
(1)0.00076 (2)-0.00000159
(3)0.0000283
解:0.00076=7.6×0.0001=7.6×10-4
-0.00000159=-1.59×0.000001=-1.59×10-6
0.0000283=2.83×0.00001=2.83×10-5
归纳:
用科学记数法表示一个绝对值较小的数时,数n就等于这个数的第一个不为零的有效数字前面零的个数(包括小数点前面的零)
人体中红细胞的直径约为0.000 0077m,而流感病毒的直径约为0.000 000 08m,用科学记数法表示这两个量。
解:0.000 0077m=7.7×10-6m
0.000 000 08m=8×10-8m
规律
小数点向右移几位,指数就是负几。
“纳米”已经进入了社会生活的方方面面(如纳米食品、纳米衣料…)
(1)你听说过“纳米”吗?
(2)知道“纳米”是什么吗?
(纳米是一个长度单位)
(3)1“纳米”有多长?
(1nm=十亿分之一m)
(4)纳米记为nm,请你用科学记数法表示1 nm等于多少米?5nm呢?18nm呢?
10-9m
1nm=0.000000001m=
5nm=5×10-9m 18nm=1.8×10-8m
1.用科学记数法表示下列各数:
(1)0.000 0032=
(2)-0.000 00014=
(3)-680 000 000=
(4)314 000 000 000=
3.2×10-6
-1.4×10-7
-6.8×108
3.14×1011
2.写出下列用科学记数法表示的数的原来的数。
(1)2.718×106=
(2)-1.414×10-4=
2718000
-0.0001414
3.填空:
(1)若67 950 000=6.795×10m,
则m= ;
(2)若0.000 010 2=1.02×10n,
则n= 。
7
-5
4.计算:
4×1011×4.13×10-17
(结果用小数表示)
5.课本练习
(0.00001652)
布置作业
课堂:必做:练习题。
选作:已知:xm=2,xn=3,求 x3m-2n。
家庭:习题 练习册
谢 谢
同底数幂的除法
幂的运算
我们在前面学习了幂的有关运算性质,这些运算都有哪些?
1.同底数幂相乘,底数不变,指数相加。
2.幂的乘方,底数不变,指数相乘。
3.积的乘方,等于每一个因式乘方的积 。
一、温故知新
1.试一试
用你熟悉的方法计算:
二、探索同底数幂除法法则
2.概括
你们能发现什么规律?
一般地,设m、n为正整数,m>n, ,有
这就是说,同底数幂相除,底数不变,指数相减。
am÷an=
=
=am-n
m个a
n个a
(m-n)个a
3.典型例题
例 计算
(1)
(2)
(3)
(4)
解:
(1)
(2)解:
(3)解:
(4)解:
例 计算
(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
例 计算
解:
例 计算
(1)
(2)
分析:本例的每个小题,由于底数不同,不能直接运用同底数幂的除法法则计算,但可以先利用其他的幂的运算法则转化为同底数幂的情况,再进行除法运算。
解:(1)
解:(2)
三、练习:
1.填空:
(1)
(2)
(3)
(4)
(5)(a-b)5÷(b-a)4
(7)
(6)
(9)
(10)
(8)
2.选择
下面运算正确的是( )
B.
C.
D.
A.
3.已知: , ,
求:
不要把 的指数误认为是0。
四、小结:
(1)运用法则的关键是看底数是否相同;
(2)因为零不能作除数,所以底数不能为0;
(3)注意单个字母的指数为1,如
温故知新
我们在前面学习了幂的有关运算性质,这些运算都有哪些?
1.同底数幂相乘,底数不变,指数相加。
2.幂的乘方,底数不变,指数相乘。
3.积的乘方,等于每一个因式乘方的积。
4.同底数幂相除,底数不变,指数相减。
( 且m>n )
那么当 时呢?
合作探究
1.根据除法运算中,一个数除以它本身商为1,得
33÷33=1;108÷108=1;an÷an=1(a≠0)
若按同底数幂的除法性质,得
33÷33= ;108÷108= ;
an÷an= (a≠0)
于是约定:a0=1(a≠0)
语言表述:任何一个不等于零的数的零指数幂等于1。
33-3=30
108-8=100
an-n=a0
结论:30=1,100=1,a0=1(a≠0)
2.根据同底数幂相乘,除法运算及分数约分,得:
根据同底数幂的除法运算,得:
32÷35=32-5=3-3;104÷108=104-8=10-4;am÷an=am-n=a-p
于是约定:
语言叙述:任何一个不等于零的数的-p(p为正整数)
指数幂,等于这个数的p指数幂的倒数。
结论:
3.计算:
例5计算:
巩固新知:
练习:课本习题
课堂小结:
通过本节课学习,你有什么收获?
作业:
课堂作业:必做题:课本习题
选做题:计算:
家庭作业:练习册
,求x的值。
合作探究:
1.一般地,一个绝对值大于或等于10的数都可记成±a×10n的形式,其中1≤a<10,n等于原数的整数位数减1。这种记数方法叫做科学记数法。
2.用“科学记数法”表示:354000、186400000、
35亿、1300万
解:354000=
186400000=
35亿=
1300万=
3.54×105
1.864×108
3.5×109
1.3×107
3.用分数表示: 4.把0.1、0.01、0.001、
表示成分数
10-1、10-2、10-3
解:
解:
你能看出它们的关系吗?
=10-1
=10-2
=10-3
由上面的探究可得:
由此可见,绝对值小于1的数也可以表示成±a×10n的形式。
我知道了:
1个绝对值很小的数可以写成只有1个一位整数与10的负整数指数幂的积的形式。以前用科学记数法表示一个绝对值很大的数,现在还可以用科学记数法表示一个绝对值很小的数。
一般地,一个绝对值很大或很小的数都可以利用科学记数法写成±a×10n的形式,其中1≤a<10,n是整数。
例题剖析:
例6 用科学记数法表示下列各数:
(1)0.00076 (2)-0.00000159
(3)0.0000283
解:0.00076=7.6×0.0001=7.6×10-4
-0.00000159=-1.59×0.000001=-1.59×10-6
0.0000283=2.83×0.00001=2.83×10-5
归纳:
用科学记数法表示一个绝对值较小的数时,数n就等于这个数的第一个不为零的有效数字前面零的个数(包括小数点前面的零)
人体中红细胞的直径约为0.000 0077m,而流感病毒的直径约为0.000 000 08m,用科学记数法表示这两个量。
解:0.000 0077m=7.7×10-6m
0.000 000 08m=8×10-8m
规律
小数点向右移几位,指数就是负几。
“纳米”已经进入了社会生活的方方面面(如纳米食品、纳米衣料…)
(1)你听说过“纳米”吗?
(2)知道“纳米”是什么吗?
(纳米是一个长度单位)
(3)1“纳米”有多长?
(1nm=十亿分之一m)
(4)纳米记为nm,请你用科学记数法表示1 nm等于多少米?5nm呢?18nm呢?
10-9m
1nm=0.000000001m=
5nm=5×10-9m 18nm=1.8×10-8m
1.用科学记数法表示下列各数:
(1)0.000 0032=
(2)-0.000 00014=
(3)-680 000 000=
(4)314 000 000 000=
3.2×10-6
-1.4×10-7
-6.8×108
3.14×1011
2.写出下列用科学记数法表示的数的原来的数。
(1)2.718×106=
(2)-1.414×10-4=
2718000
-0.0001414
3.填空:
(1)若67 950 000=6.795×10m,
则m= ;
(2)若0.000 010 2=1.02×10n,
则n= 。
7
-5
4.计算:
4×1011×4.13×10-17
(结果用小数表示)
5.课本练习
(0.00001652)
布置作业
课堂:必做:练习题。
选作:已知:xm=2,xn=3,求 x3m-2n。
家庭:习题 练习册
谢 谢
