物理人教版(2019)选择性必修第一册1.2动量定理(共27张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.2动量定理(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-06 10:50:46 | ||
图片预览






文档简介
(共27张PPT)
第一章 动量守恒定律
1.2 动量定理
温故知新
由动能定理可知:动能的变化是由于合力做功而改变。
加速度是由物体所受的合外力产生的。
那么,动量的变化又是什么原因引起的呢?
动量的变化由速度的变化导致
速度的变化是因为有加速度
也是等于合力所做功吗?
光滑水平面上物体在水平恒力F作用下,经过一段时间t,动量的变化如何?
解:Δp=mv2-mv1=mΔv
加速度定义:Δv=aΔt
据牛顿第二定律: a=F/m
得:(1)Δp=FΔt
(2)F=Δp/Δt
力是产生加速度的原因,力也称作动量变化率。合力越大动量变化越快。
表明动量的变化决定于合力与合力作用时间的乘积
动量的变化决定因素
1. 定义:某力的冲量为该力和该力作用时间的乘积。
3.单位:在国际单位制中,冲量的单位是牛·秒,符号是N·s
4.方向:冲量为矢量,力的冲量的方向跟该力的方向相同
2.表达式:I=Ft(使用该式计算时,F必须为恒力)
一、冲 量
5.F-t图像面积意义:反映了力对物体冲量,且有正负面积之分。
注意:有力作用于物体,该力一定产生冲量,但不一定做功;力对物体做了功,一定有冲量。
冲量 功
区别 意义
公式
单位
标、矢量
正负
作用效果
联系
二、冲 量与功的比较
改变物体的动量
改变物体的动能
W=Fxcos θ
I=Ft
力在时间上的累积, 对应一段时间
在F-t图像中可以用面积表示
力在位移上累积, 对应一段位移
在F-x图像中可以用面积表示
N·S
N·m(J)
矢量
标量
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
有力作用,一定有冲量;不一定做功
三、合力的冲量的求值
1.运算法则:冲量为矢量,遵守平行四边形定则(与求总功不同)。
2.求合力冲量方法:(与求合力方法类似)
(1)多力共线时,可以直接代数运算I合=I1+I2+......(主要运算方式)
(2)多力互成夹角时,先求I1、I2、I3,然后矢量合成
若各力作用时间相同,且合力为恒力,则I=F合t
①两力的合力冲量,直接合成(先确定方向,再合成)
②两力以上,先正交分解再合成
【例题1】质量为m的物体放在水平地面上,在与水平面成 角的拉力F作用下由静止开始运动,经时间t速度达到v,在这段时间内拉力F和重力mg冲量大小分别是 ( )
A.Ft,0 B.Ftcos , 0
C.mv, 0 D.Ft, mgt
D
有力作用,一定有冲量;不一定做功
【例题2】如图所示,质量为m=1kg的物块在倾角为37°的光滑斜面顶端上由静止下滑,斜面长为12m,求物块下滑到斜面底端过程中
(1)支持力的冲量
(2)重力的冲量
(3)合外力的冲量.
功为标量,各力无论共线或成夹角,总功总有:W总=W1+W2+......
冲量为矢量,各力成一定夹角时,总冲量I合≠I1+I2+.......;
四、变力冲量的计算
1. 平均力法:当力的方向不变,大小随时间t(不是随位移x)均匀变化时,则力F在时间上的平均值F平均=(F1十F2)/2,再由I=F平均t 计算冲量。
2.F-t图像面积法:F -t图线与t轴所围的面积等于力F冲量的数值。上方面积取正值,表示正向冲量;下方面积为负值,代表反向冲量.总冲量为I总=S1+S2+......
3.动量定理法:所有变力的冲量通常是借助于动量定理来计算的。
光滑水平面上质量为m的物体在水平恒力作用下,经过一段时间,速度由v1增加到v2,求合力的冲量I
解:I合=IF=F合t
加速度定义:a=Δv/Δt=(v2-v1)/Δt
得:I合=mv2-mv1=Δp
动量定理的推导
据牛顿第二定律: F合=ma
1、内容:物体所受合外力的冲量等于物体的动量变化。
2、表达式:I合=Δp
五、动量定理
①I1+I2=mv2-mv1
②F合Δt=mv2-mv1
3、理解:
(1)I合=Δp 合外力的冲量(不是某个力的冲量)是动量变化的原因;
所有刚性碰撞、爆炸瞬间,I合≈ I冲击力,可忽略重力
(4)矢量式,使用时要先规定正方向,一般以初速度方向为正方向
(2)I1+I2=mv2-mv1 :I1、I2共线时,I合=I1+I2 ; v1、v2共线时,Δp=mv2-mv1
(3)F合Δt=mv2-mv1 : F合为恒力 ; v1、v2共线时Δp=mv2-mv1
(5)求冲量和动量变化的两种方法:直接公式法和间接动量定理法
4.动量定理的应用:I合=Δp即:I1+I2=I变+F恒t=mv2-mv1
(1)动量定理既可求恒力F,也可求变力F,对于变力,动量定理中
的F应理解为变力在作用时间内的平均值;
(2) 既可求恒力冲量I,也可求变力冲量I;还可求恒力作用时间。
(3)动量定理不仅可以解决匀变速直线的初末速度v、还可以解决曲线运动和非匀变速的的初末速度v。
(4)动量定理不仅适用于宏观低速物体,也适用于微观高速运动。
(5)三大观点对比:
①和牛顿运动定律相比,不考虑中间过程,只考虑初末状态。
②和动能定理相比,可求时间和冲量,不能求位移和路程和功
但都不能求加速度。
动量定理解释生活现象
4.F合Δt=Δp公式中F合、Δt、Δp关系:
(1)Δp一定,F与t成反比, 作用时间t越长,则F合越小.
(2)F一定,Δp与t成正比,作用时间t越长,则Δp越大.
(3)t一定,Δp与F成正比,F合越大,则Δp越大
跳高比赛中为什么要垫海绵垫?
与直接落在地面上什么相同?什么不同?
增大运动员落地减速过程的作用时间,减小冲击力
动量变化Δp相同,减速过程作用时间Δt不同,合力F合不同,冲击力F不同
木块合力F合相同,加速过程作用时间Δt不同,动量变化Δp不相同
迅速和缓慢抽出纸带什么相同?什么不同?
【例题1】 一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间 为0.01s。球棒对垒球的平均作用力是多大?
解:以初速度方向为正方向
末动量为
p2=mv2= - 8.1kg·m/s
由动量定理知
负号表示力的方向与初速度方向相反
p1=mv1=4.5kg·m/s
注意:作用时间极短的碰撞模式中受力分析时,一般有重力远小于冲击力,可忽略重力冲量
初动量为
(1)落地时vy2=2gh=10m/s
所以v=√v02+vy2=10√2m/s
则P=mv=10√2kgm/s,
(2)Δp=√p2-p02=10kgm/s,
【例题2】一个质量为 1 kg 的物体从距地面高为h=5m处以v0=10m/s的水平初速度抛出g=10m/s2.求:
(1)落地时动量
(2) 下落过程中动量的变化量
解:
(1)初末动量不共线时,动量变化只能矢量运算
(2)求动量、动量变化、冲量时,要作方向说明
与水平地面成夹角45°
方向竖直向下
【例题3】在撑竿跳比赛的横杆下方要放上很厚的海绵垫子.设一位撑竿跳运动员的质量为70 kg,越过横杆后从h=5.6 m高处落下,落在海绵垫上经历时间Δt=1 s停下.求海绵垫对运动员的作用力.(g=10m/s2)
解:下落到静止,以竖直向下为正方向
据动量定理可知:IG+IF=ΔP=0 ---①
自由落体过程:h=gt2/2 ---②
即:mg(t+Δt)+FΔt=0 ---③
代入数据解①②③得:F=-1441N,方向竖直向上
(1)多过程可全程立式求解
(2)动量的变化等于合力的冲量,不是某一个力的冲量
(3)多力共线时,合力冲量时可直接代数运算
【例题4】2020年11月24日,中国用长征五号运载火箭成功发射嫦娥五号探测器,并将其送入预定轨道,运载火箭点火时向下喷气,会对地面产生冲击力。假设火箭喷气口的横截面积为S,喷出气体的速度为v(相对于地面),气体垂直射向地面后竖直速度变为零。已知气体的密度为ρ,重力加速度大小为g,则气体对地面的平均冲击力
解:以气体初速度方向为正方向
据动量定理可知FΔt=ΔP=-Δmv---①
Δt内经过S的气体质量
Δm=ρV=ρvΔtS---②
解①②得F=-ΔP/Δt=-ρSv2
根据牛顿第三定律可知:
气体对地面的冲击力F'=-F=ρSv2
方向竖直向下
v
F
S
动量定理的应用步骤
1、确定研究对象、物理过程,规定正方向
4、根据动量定理列方程,统一单位后代入数据求解。
2、正确受力分析、冲量分析(是否共线),求合外力冲量;
3、初末状态分析,确定初末状态即初末动量;
典型例题
对课后习题进行详细分析,并在此基础之上进行思考和总结。
1、下列说法中正确的是( )
A、冲量是反映力的作用时间积累效果的物理量
B、合力越大,动量变化越大
C、冲量是物体动量变化的原因
D、合力冲量越大,动量变化越大
ACD
课堂练习
2、甲、乙两个质量相同的物体,以相同的初速度分别在粗糙程度不同的水平面上运动,乙物体先停下来,甲物体又经较长时间停下来,下面叙述中正确的是( )
A、甲物体受到的冲量大
B、乙物体受到的冲量大
C、两个物体受到的冲量大小相等
D、无法判断
C
3、某物体做匀变速直线运动,初始动能为E,经过一段时间后速度增加量为2v,动能增加量为3E,则这段时间内物体的动量变化为( )
A. E/2v B. E/v C. 2E/v D. 3E/2v
B
4、 如图所示,用高压水枪喷出的强力水柱冲击右侧的煤层.设水柱直径为 D,水流速度为v,方向水平,水柱垂直于煤层表面,水柱冲击煤层后水的速度为零.手持高压水枪进行操作,进入水枪的水流速度可忽略不计,已知水的密度为 p.下列说法正确的是( )
A. 高压水枪单位时间喷出的水的质量为ρπvD2
B. 高压水枪的功率为ρπD2v3/8
C. 水柱对煤层的平均冲力为ρπD2v2/4·
D. 手对高压水枪的作用力水平向右
BC
5、某游乐园有一喷泉,在水泵作用喷出竖直向上的水柱,将站在冲浪板上的玩偶模型托起,悬停在空中,这一景观可做如下简化,假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出,冲浪板底部为平板且其面积大于水柱的横截面积,保证所有水都能喷到冲浪板的底部。冲击冲浪板后,水在竖直方向的速度立即变为零,已知玩偶模型和冲浪板的总质量为M,水的密度为ρ,重力加速度大小为g,空气阻力及水的粘滞阻力均可忽略不计。
(1)计算玩偶模型在空中悬停时水对冲浪板的冲击力大小
(2)求喷泉单位时间内喷出的水的质量;
(3)求玩偶模型在空中悬停时,冲浪板的底面相对于喷口的高度。
答案 (1)Mg (2)ρv0S
解:(1)模型静止时,据二力平衡可知:F=Mg
(2)Δt内, 喷出水的体积为:ΔV=v0SΔt
质量为:Δm=ρΔV,
单位时间内质量为:m=Δm/Δt=ρv0S
(3)设高度为h,从喷出到板底过程:
据动量定理有:F·Δt=Δp ---②
解①②得:
---①
(忽略水柱微元重力的冲量)
谢谢 再见!
第一章 动量守恒定律
1.2 动量定理
温故知新
由动能定理可知:动能的变化是由于合力做功而改变。
加速度是由物体所受的合外力产生的。
那么,动量的变化又是什么原因引起的呢?
动量的变化由速度的变化导致
速度的变化是因为有加速度
也是等于合力所做功吗?
光滑水平面上物体在水平恒力F作用下,经过一段时间t,动量的变化如何?
解:Δp=mv2-mv1=mΔv
加速度定义:Δv=aΔt
据牛顿第二定律: a=F/m
得:(1)Δp=FΔt
(2)F=Δp/Δt
力是产生加速度的原因,力也称作动量变化率。合力越大动量变化越快。
表明动量的变化决定于合力与合力作用时间的乘积
动量的变化决定因素
1. 定义:某力的冲量为该力和该力作用时间的乘积。
3.单位:在国际单位制中,冲量的单位是牛·秒,符号是N·s
4.方向:冲量为矢量,力的冲量的方向跟该力的方向相同
2.表达式:I=Ft(使用该式计算时,F必须为恒力)
一、冲 量
5.F-t图像面积意义:反映了力对物体冲量,且有正负面积之分。
注意:有力作用于物体,该力一定产生冲量,但不一定做功;力对物体做了功,一定有冲量。
冲量 功
区别 意义
公式
单位
标、矢量
正负
作用效果
联系
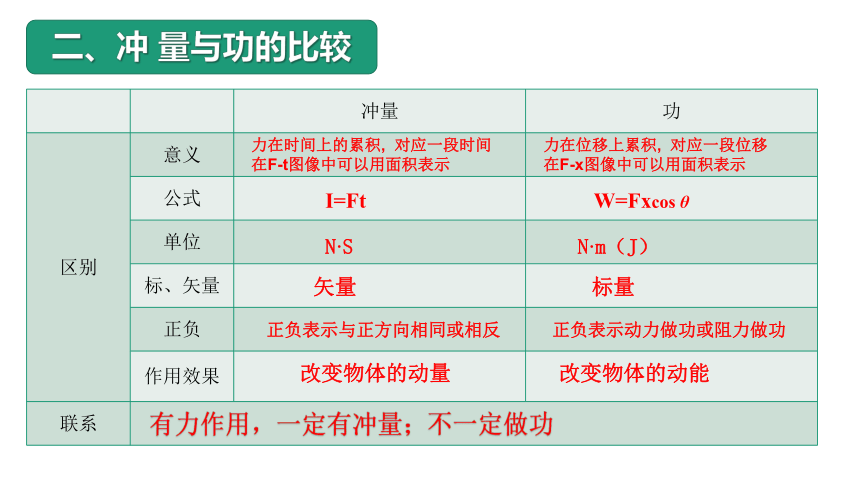
二、冲 量与功的比较
改变物体的动量
改变物体的动能
W=Fxcos θ
I=Ft
力在时间上的累积, 对应一段时间
在F-t图像中可以用面积表示
力在位移上累积, 对应一段位移
在F-x图像中可以用面积表示
N·S
N·m(J)
矢量
标量
正负表示与正方向相同或相反
正负表示动力做功或阻力做功
有力作用,一定有冲量;不一定做功
三、合力的冲量的求值
1.运算法则:冲量为矢量,遵守平行四边形定则(与求总功不同)。
2.求合力冲量方法:(与求合力方法类似)
(1)多力共线时,可以直接代数运算I合=I1+I2+......(主要运算方式)
(2)多力互成夹角时,先求I1、I2、I3,然后矢量合成
若各力作用时间相同,且合力为恒力,则I=F合t
①两力的合力冲量,直接合成(先确定方向,再合成)
②两力以上,先正交分解再合成
【例题1】质量为m的物体放在水平地面上,在与水平面成 角的拉力F作用下由静止开始运动,经时间t速度达到v,在这段时间内拉力F和重力mg冲量大小分别是 ( )
A.Ft,0 B.Ftcos , 0
C.mv, 0 D.Ft, mgt
D
有力作用,一定有冲量;不一定做功
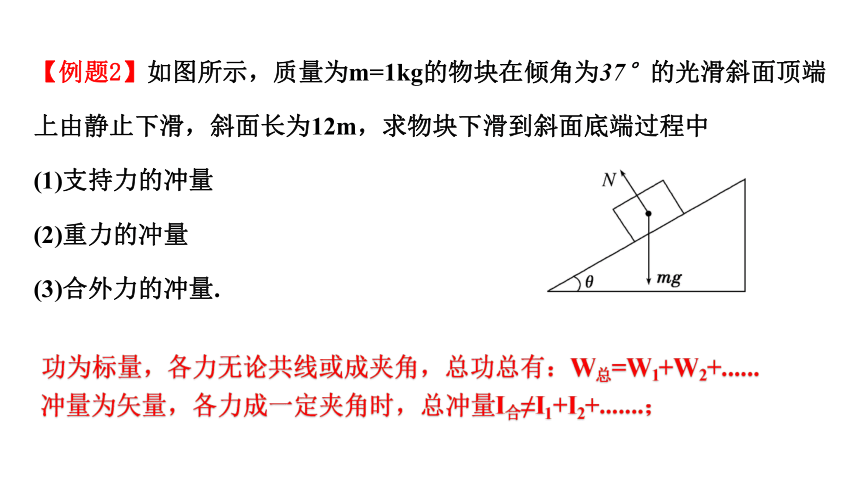
【例题2】如图所示,质量为m=1kg的物块在倾角为37°的光滑斜面顶端上由静止下滑,斜面长为12m,求物块下滑到斜面底端过程中
(1)支持力的冲量
(2)重力的冲量
(3)合外力的冲量.
功为标量,各力无论共线或成夹角,总功总有:W总=W1+W2+......
冲量为矢量,各力成一定夹角时,总冲量I合≠I1+I2+.......;
四、变力冲量的计算
1. 平均力法:当力的方向不变,大小随时间t(不是随位移x)均匀变化时,则力F在时间上的平均值F平均=(F1十F2)/2,再由I=F平均t 计算冲量。
2.F-t图像面积法:F -t图线与t轴所围的面积等于力F冲量的数值。上方面积取正值,表示正向冲量;下方面积为负值,代表反向冲量.总冲量为I总=S1+S2+......
3.动量定理法:所有变力的冲量通常是借助于动量定理来计算的。
光滑水平面上质量为m的物体在水平恒力作用下,经过一段时间,速度由v1增加到v2,求合力的冲量I
解:I合=IF=F合t
加速度定义:a=Δv/Δt=(v2-v1)/Δt
得:I合=mv2-mv1=Δp
动量定理的推导
据牛顿第二定律: F合=ma
1、内容:物体所受合外力的冲量等于物体的动量变化。
2、表达式:I合=Δp
五、动量定理
①I1+I2=mv2-mv1
②F合Δt=mv2-mv1
3、理解:
(1)I合=Δp 合外力的冲量(不是某个力的冲量)是动量变化的原因;
所有刚性碰撞、爆炸瞬间,I合≈ I冲击力,可忽略重力
(4)矢量式,使用时要先规定正方向,一般以初速度方向为正方向
(2)I1+I2=mv2-mv1 :I1、I2共线时,I合=I1+I2 ; v1、v2共线时,Δp=mv2-mv1
(3)F合Δt=mv2-mv1 : F合为恒力 ; v1、v2共线时Δp=mv2-mv1
(5)求冲量和动量变化的两种方法:直接公式法和间接动量定理法
4.动量定理的应用:I合=Δp即:I1+I2=I变+F恒t=mv2-mv1
(1)动量定理既可求恒力F,也可求变力F,对于变力,动量定理中
的F应理解为变力在作用时间内的平均值;
(2) 既可求恒力冲量I,也可求变力冲量I;还可求恒力作用时间。
(3)动量定理不仅可以解决匀变速直线的初末速度v、还可以解决曲线运动和非匀变速的的初末速度v。
(4)动量定理不仅适用于宏观低速物体,也适用于微观高速运动。
(5)三大观点对比:
①和牛顿运动定律相比,不考虑中间过程,只考虑初末状态。
②和动能定理相比,可求时间和冲量,不能求位移和路程和功
但都不能求加速度。
动量定理解释生活现象
4.F合Δt=Δp公式中F合、Δt、Δp关系:
(1)Δp一定,F与t成反比, 作用时间t越长,则F合越小.
(2)F一定,Δp与t成正比,作用时间t越长,则Δp越大.
(3)t一定,Δp与F成正比,F合越大,则Δp越大
跳高比赛中为什么要垫海绵垫?
与直接落在地面上什么相同?什么不同?
增大运动员落地减速过程的作用时间,减小冲击力
动量变化Δp相同,减速过程作用时间Δt不同,合力F合不同,冲击力F不同
木块合力F合相同,加速过程作用时间Δt不同,动量变化Δp不相同
迅速和缓慢抽出纸带什么相同?什么不同?
【例题1】 一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间 为0.01s。球棒对垒球的平均作用力是多大?
解:以初速度方向为正方向
末动量为
p2=mv2= - 8.1kg·m/s
由动量定理知
负号表示力的方向与初速度方向相反
p1=mv1=4.5kg·m/s
注意:作用时间极短的碰撞模式中受力分析时,一般有重力远小于冲击力,可忽略重力冲量
初动量为
(1)落地时vy2=2gh=10m/s
所以v=√v02+vy2=10√2m/s
则P=mv=10√2kgm/s,
(2)Δp=√p2-p02=10kgm/s,
【例题2】一个质量为 1 kg 的物体从距地面高为h=5m处以v0=10m/s的水平初速度抛出g=10m/s2.求:
(1)落地时动量
(2) 下落过程中动量的变化量
解:
(1)初末动量不共线时,动量变化只能矢量运算
(2)求动量、动量变化、冲量时,要作方向说明
与水平地面成夹角45°
方向竖直向下
【例题3】在撑竿跳比赛的横杆下方要放上很厚的海绵垫子.设一位撑竿跳运动员的质量为70 kg,越过横杆后从h=5.6 m高处落下,落在海绵垫上经历时间Δt=1 s停下.求海绵垫对运动员的作用力.(g=10m/s2)
解:下落到静止,以竖直向下为正方向
据动量定理可知:IG+IF=ΔP=0 ---①
自由落体过程:h=gt2/2 ---②
即:mg(t+Δt)+FΔt=0 ---③
代入数据解①②③得:F=-1441N,方向竖直向上
(1)多过程可全程立式求解
(2)动量的变化等于合力的冲量,不是某一个力的冲量
(3)多力共线时,合力冲量时可直接代数运算
【例题4】2020年11月24日,中国用长征五号运载火箭成功发射嫦娥五号探测器,并将其送入预定轨道,运载火箭点火时向下喷气,会对地面产生冲击力。假设火箭喷气口的横截面积为S,喷出气体的速度为v(相对于地面),气体垂直射向地面后竖直速度变为零。已知气体的密度为ρ,重力加速度大小为g,则气体对地面的平均冲击力
解:以气体初速度方向为正方向
据动量定理可知FΔt=ΔP=-Δmv---①
Δt内经过S的气体质量
Δm=ρV=ρvΔtS---②
解①②得F=-ΔP/Δt=-ρSv2
根据牛顿第三定律可知:
气体对地面的冲击力F'=-F=ρSv2
方向竖直向下
v
F
S
动量定理的应用步骤
1、确定研究对象、物理过程,规定正方向
4、根据动量定理列方程,统一单位后代入数据求解。
2、正确受力分析、冲量分析(是否共线),求合外力冲量;
3、初末状态分析,确定初末状态即初末动量;
典型例题
对课后习题进行详细分析,并在此基础之上进行思考和总结。
1、下列说法中正确的是( )
A、冲量是反映力的作用时间积累效果的物理量
B、合力越大,动量变化越大
C、冲量是物体动量变化的原因
D、合力冲量越大,动量变化越大
ACD
课堂练习
2、甲、乙两个质量相同的物体,以相同的初速度分别在粗糙程度不同的水平面上运动,乙物体先停下来,甲物体又经较长时间停下来,下面叙述中正确的是( )
A、甲物体受到的冲量大
B、乙物体受到的冲量大
C、两个物体受到的冲量大小相等
D、无法判断
C
3、某物体做匀变速直线运动,初始动能为E,经过一段时间后速度增加量为2v,动能增加量为3E,则这段时间内物体的动量变化为( )
A. E/2v B. E/v C. 2E/v D. 3E/2v
B
4、 如图所示,用高压水枪喷出的强力水柱冲击右侧的煤层.设水柱直径为 D,水流速度为v,方向水平,水柱垂直于煤层表面,水柱冲击煤层后水的速度为零.手持高压水枪进行操作,进入水枪的水流速度可忽略不计,已知水的密度为 p.下列说法正确的是( )
A. 高压水枪单位时间喷出的水的质量为ρπvD2
B. 高压水枪的功率为ρπD2v3/8
C. 水柱对煤层的平均冲力为ρπD2v2/4·
D. 手对高压水枪的作用力水平向右
BC
5、某游乐园有一喷泉,在水泵作用喷出竖直向上的水柱,将站在冲浪板上的玩偶模型托起,悬停在空中,这一景观可做如下简化,假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出,冲浪板底部为平板且其面积大于水柱的横截面积,保证所有水都能喷到冲浪板的底部。冲击冲浪板后,水在竖直方向的速度立即变为零,已知玩偶模型和冲浪板的总质量为M,水的密度为ρ,重力加速度大小为g,空气阻力及水的粘滞阻力均可忽略不计。
(1)计算玩偶模型在空中悬停时水对冲浪板的冲击力大小
(2)求喷泉单位时间内喷出的水的质量;
(3)求玩偶模型在空中悬停时,冲浪板的底面相对于喷口的高度。
答案 (1)Mg (2)ρv0S
解:(1)模型静止时,据二力平衡可知:F=Mg
(2)Δt内, 喷出水的体积为:ΔV=v0SΔt
质量为:Δm=ρΔV,
单位时间内质量为:m=Δm/Δt=ρv0S
(3)设高度为h,从喷出到板底过程:
据动量定理有:F·Δt=Δp ---②
解①②得:
---①
(忽略水柱微元重力的冲量)
谢谢 再见!
