2022中考数学三轮冲刺考前提分微课01 反比例函数基本图形及其性质探究 课件(共31张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课01 反比例函数基本图形及其性质探究 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览






文档简介
(共31张PPT)
2022年中考数学三轮复习(人教版)
考前提分微课 01
反比例函数基本图形及其性质探究
●基本模型
●性质探究
基本模型
反比例函数y=(k≠0)中k的几何意义
如图W1-1所示,过双曲线上任一点P(x,y)分别作x轴,y轴的垂线,
E,F分别为垂足,则|k|=|xy|=|x|·|y|=PF·PE=S矩形OEPF.
图W1-1
性质探究
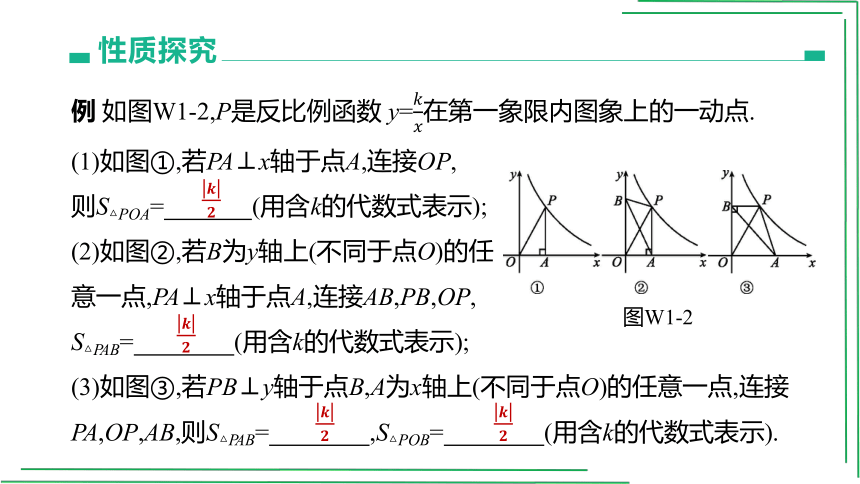
例 如图W1-2,P是反比例函数 y=在第一象限内图象上的一动点.
(1)如图①,若PA⊥x轴于点A,连接OP,
则S△POA= (用含k的代数式表示);
(2)如图②,若B为y轴上(不同于点O)的任
意一点,PA⊥x轴于点A,连接AB,PB,OP,
S△PAB= (用含k的代数式表示);
(3)如图③,若PB⊥y轴于点B,A为x轴上(不同于点O)的任意一点,连接PA,OP,AB,则S△PAB= ,S△POB= (用含k的代数式表示).
图W1-2
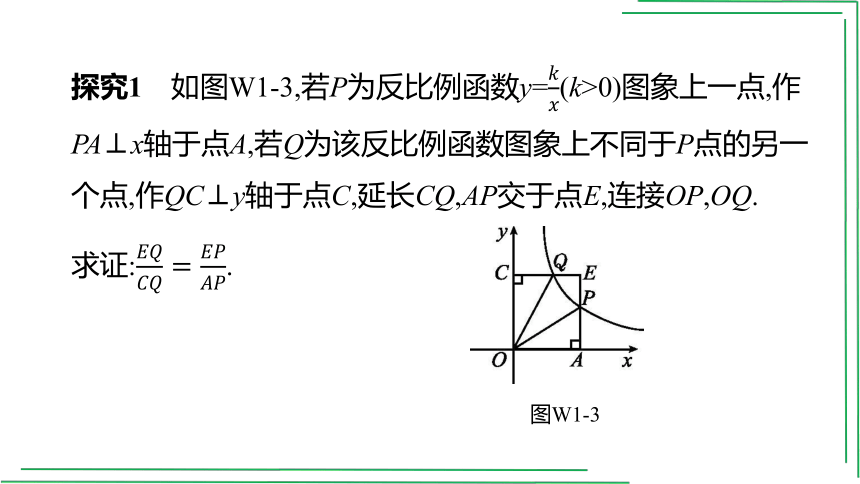
探究1 如图W1-3,若P为反比例函数y=(k>0)图象上一点,作PA⊥x轴于点A,若Q为该反比例函数图象上不同于P点的另一个点,作QC⊥y轴于点C,延长CQ,AP交于点E,连接OP,OQ.
求证:.
图W1-3
证明:由例题的结论可知S△POA=S△QOC=k,
连接OE,易得四边形OAEC为矩形,
∴S△EOA=S△EOC,
∴S△EOP=S△EOA-S△POA=S△EOC-S△QOC=S△EOQ.
又∵,,
∴.
探究2 如图W1-4,在探究1的条件下,连接PQ,AC,请判断PQ与AC有怎样的位置关系,并说明理由.
解:PQ∥AC,理由如下:
由探究1的结论可知,
∴.
又∵∠PEQ=∠AEC,∴△PEQ∽△AEC,
∴∠EQP=∠ECA,∴PQ∥AC.
图W1-4
探究3 如图W1-5,在探究2的条件下,双向延长PQ,分别交x轴和y轴于点M,N,请判断线段PM与QN的数量关系,并说明理由.
解:PM=QN.理由如下:
∵CE∥OA,AC∥PQ,
∴四边形AMQC为平行四边形,∴AC=QM.
同理,四边形APNC为平行四边形,
∴AC=PN,∴QM=PN,
∴QM-PQ=PN-PQ,即PM=QN.
图W1-5
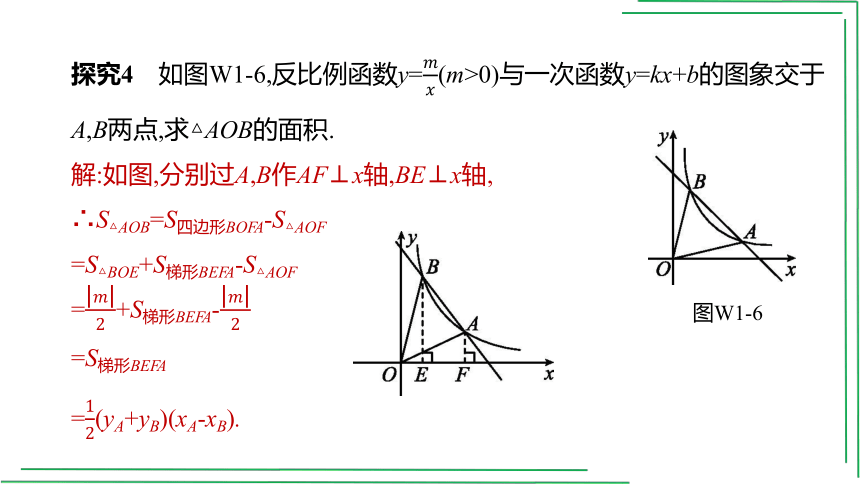
探究4 如图W1-6,反比例函数y=(m>0)与一次函数y=kx+b的图象交于A,B两点,求△AOB的面积.
解:如图,分别过A,B作AF⊥x轴,BE⊥x轴,
∴S△AOB=S四边形BOFA-S△AOF
=S△BOE+S梯形BEFA-S△AOF
=+S梯形BEFA-
=S梯形BEFA
=(yA+yB)(xA-xB).
图W1-6
模型应用
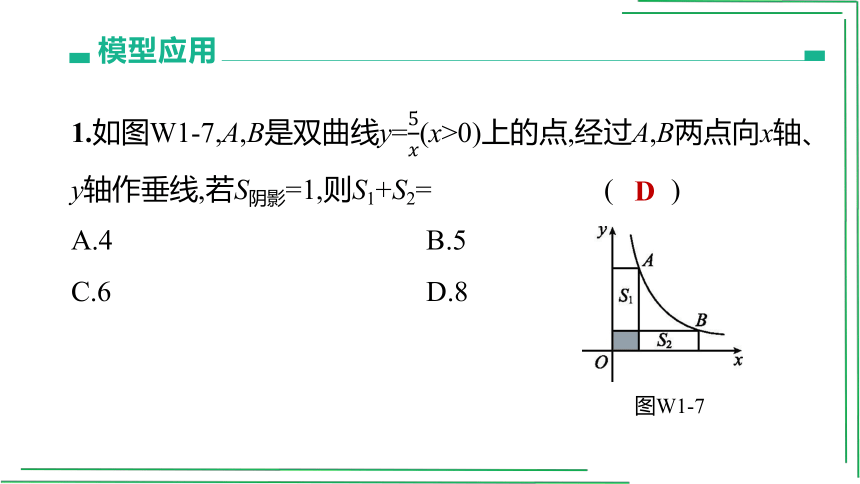
1.如图W1-7,A,B是双曲线y=(x>0)上的点,经过A,B两点向x轴、y轴作垂线,若S阴影=1,则S1+S2= ( )
A.4 B.5
C.6 D.8
图W1-7
D
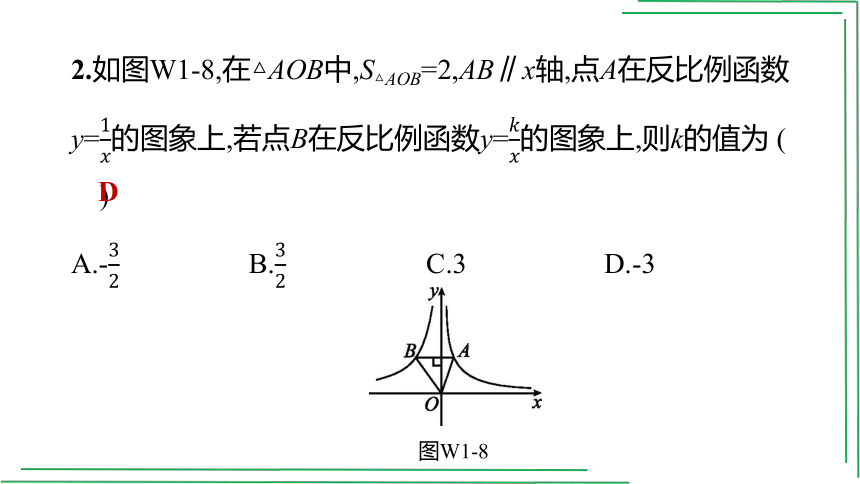
2.如图W1-8,在△AOB中,S△AOB=2,AB∥x轴,点A在反比例函数y=的图象上,若点B在反比例函数y=的图象上,则k的值为 ( )
A.- B. C.3 D.-3
图W1-8
D
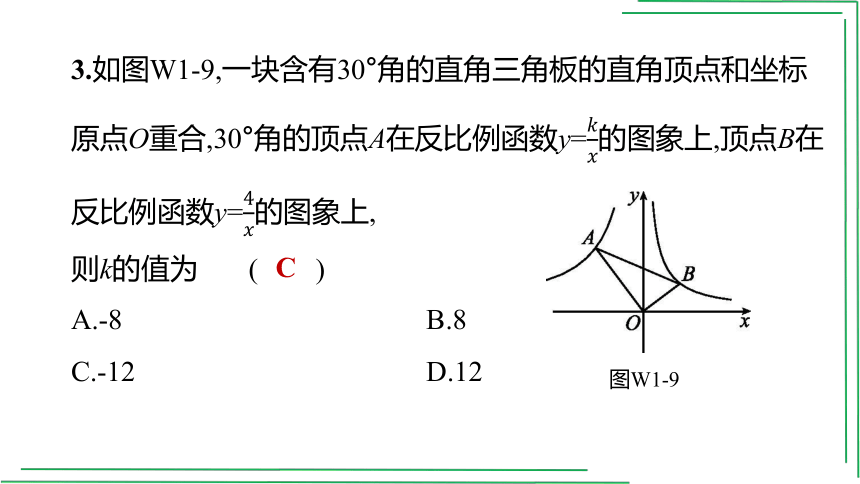
3.如图W1-9,一块含有30°角的直角三角板的直角顶点和坐标原点O重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,
则k的值为 ( )
A.-8 B.8
C.-12 D.12
图W1-9
C
[解析]过点A,B分别作x轴的垂线,垂足分别为C,D,
在Rt△ABO中,
∠BAO=30°,∠AOB=90°,∴=tan30°=,
∵∠BOD+∠OBD=90°,∠BOD+∠AOC=180°-90°=90°,
∴∠OBD=∠AOC,
又∵∠ACO=∠ODB=90°,
∴△AOC∽△OBD,∴=()2=,
又∵点B在y=的图象上,
∴S△OBD=×4=2,
∴S△AOC=3S△OBD=3×2=6=|k|,
∴k=±12,
又∵点A在第二象限,
∴k=-12,
故选C.
4.[2021·扬州]如图W1-10,点P是函数y=(k1>0,x>0)的图象上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A,B,交函数y=(k2>0,x>0)的图象于点C,D,连接OC,OD,CD,AB,其中k1>k2.下列结论:①CD∥AB;②S△OCD=;③S△DCP=,
其中正确的是 ( )
A.①② B.①③
C.②③ D.①
图W1-10
B
[解析] ∵PB⊥y轴,PA⊥x轴,点P在函数y=的图象上,点C,D在函数y=的图象上,
设P(m,),则C(m,),A(m,0),B(0,),∴PC=,
令,得x=,即D(,),∴PD=m-,
∴,,即.
又∠DPC=∠BPA,∴△PDC∽△PBA,∴∠PDC=∠PBA,
∴CD∥AB,故①正确;
△PDC的面积=×PD×PC=,故③正确;
S△OCD=S四边形OAPB-S△OCA-S△OBD-S△DPC=k1-k2-k2-,故②错误.
5.如图W1-11,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点.若E是AB的中点,S△BEF=2,则k的值为 .
图W1-11
8
[解析]连接OF,因为E为AB的中点,所以F为BC的中点,即BF=CF.所以S△COF=2S△BFE=4,所以k=8.
6.[2019·沈阳]如图W1-12,正比例函数y1=k1x的图象与反比例函数y2=(x>0)的图象相交于点A(,2),B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是
.
图W1-12
2
[解析]易得B(3,2),
又∵A(,2),
∴S△AOB==2.
7.[2019·本溪]如图W1-13,在平面直角坐标系中,等边三角形OAB和菱形OCDE的边OA,OE都在x轴上,点C在OB边上,S△ABD
=,反比例函数y=(x>0)的图象经过点B,则k的值为 .
图W1-13
[解析]连接OD,
∵△OAB是等边三角形,
∴∠AOB=∠OAB=60°,∴∠EOB=120°.
∵四边形OCDE是菱形,
∴∠EOD=∠EOB=60°=∠OAB,
∴OD∥AB,∴S△AOB=S△ABD=,∴k=.
8.如图W1-14,已知直线y=-x+2分别与x轴,y轴交于A,B两点,与双曲线y=交于E,F两点.若AB=2EF,则k的值是 .
图W1-14
[解析]作FG⊥y轴于点G.
由基本图形结论可知AE=BF,
又∵AB=2EF,
∴BF∶EF∶AE=1∶2∶1,
∴,
易得AO=BO=2,∴FG=BG=,OG=,
∴F(,),∴k=.
G
9.[2019·衢州]如图W1-15,在平面直角坐标系中,O为坐标原点, ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=(k≠0)的图象经过点C,且S△BEF=1,则k的值为 .
图W1-15
24
[解析]连接OC,BD,
∵将△AOD沿y轴翻折,使点A落在x轴上的点E处,
∴OA=OE,
∵点B恰好为OE的中点,
∴OE=2OB,∴OA=2OB,
设OB=BE=x,则OA=2x,∴AB=3x,
∵四边形ABCD是平行四边形,
∴CD=AB=3x,
∵CD∥AB,∴△CDF∽△BEF,
∴,
∵S△BEF=1,
∴S△BDF=3,S△CDF=9,
∴S△BCD=12,
∴S△CDO=S△BDC=12,
∴k=2S△CDO=24.
10.如图W1-16,在△AOB中,OC平分∠AOB,,反比例函数y=(k<0)的图象经过A,C两点,点B在x轴上,若△AOB的面积为7,则k的值为 .
图W1-16
-
[解析]∵OC平分∠AOB,,
∴,
延长BA交y轴于点E,作AF⊥OB于F,
易得AE∶AC∶BC=3∶4∶3,
∴,∴,
∵S△AOB=7,∴S△AOF=,∴k=-.
11.如图W1-17,点E,F在函数y=(x>0)的图象上,直线EF分别与x轴,y轴交于点A,B,且BE∶BF=1∶m.过点E作EP⊥y轴于点P,已知△OEP的面积为1.则k的值是 ,
△OEF的面积是 (用含m的式子表示).
图W1-17
2
m-
[解析]由基本图形结论可知,k=2S△POE=2.作FG⊥OP于G,易得△BPE∽△BGF,所以.
设E(a,),则F(am,),
由基本图形结论可知,
S△OEF=(·am-a·)=m-.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
考前提分微课 01
反比例函数基本图形及其性质探究
●基本模型
●性质探究
基本模型
反比例函数y=(k≠0)中k的几何意义
如图W1-1所示,过双曲线上任一点P(x,y)分别作x轴,y轴的垂线,
E,F分别为垂足,则|k|=|xy|=|x|·|y|=PF·PE=S矩形OEPF.
图W1-1
性质探究
例 如图W1-2,P是反比例函数 y=在第一象限内图象上的一动点.
(1)如图①,若PA⊥x轴于点A,连接OP,
则S△POA= (用含k的代数式表示);
(2)如图②,若B为y轴上(不同于点O)的任
意一点,PA⊥x轴于点A,连接AB,PB,OP,
S△PAB= (用含k的代数式表示);
(3)如图③,若PB⊥y轴于点B,A为x轴上(不同于点O)的任意一点,连接PA,OP,AB,则S△PAB= ,S△POB= (用含k的代数式表示).
图W1-2
探究1 如图W1-3,若P为反比例函数y=(k>0)图象上一点,作PA⊥x轴于点A,若Q为该反比例函数图象上不同于P点的另一个点,作QC⊥y轴于点C,延长CQ,AP交于点E,连接OP,OQ.
求证:.
图W1-3
证明:由例题的结论可知S△POA=S△QOC=k,
连接OE,易得四边形OAEC为矩形,
∴S△EOA=S△EOC,
∴S△EOP=S△EOA-S△POA=S△EOC-S△QOC=S△EOQ.
又∵,,
∴.
探究2 如图W1-4,在探究1的条件下,连接PQ,AC,请判断PQ与AC有怎样的位置关系,并说明理由.
解:PQ∥AC,理由如下:
由探究1的结论可知,
∴.
又∵∠PEQ=∠AEC,∴△PEQ∽△AEC,
∴∠EQP=∠ECA,∴PQ∥AC.
图W1-4
探究3 如图W1-5,在探究2的条件下,双向延长PQ,分别交x轴和y轴于点M,N,请判断线段PM与QN的数量关系,并说明理由.
解:PM=QN.理由如下:
∵CE∥OA,AC∥PQ,
∴四边形AMQC为平行四边形,∴AC=QM.
同理,四边形APNC为平行四边形,
∴AC=PN,∴QM=PN,
∴QM-PQ=PN-PQ,即PM=QN.
图W1-5
探究4 如图W1-6,反比例函数y=(m>0)与一次函数y=kx+b的图象交于A,B两点,求△AOB的面积.
解:如图,分别过A,B作AF⊥x轴,BE⊥x轴,
∴S△AOB=S四边形BOFA-S△AOF
=S△BOE+S梯形BEFA-S△AOF
=+S梯形BEFA-
=S梯形BEFA
=(yA+yB)(xA-xB).
图W1-6
模型应用
1.如图W1-7,A,B是双曲线y=(x>0)上的点,经过A,B两点向x轴、y轴作垂线,若S阴影=1,则S1+S2= ( )
A.4 B.5
C.6 D.8
图W1-7
D
2.如图W1-8,在△AOB中,S△AOB=2,AB∥x轴,点A在反比例函数y=的图象上,若点B在反比例函数y=的图象上,则k的值为 ( )
A.- B. C.3 D.-3
图W1-8
D
3.如图W1-9,一块含有30°角的直角三角板的直角顶点和坐标原点O重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,
则k的值为 ( )
A.-8 B.8
C.-12 D.12
图W1-9
C
[解析]过点A,B分别作x轴的垂线,垂足分别为C,D,
在Rt△ABO中,
∠BAO=30°,∠AOB=90°,∴=tan30°=,
∵∠BOD+∠OBD=90°,∠BOD+∠AOC=180°-90°=90°,
∴∠OBD=∠AOC,
又∵∠ACO=∠ODB=90°,
∴△AOC∽△OBD,∴=()2=,
又∵点B在y=的图象上,
∴S△OBD=×4=2,
∴S△AOC=3S△OBD=3×2=6=|k|,
∴k=±12,
又∵点A在第二象限,
∴k=-12,
故选C.
4.[2021·扬州]如图W1-10,点P是函数y=(k1>0,x>0)的图象上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A,B,交函数y=(k2>0,x>0)的图象于点C,D,连接OC,OD,CD,AB,其中k1>k2.下列结论:①CD∥AB;②S△OCD=;③S△DCP=,
其中正确的是 ( )
A.①② B.①③
C.②③ D.①
图W1-10
B
[解析] ∵PB⊥y轴,PA⊥x轴,点P在函数y=的图象上,点C,D在函数y=的图象上,
设P(m,),则C(m,),A(m,0),B(0,),∴PC=,
令,得x=,即D(,),∴PD=m-,
∴,,即.
又∠DPC=∠BPA,∴△PDC∽△PBA,∴∠PDC=∠PBA,
∴CD∥AB,故①正确;
△PDC的面积=×PD×PC=,故③正确;
S△OCD=S四边形OAPB-S△OCA-S△OBD-S△DPC=k1-k2-k2-,故②错误.
5.如图W1-11,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点.若E是AB的中点,S△BEF=2,则k的值为 .
图W1-11
8
[解析]连接OF,因为E为AB的中点,所以F为BC的中点,即BF=CF.所以S△COF=2S△BFE=4,所以k=8.
6.[2019·沈阳]如图W1-12,正比例函数y1=k1x的图象与反比例函数y2=(x>0)的图象相交于点A(,2),B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是
.
图W1-12
2
[解析]易得B(3,2),
又∵A(,2),
∴S△AOB==2.
7.[2019·本溪]如图W1-13,在平面直角坐标系中,等边三角形OAB和菱形OCDE的边OA,OE都在x轴上,点C在OB边上,S△ABD
=,反比例函数y=(x>0)的图象经过点B,则k的值为 .
图W1-13
[解析]连接OD,
∵△OAB是等边三角形,
∴∠AOB=∠OAB=60°,∴∠EOB=120°.
∵四边形OCDE是菱形,
∴∠EOD=∠EOB=60°=∠OAB,
∴OD∥AB,∴S△AOB=S△ABD=,∴k=.
8.如图W1-14,已知直线y=-x+2分别与x轴,y轴交于A,B两点,与双曲线y=交于E,F两点.若AB=2EF,则k的值是 .
图W1-14
[解析]作FG⊥y轴于点G.
由基本图形结论可知AE=BF,
又∵AB=2EF,
∴BF∶EF∶AE=1∶2∶1,
∴,
易得AO=BO=2,∴FG=BG=,OG=,
∴F(,),∴k=.
G
9.[2019·衢州]如图W1-15,在平面直角坐标系中,O为坐标原点, ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=(k≠0)的图象经过点C,且S△BEF=1,则k的值为 .
图W1-15
24
[解析]连接OC,BD,
∵将△AOD沿y轴翻折,使点A落在x轴上的点E处,
∴OA=OE,
∵点B恰好为OE的中点,
∴OE=2OB,∴OA=2OB,
设OB=BE=x,则OA=2x,∴AB=3x,
∵四边形ABCD是平行四边形,
∴CD=AB=3x,
∵CD∥AB,∴△CDF∽△BEF,
∴,
∵S△BEF=1,
∴S△BDF=3,S△CDF=9,
∴S△BCD=12,
∴S△CDO=S△BDC=12,
∴k=2S△CDO=24.
10.如图W1-16,在△AOB中,OC平分∠AOB,,反比例函数y=(k<0)的图象经过A,C两点,点B在x轴上,若△AOB的面积为7,则k的值为 .
图W1-16
-
[解析]∵OC平分∠AOB,,
∴,
延长BA交y轴于点E,作AF⊥OB于F,
易得AE∶AC∶BC=3∶4∶3,
∴,∴,
∵S△AOB=7,∴S△AOF=,∴k=-.
11.如图W1-17,点E,F在函数y=(x>0)的图象上,直线EF分别与x轴,y轴交于点A,B,且BE∶BF=1∶m.过点E作EP⊥y轴于点P,已知△OEP的面积为1.则k的值是 ,
△OEF的面积是 (用含m的式子表示).
图W1-17
2
m-
[解析]由基本图形结论可知,k=2S△POE=2.作FG⊥OP于G,易得△BPE∽△BGF,所以.
设E(a,),则F(am,),
由基本图形结论可知,
S△OEF=(·am-a·)=m-.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
