2022中考数学三轮冲刺考前提分微课02 坐标系中的三角形面积问题 课件(共28张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课02 坐标系中的三角形面积问题 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:14:18 | ||
图片预览







文档简介
(共28张PPT)
2022年中考数学三轮复习(人教版)
提分微课 02
坐标系中的三角形面积问题
平面直角坐标系中的面积问题,一般涉及求面积、求面积的最大值,或解决面积之间的关系等,解题策略主要有三种:①公式法;②割补法;③等积转化法.
公式法求图形的面积
类型一
公式法求三角形的面积适用于一边在坐标轴上(或平行于坐标轴)的三角形的面积计算.
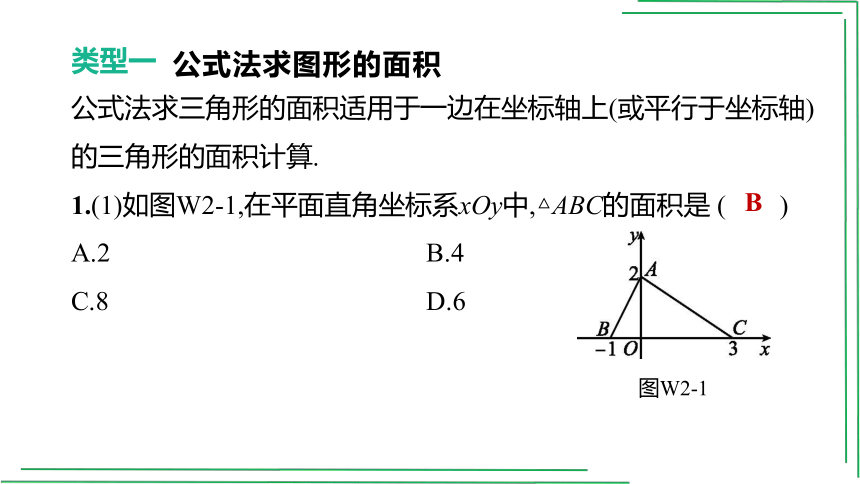
1.(1)如图W2-1,在平面直角坐标系xOy中,△ABC的面积是 ( )
A.2 B.4
C.8 D.6
图W2-1
B
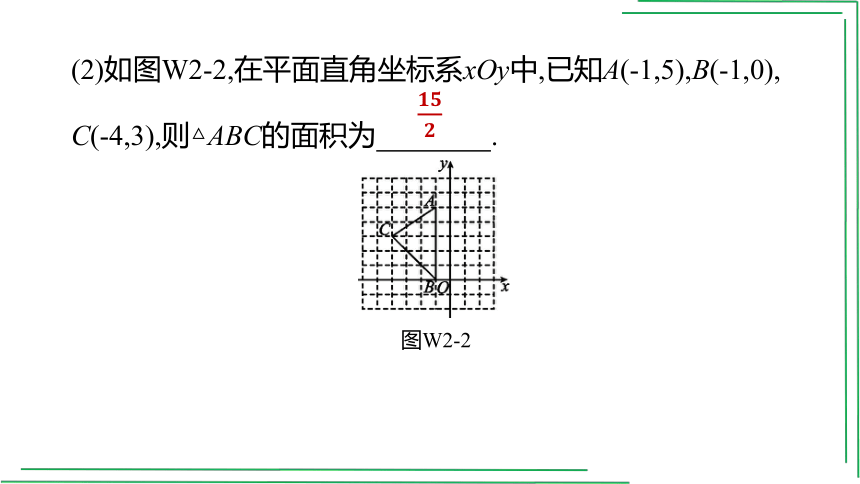
(2)如图W2-2,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),
C(-4,3),则△ABC的面积为 .
图W2-2
2.已知点A,B,C的坐标,分别求△ABC的面积.
(1)A(-1,0),B(3,0),C(4,-3),S△ABC= ;
(2)A(2,0),B(0,1),C(0,4),S△ABC= .
3.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为 ( )
A.(-4,0) B.(6,0)
C.(-4,0)或(6,0) D.无法确定
6
3
C
4.如图W2-3,已知抛物线y=-x2+bx+c经过点A(2,0),B(0,-6)两点,该抛物线的对称轴与x轴交于点C,连接BA,BC.
(1)求这个抛物线的解析式.
(2)求△ABC的面积.
(3)在抛物线上是否存在点D(x,y),
使S△ACD=S△ABC 若存在,求出点D
的坐标;若不存在,说明理由.
图W2-3
(1)求这个抛物线的解析式.
解:(1)将点A(2,0),B(0,-6)的坐标
代入y=-x2+bx+c,得
解得
∴抛物线的解析式为y=-x2+4x-6.
图W2-3
(2)求△ABC的面积.
(2)∵y=-x2+4x-6=-(x-4)2+2,
∴点C坐标为(4,0),
则△ABC的面积为×(4-2)×6=6.
图W2-3
(3)在抛物线上是否存在点D(x,y),使S△ACD=S△ABC 若存在,求出点D
的坐标;若不存在,说明理由.
图W2-3
(3)存在,由S△ACD=S△ABC可得·|y|·2=3,
则|y|=3,即y=3或y=-3,
∵当x=4时,y的最大值为2<3,∴y=3舍去;
当y=-3时,-(x-4)2+2=-3,解得x=4±,
则点D的坐标为(4-,-3)或(4+,-3).
[通性通法]
三角形的一边在坐标轴上
三角形的一边与坐标轴平行
直接使用三角形的面积公式S=AB·h,其中AB为三角形在坐标轴上(或平行于坐标轴)的一边,h为AB边上的高.
割补法求图形的面积
类型二
割补法适用于三边都不在坐标轴上(或都不平行于坐标轴)的三角形的面积计算.
5.如图W2-4,在△AOB中,A,B两点的坐标分别为(2,4)和(6,2),则△AOB的面积为 .
图W2-4
10
[解析]如图,过A作x轴的平行线l交y轴于点E,过B作x轴的垂线,交直线l于点C,交x轴于点D,则
S矩形ECDO=6×4=24,SRt△AEO=×4×2=4,
SRt△ABC=×2×4=4,SRt△OBD=×6×2=6,
∴S△OAB=S矩形ECDO-SRt△ABC-SRt△AEO-SRt△OBD=10.
∴△AOB的面积是10.
6.如图W2-5,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
(1)△ABC的面积为 ;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,则点P的坐标为 .
图W2-5
4
(10,0)或(-6,0)
[解析](1)过点C作CD⊥x轴,CE⊥y轴,垂足分别为D,E.
S△ABC=S四边形CDOE-S△AEC-S△ABO-S△BCD=
3×4-×2×4-×1×2-×2×3=12-4-1-3=4.
(2)设点P的坐标为(x,0),则BP=|x-2|.
∵△ABP与△ABC的面积相等,∴×1×|x-2|=4,解得x=10或x=-6,
∴点P的坐标为(10,0)或(-6,0).
7.如图W2-6,已知抛物线的解析式为y=-x2+2x+3,与坐标轴分别交于A,B两点,点P为直线AB上方的抛物线上一动点,则当点P的坐标为多少时,△PAB的面积最大,并求出这个最大面积.
解法一:割补法
直角坐标系下的“斜”三角形的面积求
法均可以通过切割形式转化为“正”三
角形来解决,常用竖切法.
图W2-6
如图,过点P作PC⊥x轴交直线AB于点C,交x轴于点D,则△PAB被线段PC分割成了两个三角形,
过点B作BE⊥PC于E,
则S△PAB=S△PBC+S△PAC
=PC×BE+PC×AD=PC×(BE+AD)=PC×AO.
∵AO为定值,∴当PC长度最大时,△PAB的面积最大.
可求直线AB的解析式为y=-x+3,设点P的坐标为(m,-m2+2m+3),则点C的坐标为(m,-m+3),
∵点P始终在点C上方,∴PC=-m2+2m+3-(-m+3)=-m2+3m,
∴S△PAB=PC×AO=×(-m2+3m)×3=-m2+m=-,
∵点P在直线AB上方的抛物线上运动,
∴点P横坐标m的取值范围为0∴当点P的横坐标为时,△PAB的面积
最大值为,此时点P的坐标为(,).
解法二:等积法
如图,连接OP,过点P作x轴,y轴的垂线,垂足分别为N,M,设点P的坐标为(m,-m2+2m+3),
则S△PAB=S△PBO+S△PAO-S△ABO
=OB×PM+OA×PN-OA×OB
=×3×m+×3×(-m2+2m+3)-×3×3
=-m2+m=-,下同解法一.
解法三:等积转化法
分析可知:当点P到AB的距离最大时,△PAB的面积最大.
根据“平行线间的距离处处相等”可知,平移直线AB,当直线AB与抛物线只有一个公共点时,面积达到最大值,此时的公共点即为点P.
由抛物线的解析式y=-x2+2x+3可知点A,B的坐标分别为A(3,0),B(0,3),
易得直线AB的解析式为y=-x+3.
如图,设过点P且平行于直线AB的直线PC的解析式为
y=-x+b,∴整理得:x2-3x+b-3=0.
∵直线与抛物线只有一个交点即一元二次方程有两个相等的实数根,
∴Δ=0,即(-3)2-4(b-3)=0,解得b=,即直线PC的解析式为y=-x+,
与抛物线联立可解得点P的坐标为(,),
∴S△PAB=S△CAB=CB·OA=×3=,
即点P的坐标为(,)时,△PAB面积的最大值为.
[通性通法]
不规则图形或不好直接计算面积的图形,一般可采取“割补法”,转化为规则图形或可直接计算图形面积的“加加减减”.
(1)分割法
S△ABC=S△ABD+S△BCD
S△ABC=S△ABD+S△ACD
(2)补形法
S△ABC=S矩形CFEG-S△ABE-S△BCF-S△ACG
等积转化求图形的面积
类型三
适用于图中有平行条件或易于转化面积的面积计算.
8.如图W2-7,在平面直角坐标系中,直线y=2x与函数y=(x>0)的图象交于点A(m,2),将直线y=2x平移,与函数
y=(x>0)的图象交于点P,且△POA的面积为2.
(1)求k的值;
(2)求平移后的直线的解析式.
图W2-7
(1)求k的值;
解:(1)∵点A(m,2)在直线y=2x上,
∴2=2m,∴m=1.
∵点A(1,2)在函数y=的图象上,∴k=2.
图W2-7
(2)求平移后的直线的解析式.
(2)若直线y=2x向下平移,
如图,设平移后的直线与y轴交于点B,
连接AB,则S△POA=S△AOB=2.
过点A作y轴的垂线AC,垂足为点C,
则AC=1.∴OB·AC=2.∴OB=4.
∴向下平移后的直线解析式为y=2x-4.
同理,若直线y=2x向上平移,则平移后的直线解析式为y=2x+4.
综上,平移后的直线的解析式为y=2x+4或y=2x-4.
图W2-7
[通性通法]
在平面直角坐标系中,常利用平行线间的距离处处相等,根据同底等高的三角形面积相等,作已知三角形一边的平行线来进行等积变换.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
提分微课 02
坐标系中的三角形面积问题
平面直角坐标系中的面积问题,一般涉及求面积、求面积的最大值,或解决面积之间的关系等,解题策略主要有三种:①公式法;②割补法;③等积转化法.
公式法求图形的面积
类型一
公式法求三角形的面积适用于一边在坐标轴上(或平行于坐标轴)的三角形的面积计算.
1.(1)如图W2-1,在平面直角坐标系xOy中,△ABC的面积是 ( )
A.2 B.4
C.8 D.6
图W2-1
B
(2)如图W2-2,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),
C(-4,3),则△ABC的面积为 .
图W2-2
2.已知点A,B,C的坐标,分别求△ABC的面积.
(1)A(-1,0),B(3,0),C(4,-3),S△ABC= ;
(2)A(2,0),B(0,1),C(0,4),S△ABC= .
3.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标为 ( )
A.(-4,0) B.(6,0)
C.(-4,0)或(6,0) D.无法确定
6
3
C
4.如图W2-3,已知抛物线y=-x2+bx+c经过点A(2,0),B(0,-6)两点,该抛物线的对称轴与x轴交于点C,连接BA,BC.
(1)求这个抛物线的解析式.
(2)求△ABC的面积.
(3)在抛物线上是否存在点D(x,y),
使S△ACD=S△ABC 若存在,求出点D
的坐标;若不存在,说明理由.
图W2-3
(1)求这个抛物线的解析式.
解:(1)将点A(2,0),B(0,-6)的坐标
代入y=-x2+bx+c,得
解得
∴抛物线的解析式为y=-x2+4x-6.
图W2-3
(2)求△ABC的面积.
(2)∵y=-x2+4x-6=-(x-4)2+2,
∴点C坐标为(4,0),
则△ABC的面积为×(4-2)×6=6.
图W2-3
(3)在抛物线上是否存在点D(x,y),使S△ACD=S△ABC 若存在,求出点D
的坐标;若不存在,说明理由.
图W2-3
(3)存在,由S△ACD=S△ABC可得·|y|·2=3,
则|y|=3,即y=3或y=-3,
∵当x=4时,y的最大值为2<3,∴y=3舍去;
当y=-3时,-(x-4)2+2=-3,解得x=4±,
则点D的坐标为(4-,-3)或(4+,-3).
[通性通法]
三角形的一边在坐标轴上
三角形的一边与坐标轴平行
直接使用三角形的面积公式S=AB·h,其中AB为三角形在坐标轴上(或平行于坐标轴)的一边,h为AB边上的高.
割补法求图形的面积
类型二
割补法适用于三边都不在坐标轴上(或都不平行于坐标轴)的三角形的面积计算.
5.如图W2-4,在△AOB中,A,B两点的坐标分别为(2,4)和(6,2),则△AOB的面积为 .
图W2-4
10
[解析]如图,过A作x轴的平行线l交y轴于点E,过B作x轴的垂线,交直线l于点C,交x轴于点D,则
S矩形ECDO=6×4=24,SRt△AEO=×4×2=4,
SRt△ABC=×2×4=4,SRt△OBD=×6×2=6,
∴S△OAB=S矩形ECDO-SRt△ABC-SRt△AEO-SRt△OBD=10.
∴△AOB的面积是10.
6.如图W2-5,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
(1)△ABC的面积为 ;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,则点P的坐标为 .
图W2-5
4
(10,0)或(-6,0)
[解析](1)过点C作CD⊥x轴,CE⊥y轴,垂足分别为D,E.
S△ABC=S四边形CDOE-S△AEC-S△ABO-S△BCD=
3×4-×2×4-×1×2-×2×3=12-4-1-3=4.
(2)设点P的坐标为(x,0),则BP=|x-2|.
∵△ABP与△ABC的面积相等,∴×1×|x-2|=4,解得x=10或x=-6,
∴点P的坐标为(10,0)或(-6,0).
7.如图W2-6,已知抛物线的解析式为y=-x2+2x+3,与坐标轴分别交于A,B两点,点P为直线AB上方的抛物线上一动点,则当点P的坐标为多少时,△PAB的面积最大,并求出这个最大面积.
解法一:割补法
直角坐标系下的“斜”三角形的面积求
法均可以通过切割形式转化为“正”三
角形来解决,常用竖切法.
图W2-6
如图,过点P作PC⊥x轴交直线AB于点C,交x轴于点D,则△PAB被线段PC分割成了两个三角形,
过点B作BE⊥PC于E,
则S△PAB=S△PBC+S△PAC
=PC×BE+PC×AD=PC×(BE+AD)=PC×AO.
∵AO为定值,∴当PC长度最大时,△PAB的面积最大.
可求直线AB的解析式为y=-x+3,设点P的坐标为(m,-m2+2m+3),则点C的坐标为(m,-m+3),
∵点P始终在点C上方,∴PC=-m2+2m+3-(-m+3)=-m2+3m,
∴S△PAB=PC×AO=×(-m2+3m)×3=-m2+m=-,
∵点P在直线AB上方的抛物线上运动,
∴点P横坐标m的取值范围为0
最大值为,此时点P的坐标为(,).
解法二:等积法
如图,连接OP,过点P作x轴,y轴的垂线,垂足分别为N,M,设点P的坐标为(m,-m2+2m+3),
则S△PAB=S△PBO+S△PAO-S△ABO
=OB×PM+OA×PN-OA×OB
=×3×m+×3×(-m2+2m+3)-×3×3
=-m2+m=-,下同解法一.
解法三:等积转化法
分析可知:当点P到AB的距离最大时,△PAB的面积最大.
根据“平行线间的距离处处相等”可知,平移直线AB,当直线AB与抛物线只有一个公共点时,面积达到最大值,此时的公共点即为点P.
由抛物线的解析式y=-x2+2x+3可知点A,B的坐标分别为A(3,0),B(0,3),
易得直线AB的解析式为y=-x+3.
如图,设过点P且平行于直线AB的直线PC的解析式为
y=-x+b,∴整理得:x2-3x+b-3=0.
∵直线与抛物线只有一个交点即一元二次方程有两个相等的实数根,
∴Δ=0,即(-3)2-4(b-3)=0,解得b=,即直线PC的解析式为y=-x+,
与抛物线联立可解得点P的坐标为(,),
∴S△PAB=S△CAB=CB·OA=×3=,
即点P的坐标为(,)时,△PAB面积的最大值为.
[通性通法]
不规则图形或不好直接计算面积的图形,一般可采取“割补法”,转化为规则图形或可直接计算图形面积的“加加减减”.
(1)分割法
S△ABC=S△ABD+S△BCD
S△ABC=S△ABD+S△ACD
(2)补形法
S△ABC=S矩形CFEG-S△ABE-S△BCF-S△ACG
等积转化求图形的面积
类型三
适用于图中有平行条件或易于转化面积的面积计算.
8.如图W2-7,在平面直角坐标系中,直线y=2x与函数y=(x>0)的图象交于点A(m,2),将直线y=2x平移,与函数
y=(x>0)的图象交于点P,且△POA的面积为2.
(1)求k的值;
(2)求平移后的直线的解析式.
图W2-7
(1)求k的值;
解:(1)∵点A(m,2)在直线y=2x上,
∴2=2m,∴m=1.
∵点A(1,2)在函数y=的图象上,∴k=2.
图W2-7
(2)求平移后的直线的解析式.
(2)若直线y=2x向下平移,
如图,设平移后的直线与y轴交于点B,
连接AB,则S△POA=S△AOB=2.
过点A作y轴的垂线AC,垂足为点C,
则AC=1.∴OB·AC=2.∴OB=4.
∴向下平移后的直线解析式为y=2x-4.
同理,若直线y=2x向上平移,则平移后的直线解析式为y=2x+4.
综上,平移后的直线的解析式为y=2x+4或y=2x-4.
图W2-7
[通性通法]
在平面直角坐标系中,常利用平行线间的距离处处相等,根据同底等高的三角形面积相等,作已知三角形一边的平行线来进行等积变换.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
