2022中考数学三轮冲刺考前提分微课04 关于中点的联想 课件(共51张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课04 关于中点的联想 课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:12:09 | ||
图片预览






文档简介
(共51张PPT)
2022年中考数学三轮复习(人教版)
提分微课 04
关于中点的联想
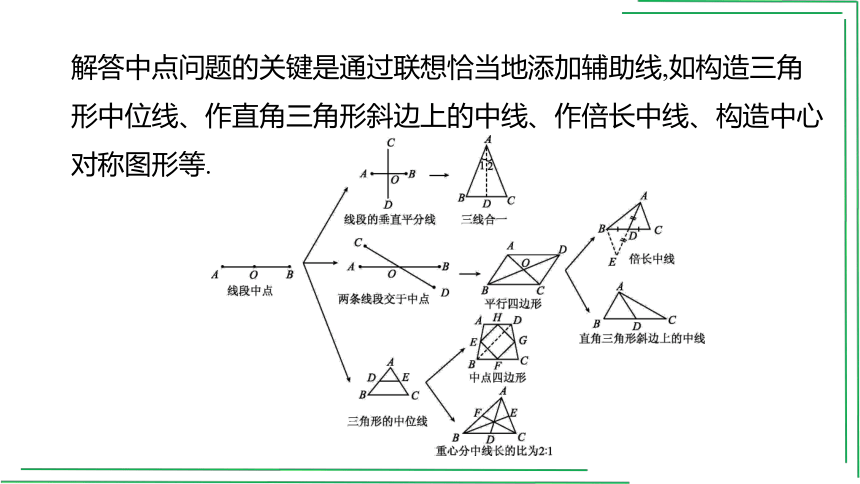
解答中点问题的关键是通过联想恰当地添加辅助线,如构造三角形中位线、作直角三角形斜边上的中线、作倍长中线、构造中心对称图形等.
类型一
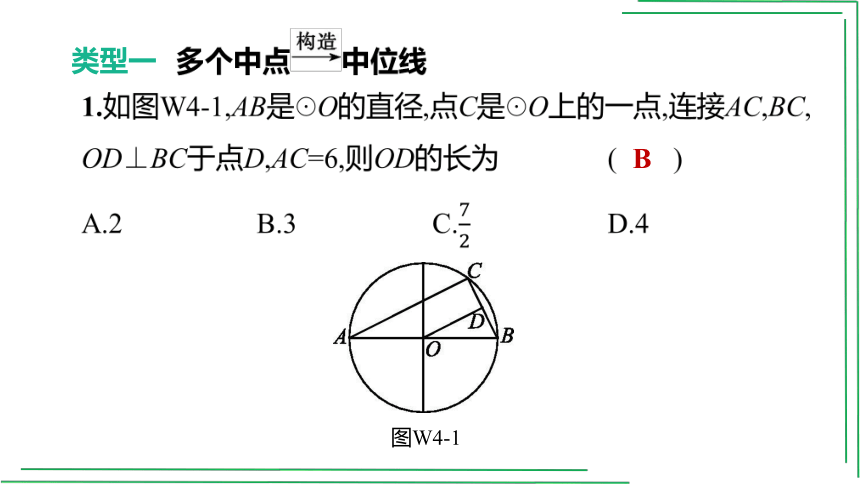
1.如图W4-1,AB是☉O的直径,点C是☉O上的一点,连接AC,BC,
OD⊥BC于点D,AC=6,则OD的长为 ( )
A.2 B.3 C. D.4
图W4-1
B
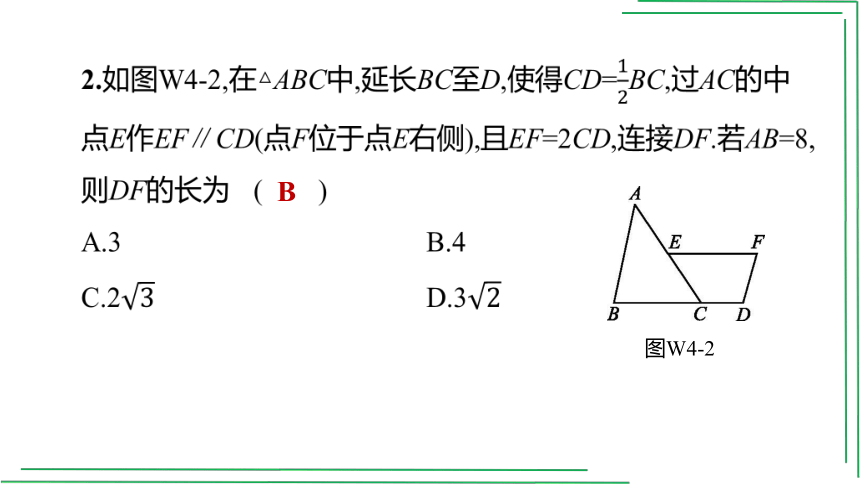
2.如图W4-2,在△ABC中,延长BC至D,使得CD=BC,过AC的中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为 ( )
A.3 B.4
C.2 D.3
图W4-2
B
[解析]如图,取BC的中点G,连接EG,
∵E是AC的中点,∴EG是△ABC的中位线,
∴EG=AB=×8=4,
设CD=x,则EF=BC=2x,
∴BG=CG=x,∴EF=2x=DG,
∵EF∥CD,∴四边形EGDF是平行四边形,
∴DF=EG=4,故选B.
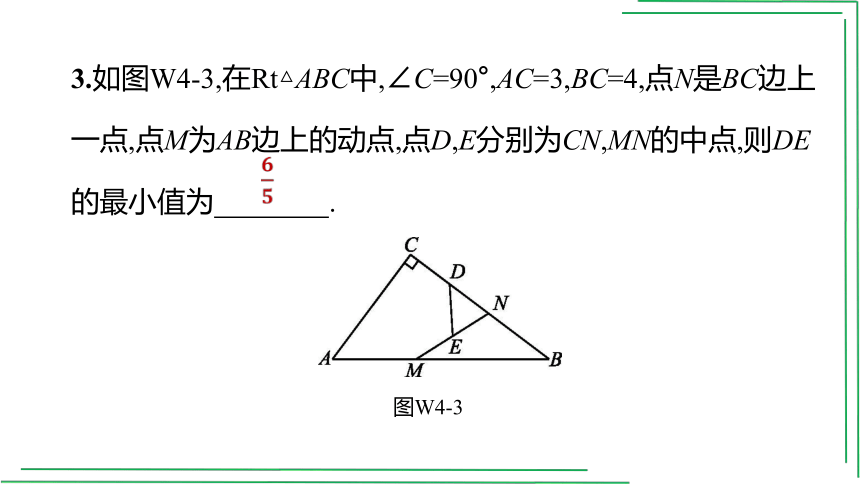
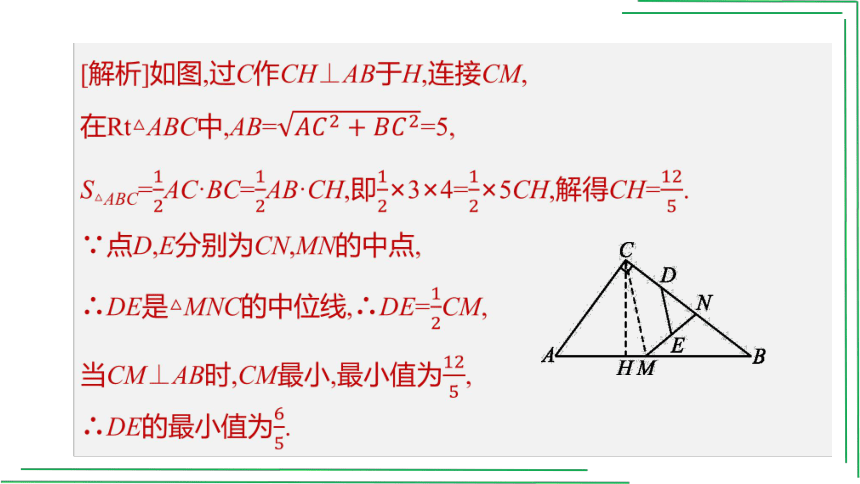
3.如图W4-3,在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D,E分别为CN,MN的中点,则DE
的最小值为 .
图W4-3
[解析]如图,过C作CH⊥AB于H,连接CM,
在Rt△ABC中,AB==5,
S△ABC=AC·BC=AB·CH,即×3×4=×5CH,解得CH=.
∵点D,E分别为CN,MN的中点,
∴DE是△MNC的中位线,∴DE=CM,
当CM⊥AB时,CM最小,最小值为,
∴DE的最小值为.
类型二
4.如图W4-4,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF= .
图W4-4
1
[解析]∵DE为△ABC的中位线,∠AFB=90°,
∴DE=BC,DF=AB,
∵AB=6,BC=8,∴DE=×8=4,DF=×6=3,
∴EF=DE-DF=4-3=1.
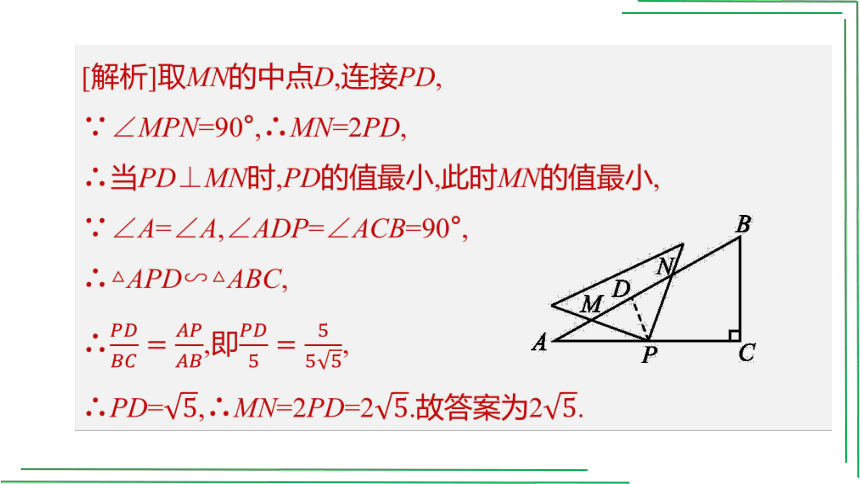
5.如图W4-5,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,将直角三角板的直角顶点与AC边的中点P重合,直角三角板绕着点P旋转,两条直角边分别交AB边于M,N,则MN的最小值是 .
图W4-5
2
[解析]取MN的中点D,连接PD,
∵∠MPN=90°,∴MN=2PD,
∴当PD⊥MN时,PD的值最小,此时MN的值最小,
∵∠A=∠A,∠ADP=∠ACB=90°,
∴△APD∽△ABC,
∴,即,
∴PD=,∴MN=2PD=2.故答案为2.
6.如图W4-6,等腰直角三角形ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为 .
图W4-6
1
[解析]如图,连接OM,CM,OC.
∵OQ⊥OP,且M是PQ的中点,∴OM=PQ.
∵△ABC是等腰直角三角形,∴∠ACB=90°,
∴CM=PQ,∴OM=CM,
∴△OCM是等腰三角形,∴M在OC的垂直平分线上.
∵当P在A点时,点M为AC的中点,当P在C点时,点M为BC的中点,
∴点M所经过的路线长为AB=1.
7.已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图W4-7①,若点E,F分别为AB,AC上的点,且DE⊥DF,求证:BE=AF.
(2)若点E,F分别为AB,CA延长线上的点,且DE⊥DF,那么BE=
AF吗 请利用图②说明理由.
图W4-7
(1)如图W4-7①,若点E,F分别为AB,AC上的点,且DE⊥DF,求证:BE=AF.
图W4-7
解:(1)证明:如图①,连接AD.
∵∠BAC=90°,AB=AC,D为BC的中点,
∴∠BDA=∠EDF=90°,
∴∠BDE+∠EDA=∠EDA+∠ADF.
∴∠BDE=∠ADF.
又∵D为BC的中点,△ABC是等腰直角三角形,
∴BD=AD,∠B=∠DAC=45°.
∴△BDE≌△ADF(ASA).∴BE=AF.
(2)若点E,F分别为AB,CA延长线上的点,且DE⊥DF,那么BE=AF吗 请利用图②说明理由.
图W4-7
(2)BE=AF.理由:如图②,连接AD.
∵∠BDA=∠EDF=90°,
∴∠BDE+∠BDF=∠BDF+∠ADF.
∴∠BDE=∠ADF.
又∵D为BC的中点,△ABC是等腰直角三角形,
∴BD=AD,∠ABC=∠DAC=45°.
∴∠EBD=∠FAD=180°-45°=135°.∴△BDE≌△ADF(ASA).∴BE=AF.
类型三
8.如图W4-8,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3,则AC的长为 ( )
A.12 B.14 C.16 D.18
图W4-8
B
9.[2020·苏州]如图W4-9,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= .
图W4-9
1
[解析]取BD中点F,连接EF,
∵BD=2CD,∴FD=CD,
∵AD⊥BC,∴EF=CE.
∵E是AD的中点,
∴EF为△ABD的中位线,∴EF=EC=AB=1.
10.如图W4-10,在△ABC中,AB=5,AC=3,AD,AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连接DH,则线段DH的长为 .
图W4-10
1
10.1
[解析]∵AE为△ABC的角平分线,CH⊥AE,
∴△ACF是等腰三角形,∴AF=AC.
∵AC=3,∴AF=AC=3,HF=CH.
∵AD为△ABC的中线,
∴DH是△BCF的中位线,
∴DH=BF,∵AB=5,∴BF=AB-AF=5-3=2.
∴DH=1.
类型四
11.[2019·临沂]如图W4-11,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是 .
图W4-11
8
[解析]∵DC⊥BC,∴∠BCD=90°,
∵∠ACB=120°,∴∠ACD=30°,
如图,延长CD到H使DH=CD,连接AH.
∵D为AB的中点,∴AD=BD,
在△ADH与△BDC中,
∴△ADH≌△BDC(SAS),
∴AH=BC=4,∠H=∠BCD=90°,
∵∠ACH=30°,∴CH=AH=4,
∴CD=2,
∴△ABC的面积=2S△BCD=2××4×2=8,
故答案为:8.
12.[2020·自贡改编]如图W4-12,在平行四边形ABCD中,AD=2,
AB=,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF.若∠EFD=90°,则AE长为 .
图W4-12
[解析]如图,延长EF交DA的延长线于Q,连接DE,设BE=x.
∵四边形ABCD是平行四边形,
∴DQ∥BC,∴∠Q=∠BEF,
∵AF=FB,∠AFQ=∠BFE,
∴△QFA≌△EFB(AAS),
∴AQ=BE=x,QF=EF,
∵∠EFD=90°,∴DF⊥QE,∴DQ=DE=x+2,
∵AE⊥BC,BC∥AD,∴AE⊥AD,
∴∠AEB=∠EAD=90°,
∵AE2=DE2-AD2=AB2-BE2,
∴(x+2)2-4=6-x2,
整理得:2x2+4x-6=0,
解得x=1或x=-3(舍去),∴BE=1,
∴AE=.
13.如图W4-13,在△ABC中,∠ACB=90°,M为AB的中点,∠PMQ=
90°,试判断线段PQ,AP,BQ之间的数量关系,并说明理由.
图W4-13
解:BQ2+AP2=PQ2,理由如下:
方法一:如图,延长PM至D,使得MD=PM,
连接BD,QD,易证△AMP≌△BMD,
∴AP=BD,∠CBD=90°,∴BQ2+BD2=DQ2,
∵∠PMQ=90°,∴PQ=DQ,
∴BQ2+AP2=PQ2.
方法二:如图,作点A关于PM的对称点A',连接A'P,A'M,A'Q.
易知∠AMP=∠A'MP.
∵∠PMQ=90°,
∴∠A'MP+∠A'MQ=90°,
∠AMP+∠BMQ=90°,
∴∠A'MQ=∠BMQ.
在△A'MQ和△BMQ中,
A'M=AM=BM,∠A'MQ=∠BMQ,MQ=MQ,
∴△A'MQ≌△BMQ,
∴∠B=∠MA'Q,A'Q=BQ,∠A=∠PA'M.
∵∠A+∠B=90°,∴∠PA'Q=90°,
∴A'P2+A'Q2=PQ2,
∴BQ2+AP2=PQ2.
14.如图W4-14所示,在△ABC中,∠ABC的平分线BE与BC边上的中线AD垂直,垂足为G,已知BE=AD=4,则AC= .
综合训练
图W4-14
3
[解析]思路提示:由于D,G为BC,AD中点,如图①②③④⑤分别以D,B,C三点构造平行线.
方法一:如图①,取CE的中点F,连接DF,
∵AD是△ABC的中线,∴BD=CD,
∴DF是△BCE的中位线,
∴DF∥BE,DF=BE=×4=2.
∵BE是∠ABC的平分线,BE⊥AD,
∴AG=GD=AD=×4=2,AB=BD,
∴GE是△ADF的中位线,∴GE=DF=×2=1,
∵BE=4,∴BG=BE-GE=4-1=3,
在Rt△AEG中,AE=.
∵DF是△BCE的中位线,GE是△ADF的中位线,
∴AE=EF=CF=,
∴AC=3.
方法二:如图②,延长AD至点F,使DF=GD,连接FC,
易证△BGD≌△CFD,∴BG=CF,FC∥BG.
由AG=AF,得GE=FC.
由GE+BG=4,得GE+FC=4,得GE=1,∴AE=,AC=3.
方法三:如图③,延长CA至点F,使AF=AC,易得FB∥AD,
∵AF=AC,CD=DB,∴BF=2AD=8,
故EF=4.
又,∴AE=,∴AC=AF=3.
其余方法可参照图④⑤所作辅助线进行求解,
也可以过A,G,D三点构造平行线,
如图所示,同学们可自己尝试求解.
15.如图W4-15,在正方形ABCD中,G为AB边的中点,E,F分别为AD,BC边上的点,若AE=1,BF=2,∠EGF=90°,则EF的长为
.
图W4-15
3
[解析]方法一:如图①,延长EG,
交CB延长线于点H.
易证△EGA≌△HGB,
∴AE=BH=1,GE=GH.
∵∠EGF=90°,∴FE=FH=3.
方法二:如图②,过G作GN∥AE交EF于点N,过点G作GH⊥EF于H.
∵GN∥AE,AG=GB,∴EN=NF,∠AEG=∠EGN.
又∵∠EGF=90°,
∴EN=NG,∴∠EGN=∠NEG,
∴∠AEG=∠GEN.
易证△EAG≌△EHG,∴EH=EA=1.
同理△GBF≌△GHF,∴FH=FB=2.
∴EF=EH+FH=3.
16.[2020·河南]如图W4-16,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 .
图W4-16
1
[解析]方法一:如图,连接CH并延长交AD边于点M,连接EM.
∵四边形ABCD为正方形,∴AD∥BC,
∴∠MDH=∠CFH,∠DMH=∠FCH,
∵H是DF的中点,
∴DH=FH,
∴△DMH≌△FCH,
∴DM=CF,MH=CH.
∵F是BC的中点,E是AB的中点,AB=CB=2,
∴CF=,AE=,
∴DM=,AM=,
∴ME==2.
∵G是EC的中点,H是CM的中点,
∴GH=ME=1.
方法二:思路提示:如图,连接EH并延长至M,
使得HM=EH,连接CM.究其本质,等价于作
CM∥GH.
方法三:思路提示:如图,连接FG并延长,交AD于点N,取FN中点M,连接DM.究其本质,等价于作DM∥GH.
方法四:思路提示:如图,连接DG并延长,交AB延长线于点M,连接FM.究其本质,等价于作FM∥GH.
17.[2019·甘肃]如图W4-17,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,证明:AB=FB.
图W4-17
(1)证明:△ADG≌△DCE;
图W4-17
证明:(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA).
(2)连接BF,证明:AB=FB.
图W4-17
(2)方法一:如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
方法二:如图所示,取AD中点H,连接BH,FH.
∵E是BC的中点,∴BE=CE=,
同理DH=AH=,∴BE=DH,
∴四边形BEDH为平行四边形,
∴BH∥ED,又AG⊥ED,∴BH⊥AG.
又∵在Rt△AFD中,H为AD中点,∴FH=AH.
∴BH是线段AF的垂直平分线,∴AB=BF.
18.如图W4-18,在五边形ABCDE中,∠ABC=∠AED=90°,∠BAC=
∠EAD,F为CD的中点.求证:BF=EF.
图W4-18
证明:方法一:分别取AC,AD的中点H,G,
连接BH,FH,GF,GE,如图,
∵∠ABC=∠AED=90°,
∴BH=HA=AC,EG=GA=AD,
∴∠BAH=∠ABH,∠GAE=∠GEA,
∴∠BHC=2∠BAC,∠EGD=2∠EAD,
而∠BAC=∠EAD,∴∠BHC=∠EGD,
又∵F是CD中点,H是AC的中点,G是AD的中点,
∴FH,GF是△CAD的中位线,
∴FH=AD,FH∥AD,GF=AC,GF∥AC,
∴∠CHF=∠CAD,∠DGF=∠DAC,FH=EG,GF=BH,
∴∠BHC+∠CHF=∠EGD+∠DGF,即∠BHF=∠EGF,
在△BHF和△FGE中,∴△BHF≌△FGE,∴BF=EF.
方法二:延长CB到C',使BC'=BC,连接AC',C'D.
延长DE到D',使D'E=DE,连接AD',CD',如图.
易证△AC'D≌△ACD'.
故C'D=CD'.
故BF=EF.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
提分微课 04
关于中点的联想
解答中点问题的关键是通过联想恰当地添加辅助线,如构造三角形中位线、作直角三角形斜边上的中线、作倍长中线、构造中心对称图形等.
类型一
1.如图W4-1,AB是☉O的直径,点C是☉O上的一点,连接AC,BC,
OD⊥BC于点D,AC=6,则OD的长为 ( )
A.2 B.3 C. D.4
图W4-1
B
2.如图W4-2,在△ABC中,延长BC至D,使得CD=BC,过AC的中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为 ( )
A.3 B.4
C.2 D.3
图W4-2
B
[解析]如图,取BC的中点G,连接EG,
∵E是AC的中点,∴EG是△ABC的中位线,
∴EG=AB=×8=4,
设CD=x,则EF=BC=2x,
∴BG=CG=x,∴EF=2x=DG,
∵EF∥CD,∴四边形EGDF是平行四边形,
∴DF=EG=4,故选B.
3.如图W4-3,在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D,E分别为CN,MN的中点,则DE
的最小值为 .
图W4-3
[解析]如图,过C作CH⊥AB于H,连接CM,
在Rt△ABC中,AB==5,
S△ABC=AC·BC=AB·CH,即×3×4=×5CH,解得CH=.
∵点D,E分别为CN,MN的中点,
∴DE是△MNC的中位线,∴DE=CM,
当CM⊥AB时,CM最小,最小值为,
∴DE的最小值为.
类型二
4.如图W4-4,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF= .
图W4-4
1
[解析]∵DE为△ABC的中位线,∠AFB=90°,
∴DE=BC,DF=AB,
∵AB=6,BC=8,∴DE=×8=4,DF=×6=3,
∴EF=DE-DF=4-3=1.
5.如图W4-5,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,将直角三角板的直角顶点与AC边的中点P重合,直角三角板绕着点P旋转,两条直角边分别交AB边于M,N,则MN的最小值是 .
图W4-5
2
[解析]取MN的中点D,连接PD,
∵∠MPN=90°,∴MN=2PD,
∴当PD⊥MN时,PD的值最小,此时MN的值最小,
∵∠A=∠A,∠ADP=∠ACB=90°,
∴△APD∽△ABC,
∴,即,
∴PD=,∴MN=2PD=2.故答案为2.
6.如图W4-6,等腰直角三角形ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为 .
图W4-6
1
[解析]如图,连接OM,CM,OC.
∵OQ⊥OP,且M是PQ的中点,∴OM=PQ.
∵△ABC是等腰直角三角形,∴∠ACB=90°,
∴CM=PQ,∴OM=CM,
∴△OCM是等腰三角形,∴M在OC的垂直平分线上.
∵当P在A点时,点M为AC的中点,当P在C点时,点M为BC的中点,
∴点M所经过的路线长为AB=1.
7.已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图W4-7①,若点E,F分别为AB,AC上的点,且DE⊥DF,求证:BE=AF.
(2)若点E,F分别为AB,CA延长线上的点,且DE⊥DF,那么BE=
AF吗 请利用图②说明理由.
图W4-7
(1)如图W4-7①,若点E,F分别为AB,AC上的点,且DE⊥DF,求证:BE=AF.
图W4-7
解:(1)证明:如图①,连接AD.
∵∠BAC=90°,AB=AC,D为BC的中点,
∴∠BDA=∠EDF=90°,
∴∠BDE+∠EDA=∠EDA+∠ADF.
∴∠BDE=∠ADF.
又∵D为BC的中点,△ABC是等腰直角三角形,
∴BD=AD,∠B=∠DAC=45°.
∴△BDE≌△ADF(ASA).∴BE=AF.
(2)若点E,F分别为AB,CA延长线上的点,且DE⊥DF,那么BE=AF吗 请利用图②说明理由.
图W4-7
(2)BE=AF.理由:如图②,连接AD.
∵∠BDA=∠EDF=90°,
∴∠BDE+∠BDF=∠BDF+∠ADF.
∴∠BDE=∠ADF.
又∵D为BC的中点,△ABC是等腰直角三角形,
∴BD=AD,∠ABC=∠DAC=45°.
∴∠EBD=∠FAD=180°-45°=135°.∴△BDE≌△ADF(ASA).∴BE=AF.
类型三
8.如图W4-8,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3,则AC的长为 ( )
A.12 B.14 C.16 D.18
图W4-8
B
9.[2020·苏州]如图W4-9,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= .
图W4-9
1
[解析]取BD中点F,连接EF,
∵BD=2CD,∴FD=CD,
∵AD⊥BC,∴EF=CE.
∵E是AD的中点,
∴EF为△ABD的中位线,∴EF=EC=AB=1.
10.如图W4-10,在△ABC中,AB=5,AC=3,AD,AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连接DH,则线段DH的长为 .
图W4-10
1
10.1
[解析]∵AE为△ABC的角平分线,CH⊥AE,
∴△ACF是等腰三角形,∴AF=AC.
∵AC=3,∴AF=AC=3,HF=CH.
∵AD为△ABC的中线,
∴DH是△BCF的中位线,
∴DH=BF,∵AB=5,∴BF=AB-AF=5-3=2.
∴DH=1.
类型四
11.[2019·临沂]如图W4-11,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是 .
图W4-11
8
[解析]∵DC⊥BC,∴∠BCD=90°,
∵∠ACB=120°,∴∠ACD=30°,
如图,延长CD到H使DH=CD,连接AH.
∵D为AB的中点,∴AD=BD,
在△ADH与△BDC中,
∴△ADH≌△BDC(SAS),
∴AH=BC=4,∠H=∠BCD=90°,
∵∠ACH=30°,∴CH=AH=4,
∴CD=2,
∴△ABC的面积=2S△BCD=2××4×2=8,
故答案为:8.
12.[2020·自贡改编]如图W4-12,在平行四边形ABCD中,AD=2,
AB=,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF.若∠EFD=90°,则AE长为 .
图W4-12
[解析]如图,延长EF交DA的延长线于Q,连接DE,设BE=x.
∵四边形ABCD是平行四边形,
∴DQ∥BC,∴∠Q=∠BEF,
∵AF=FB,∠AFQ=∠BFE,
∴△QFA≌△EFB(AAS),
∴AQ=BE=x,QF=EF,
∵∠EFD=90°,∴DF⊥QE,∴DQ=DE=x+2,
∵AE⊥BC,BC∥AD,∴AE⊥AD,
∴∠AEB=∠EAD=90°,
∵AE2=DE2-AD2=AB2-BE2,
∴(x+2)2-4=6-x2,
整理得:2x2+4x-6=0,
解得x=1或x=-3(舍去),∴BE=1,
∴AE=.
13.如图W4-13,在△ABC中,∠ACB=90°,M为AB的中点,∠PMQ=
90°,试判断线段PQ,AP,BQ之间的数量关系,并说明理由.
图W4-13
解:BQ2+AP2=PQ2,理由如下:
方法一:如图,延长PM至D,使得MD=PM,
连接BD,QD,易证△AMP≌△BMD,
∴AP=BD,∠CBD=90°,∴BQ2+BD2=DQ2,
∵∠PMQ=90°,∴PQ=DQ,
∴BQ2+AP2=PQ2.
方法二:如图,作点A关于PM的对称点A',连接A'P,A'M,A'Q.
易知∠AMP=∠A'MP.
∵∠PMQ=90°,
∴∠A'MP+∠A'MQ=90°,
∠AMP+∠BMQ=90°,
∴∠A'MQ=∠BMQ.
在△A'MQ和△BMQ中,
A'M=AM=BM,∠A'MQ=∠BMQ,MQ=MQ,
∴△A'MQ≌△BMQ,
∴∠B=∠MA'Q,A'Q=BQ,∠A=∠PA'M.
∵∠A+∠B=90°,∴∠PA'Q=90°,
∴A'P2+A'Q2=PQ2,
∴BQ2+AP2=PQ2.
14.如图W4-14所示,在△ABC中,∠ABC的平分线BE与BC边上的中线AD垂直,垂足为G,已知BE=AD=4,则AC= .
综合训练
图W4-14
3
[解析]思路提示:由于D,G为BC,AD中点,如图①②③④⑤分别以D,B,C三点构造平行线.
方法一:如图①,取CE的中点F,连接DF,
∵AD是△ABC的中线,∴BD=CD,
∴DF是△BCE的中位线,
∴DF∥BE,DF=BE=×4=2.
∵BE是∠ABC的平分线,BE⊥AD,
∴AG=GD=AD=×4=2,AB=BD,
∴GE是△ADF的中位线,∴GE=DF=×2=1,
∵BE=4,∴BG=BE-GE=4-1=3,
在Rt△AEG中,AE=.
∵DF是△BCE的中位线,GE是△ADF的中位线,
∴AE=EF=CF=,
∴AC=3.
方法二:如图②,延长AD至点F,使DF=GD,连接FC,
易证△BGD≌△CFD,∴BG=CF,FC∥BG.
由AG=AF,得GE=FC.
由GE+BG=4,得GE+FC=4,得GE=1,∴AE=,AC=3.
方法三:如图③,延长CA至点F,使AF=AC,易得FB∥AD,
∵AF=AC,CD=DB,∴BF=2AD=8,
故EF=4.
又,∴AE=,∴AC=AF=3.
其余方法可参照图④⑤所作辅助线进行求解,
也可以过A,G,D三点构造平行线,
如图所示,同学们可自己尝试求解.
15.如图W4-15,在正方形ABCD中,G为AB边的中点,E,F分别为AD,BC边上的点,若AE=1,BF=2,∠EGF=90°,则EF的长为
.
图W4-15
3
[解析]方法一:如图①,延长EG,
交CB延长线于点H.
易证△EGA≌△HGB,
∴AE=BH=1,GE=GH.
∵∠EGF=90°,∴FE=FH=3.
方法二:如图②,过G作GN∥AE交EF于点N,过点G作GH⊥EF于H.
∵GN∥AE,AG=GB,∴EN=NF,∠AEG=∠EGN.
又∵∠EGF=90°,
∴EN=NG,∴∠EGN=∠NEG,
∴∠AEG=∠GEN.
易证△EAG≌△EHG,∴EH=EA=1.
同理△GBF≌△GHF,∴FH=FB=2.
∴EF=EH+FH=3.
16.[2020·河南]如图W4-16,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 .
图W4-16
1
[解析]方法一:如图,连接CH并延长交AD边于点M,连接EM.
∵四边形ABCD为正方形,∴AD∥BC,
∴∠MDH=∠CFH,∠DMH=∠FCH,
∵H是DF的中点,
∴DH=FH,
∴△DMH≌△FCH,
∴DM=CF,MH=CH.
∵F是BC的中点,E是AB的中点,AB=CB=2,
∴CF=,AE=,
∴DM=,AM=,
∴ME==2.
∵G是EC的中点,H是CM的中点,
∴GH=ME=1.
方法二:思路提示:如图,连接EH并延长至M,
使得HM=EH,连接CM.究其本质,等价于作
CM∥GH.
方法三:思路提示:如图,连接FG并延长,交AD于点N,取FN中点M,连接DM.究其本质,等价于作DM∥GH.
方法四:思路提示:如图,连接DG并延长,交AB延长线于点M,连接FM.究其本质,等价于作FM∥GH.
17.[2019·甘肃]如图W4-17,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE;
(2)连接BF,证明:AB=FB.
图W4-17
(1)证明:△ADG≌△DCE;
图W4-17
证明:(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA).
(2)连接BF,证明:AB=FB.
图W4-17
(2)方法一:如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=AH=AB.
方法二:如图所示,取AD中点H,连接BH,FH.
∵E是BC的中点,∴BE=CE=,
同理DH=AH=,∴BE=DH,
∴四边形BEDH为平行四边形,
∴BH∥ED,又AG⊥ED,∴BH⊥AG.
又∵在Rt△AFD中,H为AD中点,∴FH=AH.
∴BH是线段AF的垂直平分线,∴AB=BF.
18.如图W4-18,在五边形ABCDE中,∠ABC=∠AED=90°,∠BAC=
∠EAD,F为CD的中点.求证:BF=EF.
图W4-18
证明:方法一:分别取AC,AD的中点H,G,
连接BH,FH,GF,GE,如图,
∵∠ABC=∠AED=90°,
∴BH=HA=AC,EG=GA=AD,
∴∠BAH=∠ABH,∠GAE=∠GEA,
∴∠BHC=2∠BAC,∠EGD=2∠EAD,
而∠BAC=∠EAD,∴∠BHC=∠EGD,
又∵F是CD中点,H是AC的中点,G是AD的中点,
∴FH,GF是△CAD的中位线,
∴FH=AD,FH∥AD,GF=AC,GF∥AC,
∴∠CHF=∠CAD,∠DGF=∠DAC,FH=EG,GF=BH,
∴∠BHC+∠CHF=∠EGD+∠DGF,即∠BHF=∠EGF,
在△BHF和△FGE中,∴△BHF≌△FGE,∴BF=EF.
方法二:延长CB到C',使BC'=BC,连接AC',C'D.
延长DE到D',使D'E=DE,连接AD',CD',如图.
易证△AC'D≌△ACD'.
故C'D=CD'.
故BF=EF.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
