2022中考数学三轮冲刺考前提分微课03 关于角平分线的联想 课件(共41张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课03 关于角平分线的联想 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:11:03 | ||
图片预览










文档简介
(共41张PPT)
2022年中考数学三轮复习(人教版)
提分微课 03
关于角平分线的联想
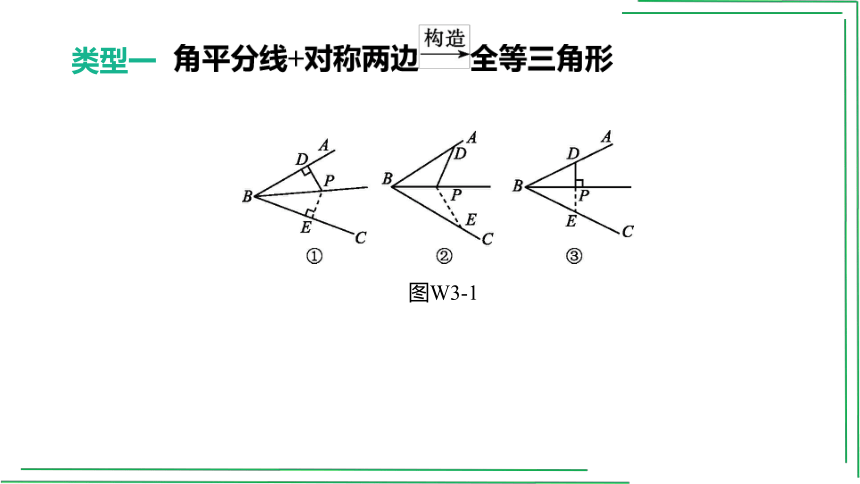
类型一
图W3-1
例1 如图W3-2,半圆O的直径AB=5,AC,AD为弦,若AC=3,AD平分∠BAC,求AD的长.
图W3-2
[思路分析1]
遇角平分线上一点,可以作双垂直构造全等三角形,结合三角形全等与相似求解.
解:解法1:(双垂直法)
过D作DG⊥AB于点G,过点D作DH⊥AC
交AC的延长线于点H,连接DB,DC.
由AD平分∠BAC可得DG=DH,BD=DC,
∴Rt△BDG≌Rt△CDH,∴BG=CH.
设BG=CH=x,则AH=3+x,AG=5-x.
易证△ADH≌△ADG,∴AH=AG,
∴3+x=5-x,∴x=1.∴BG=1,AG=4.
∵∠DAG=∠BAD,∠AGD=∠BDA=90°,
∴△ADG∽△ABD,∴,
∴AD2=AG·AB=4×5=20,∴AD=2.
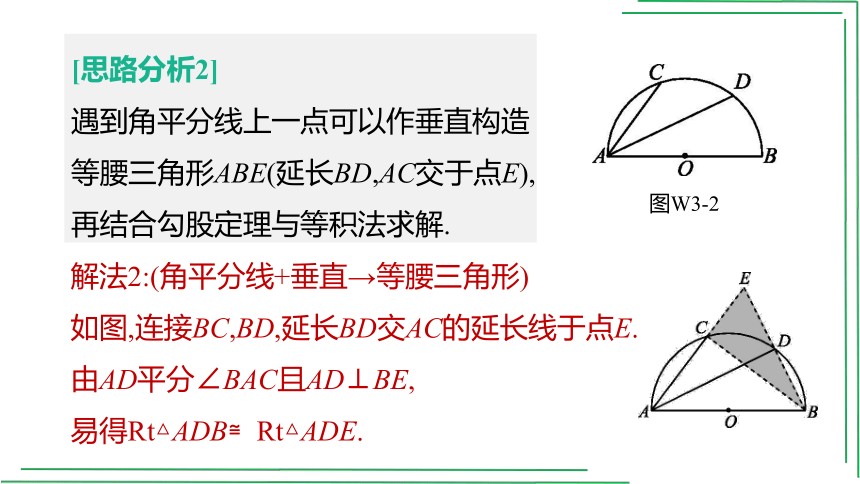
[思路分析2]
遇到角平分线上一点可以作垂直构造等腰三角形ABE(延长BD,AC交于点E),
再结合勾股定理与等积法求解.
图W3-2
解法2:(角平分线+垂直→等腰三角形)
如图,连接BC,BD,延长BD交AC的延长线于点E.
由AD平分∠BAC且AD⊥BE,
易得Rt△ADB≌Rt△ADE.
则AE=AB=5,CE=2,BC=4,
易得∠BCE=90°,
在Rt△BCE中,
BE==2.
S△ABE=AE·BC=BE·AD,
∴×5×4=×2×AD,∴AD=2.
巩固训练
1.如图W3-3,BD是∠ABC的平分线,DE⊥AB于E,△ABC的面积是50 cm2,AB=11 cm,BC=14 cm,则DE= cm.
图W3-3
4
[解析]如图,过点D作DF⊥BC于点F,
∵BD是∠ABC的平分线,DE⊥AB,
∴DF=DE.
∵△ABC的面积是50,AB=11,BC=14,
∴BC·DF+AB·DE=50,
∴×14×DF+×11×DE=50,
∴DE=4.
2.如图W3-4,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点B的坐标为 ;AC的长度为 .
(2)若CD平分∠ACO,交x轴于点D,则直线CD的函数表达式为 .
图W3-4
(12,9)
15
y=-2x+9
[解析](1)∵四边形OABC是矩形,
∴AB=OC=9,BC=OA=12,
∴A(12,0),B(12,9),AC==15.
故答案为(12,9);15.
(2)如图,作DM⊥AC于M.
∵CD平分∠ACO,DO⊥CO,DM⊥AC,
∴DO=DM,∠COD=∠CMD=90°,
∵CD=CD,∴Rt△CDO≌Rt△CDM(HL),∴CM=OC=9.
∵AC=15,∴AM=6.
设OD=x,则DM=x,AD=12-x,
在Rt△ADM中,∵AD2=DM2+AM2,
∴x2+62=(12-x)2,解得x=,∴D(,0).
设直线CD的解析式为y=kx+b,代入C(0,9),D(,0),
则解得
∴直线CD的解析式为y=-2x+9.
3.如图W3-5,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB=
AC+CD.
图W3-5
证法一:如图,在AB上截取AF,使AF=AC.
∵AD平分∠BAC,∴∠1=∠2,
在△AFD与△ACD中,
∴△AFD≌△ACD(SAS),
∴DF=DC,∠AFD=∠C,
∵∠C=2∠B,∠AFD=∠3+∠B,
∴∠3=∠B,∴FD=FB.
∵AB=AF+FB=AC+FD,∴AB=AC+CD.
证法二:如图,延长AC到点E,使CE=DC.
∴∠CDE=∠CED,∴∠ACB=2∠CED,
又∵∠ACB=2∠B,
∴∠B=∠CED,
∵AD平分∠BAC,
∴∠1=∠2,
在△ABD与△AED中,
∴△ABD≌△AED(AAS),∴AB=AE.
又∵AE=AC+CE=AC+DC,
∴AB=AC+DC.
类型二
图W3-6
例2 如图W3-7,矩形ABCD中,BC=6,E为CD上一点,CE=2,DE=1,将矩形ABCD沿BE折叠,G是C的对应点,BG与AD交于点F,求AF的长.
图W3-7
[思路分析1]
过点E作EM∥BG交BC于点M,由BE平分∠FBC构造等腰三角形MBE,利用勾股定理求MC,再结合△MCE∽△FAB即可求得AF的长.
解:解法1:如图①,过点E作EM∥BG交BC于点M,
设MC=x,则BM=6-x.
∵∠MBE=∠EBF,∠MEB=∠EBF(易得),
∴∠MBE=∠MEB,∴MB=ME=6-x.
在Rt△MCE中,MC2+CE2=ME2,∴x2+22=(6-x)2,解得x=.
∵∠EMC=2∠MBE,∠BFA=∠FBC=2∠MBE,
∴∠EMC=∠BFA,∴△MCE∽△FAB,
∴,即,∴AF=4.
[思路分析2]
延长BE交AD延长线于点H,构造△HDE∽△BCE,利用平行线性质,结合折叠可知△BFH是等腰三角形,再利用勾股定理即可求得AF的长.
解法2:如图②,延长BE交AD延长线于点H,则△HDE∽△BCE,
∴,即,∴HD=3.
∵AH∥BC,∴∠H=∠EBC=∠EBF,
∴BF=FH.
图W3-7
设AF=x,
∵AH=AD+DH=6+3=9,
∴BF=FH=9-x,
在Rt△ABF中,AF2+AB2=BF2,
∴x2+32=(9-x)2,
解得x=4,即AF=4.
[思路分析3]
延长EG交BA的延长线于点H,发现△HBE是等腰三角形,利用△HGB是直角三角形,由勾股定理求出HG的长度,由△ABF∽
△GBH求出AF的长.
图W3-8
解法3:延长EG交BA的延长线于点H,如图③,
∵∠BEG=∠BEC=∠EBH,∴∠BEG=∠EBH,∴HB=HE,
设HG=x,
由折叠知EG=EC=2,BG=BC=6,则HB=HE=x+2,
在Rt△HBG中,HG2+BG2=BH2,
∴x2+62=(x+2)2,解得x=8.
∵∠ABF=∠GBH,∠FAB=∠BGH=90°,
∴△ABF∽△GBH,∴,即,
∴AF=4.
巩固训练
4.如图W3-9,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE= .
图W3-9
3
[解析]∵AC是正方形ABCD的对角线,AB=3,
∴AC=3,
∵∠DCA的平分线交BA的延长线于点E,
∴∠DCE=∠ECA.
∵DC∥EB,∴∠CEA=∠DCE,
∴∠CEA=∠ECA,∴AE=AC=3,
故答案为:3.
5.如图W3-10,点P是∠AOB的平分线上一点,过点P作PC∥OA交OB于点C,过点P作PD⊥OA于点D,若∠AOB=60°,OC=4,则PD= .
图W3-10
2
[解析]∵∠AOB=60°,点P是∠AOB的平分线上一点,
∴∠POD=∠POC=30°,
又∵PC∥OA,∴∠PCB=∠AOB=60°,
∴∠PCO=180°-60°=120°,∠POC=∠OPC=30°,
∴PC=OC.
过点P作PE⊥OB于点E.∵OC=4,∠PCE=60°,
∴PC=4,CE=2,PE==2,∴PD=2.
故答案为2.
6.在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
8或3
[解析]①如图①,在 ABCD中,∵BC∥AD,∴∠ADF=∠CFD.
∵DF平分∠ADC交BC于点F,
∴∠ADF=∠CDF,∴∠CFD=∠CDF,∴CF=CD.
同理可证AB=BE.∴AB=BE=CF=CD.
∵EF=5,BC=AD=11,
∴BC=BE+CF-EF=2AB-EF=2AB-5=11,
∴AB=8.
①
②如图②,在 ABCD中,
同①可得AB=BE=CF=CD,
∵EF=5,
∴BC=BE+CF+EF=2AB+EF=2AB+5=11,
∴AB=3.故答案为8或3.
②
7.如图W3-11,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=
∠ABD,若AC=8,BC=5,则BD的长为 .
图W3-11
1.5
[解析]如图,延长BD与AC交于点E,
∵∠A=∠ABD,∴BE=AE.
∵BD⊥CD,∴BE⊥CD,
∵CD平分∠ACB,∴∠ECD=∠BCD,
∴△BEC为等腰三角形,∴BC=CE.
∵BE⊥CD,∴2BD=BE,
∵AC=8,BC=5,∴CE=5,AE=AC-EC=8-5=3,
∴BE=3,∴BD=1.5.
8.如图W3-12,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于点E,BD⊥AD,若BD=2,则AE= .
图W3-12
4
[解析]延长BD,AC交于点F,
∵AD平分∠BAC,AD⊥BD,
∴∠ABF=∠AFB,BD=FD,BF=2BD.
∵AD⊥BD,∠ACB=90°,∠AEC=∠BED,
∴∠EAC=∠FBC.
又∵AC=BC,∴△ACE≌△BCF,
∴AE=BF=2BD=4.
9.如图W3-13,△ABC中,∠BAC=90°,S△ABC=10,AD平分∠BAC,交BC于点D,BE⊥AD交AD延长线于点E,连接CE,则△ACE的面积为 .
图W3-13
5
[解析]延长BE和AC交于点F,易得△ABF是等腰直角三角形.
∵AE⊥BF,∴BE=EF.
∴S△ACE=S△AEF-S△CEF=S△ABF-S△BCF=(S△ABF-S△BCF)=S△ABC=5.
10.如图W3-14,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于点G.
求证:BF=AC+AF.
图W3-14
证明:延长FE至Q,使EQ=EF,连接CQ,
如图所示.
∵E为BC边的中点,
∴BE=CE,
在△BEF和△CEQ中,
∵
∴△BEF≌△CEQ(SAS),
∴BF=CQ,∠BFE=∠Q.
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∵EF∥AD,
∴∠CAD=∠G,∠BAD=∠BFE=∠GFA,
∴∠G=∠GFA,∴AG=AF.
∵∠BFE=∠Q,
∴∠G=∠Q,∴CQ=CG,
∵CQ=BF,
∴BF=CG=AG+AC=AF+AC.
类型三
图W3-15
如图W3-15,三角形任意两条角平分线交于点P,则点P为三角形的内心,且S△ABC=(AB+AC+BC)·PM,∠BPC=90°+∠A.
11.如图W3-16所示,△ABC的三边AB,BC,CA的长分别是20,30,
40,三条角平分线将△ABC分为3个三角形,则S△OAB∶S△OBC∶S△OAC= .
巩固训练
图W3-16
2∶3∶4
12.如图W3-17所示,已知△ABC的周长是18 cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若△ABC的面积为45 cm2,则OD= ;若∠BOC=110°,则∠A= °.
图W3-17
5 cm
40
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
提分微课 03
关于角平分线的联想
类型一
图W3-1
例1 如图W3-2,半圆O的直径AB=5,AC,AD为弦,若AC=3,AD平分∠BAC,求AD的长.
图W3-2
[思路分析1]
遇角平分线上一点,可以作双垂直构造全等三角形,结合三角形全等与相似求解.
解:解法1:(双垂直法)
过D作DG⊥AB于点G,过点D作DH⊥AC
交AC的延长线于点H,连接DB,DC.
由AD平分∠BAC可得DG=DH,BD=DC,
∴Rt△BDG≌Rt△CDH,∴BG=CH.
设BG=CH=x,则AH=3+x,AG=5-x.
易证△ADH≌△ADG,∴AH=AG,
∴3+x=5-x,∴x=1.∴BG=1,AG=4.
∵∠DAG=∠BAD,∠AGD=∠BDA=90°,
∴△ADG∽△ABD,∴,
∴AD2=AG·AB=4×5=20,∴AD=2.
[思路分析2]
遇到角平分线上一点可以作垂直构造等腰三角形ABE(延长BD,AC交于点E),
再结合勾股定理与等积法求解.
图W3-2
解法2:(角平分线+垂直→等腰三角形)
如图,连接BC,BD,延长BD交AC的延长线于点E.
由AD平分∠BAC且AD⊥BE,
易得Rt△ADB≌Rt△ADE.
则AE=AB=5,CE=2,BC=4,
易得∠BCE=90°,
在Rt△BCE中,
BE==2.
S△ABE=AE·BC=BE·AD,
∴×5×4=×2×AD,∴AD=2.
巩固训练
1.如图W3-3,BD是∠ABC的平分线,DE⊥AB于E,△ABC的面积是50 cm2,AB=11 cm,BC=14 cm,则DE= cm.
图W3-3
4
[解析]如图,过点D作DF⊥BC于点F,
∵BD是∠ABC的平分线,DE⊥AB,
∴DF=DE.
∵△ABC的面积是50,AB=11,BC=14,
∴BC·DF+AB·DE=50,
∴×14×DF+×11×DE=50,
∴DE=4.
2.如图W3-4,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点B的坐标为 ;AC的长度为 .
(2)若CD平分∠ACO,交x轴于点D,则直线CD的函数表达式为 .
图W3-4
(12,9)
15
y=-2x+9
[解析](1)∵四边形OABC是矩形,
∴AB=OC=9,BC=OA=12,
∴A(12,0),B(12,9),AC==15.
故答案为(12,9);15.
(2)如图,作DM⊥AC于M.
∵CD平分∠ACO,DO⊥CO,DM⊥AC,
∴DO=DM,∠COD=∠CMD=90°,
∵CD=CD,∴Rt△CDO≌Rt△CDM(HL),∴CM=OC=9.
∵AC=15,∴AM=6.
设OD=x,则DM=x,AD=12-x,
在Rt△ADM中,∵AD2=DM2+AM2,
∴x2+62=(12-x)2,解得x=,∴D(,0).
设直线CD的解析式为y=kx+b,代入C(0,9),D(,0),
则解得
∴直线CD的解析式为y=-2x+9.
3.如图W3-5,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB=
AC+CD.
图W3-5
证法一:如图,在AB上截取AF,使AF=AC.
∵AD平分∠BAC,∴∠1=∠2,
在△AFD与△ACD中,
∴△AFD≌△ACD(SAS),
∴DF=DC,∠AFD=∠C,
∵∠C=2∠B,∠AFD=∠3+∠B,
∴∠3=∠B,∴FD=FB.
∵AB=AF+FB=AC+FD,∴AB=AC+CD.
证法二:如图,延长AC到点E,使CE=DC.
∴∠CDE=∠CED,∴∠ACB=2∠CED,
又∵∠ACB=2∠B,
∴∠B=∠CED,
∵AD平分∠BAC,
∴∠1=∠2,
在△ABD与△AED中,
∴△ABD≌△AED(AAS),∴AB=AE.
又∵AE=AC+CE=AC+DC,
∴AB=AC+DC.
类型二
图W3-6
例2 如图W3-7,矩形ABCD中,BC=6,E为CD上一点,CE=2,DE=1,将矩形ABCD沿BE折叠,G是C的对应点,BG与AD交于点F,求AF的长.
图W3-7
[思路分析1]
过点E作EM∥BG交BC于点M,由BE平分∠FBC构造等腰三角形MBE,利用勾股定理求MC,再结合△MCE∽△FAB即可求得AF的长.
解:解法1:如图①,过点E作EM∥BG交BC于点M,
设MC=x,则BM=6-x.
∵∠MBE=∠EBF,∠MEB=∠EBF(易得),
∴∠MBE=∠MEB,∴MB=ME=6-x.
在Rt△MCE中,MC2+CE2=ME2,∴x2+22=(6-x)2,解得x=.
∵∠EMC=2∠MBE,∠BFA=∠FBC=2∠MBE,
∴∠EMC=∠BFA,∴△MCE∽△FAB,
∴,即,∴AF=4.
[思路分析2]
延长BE交AD延长线于点H,构造△HDE∽△BCE,利用平行线性质,结合折叠可知△BFH是等腰三角形,再利用勾股定理即可求得AF的长.
解法2:如图②,延长BE交AD延长线于点H,则△HDE∽△BCE,
∴,即,∴HD=3.
∵AH∥BC,∴∠H=∠EBC=∠EBF,
∴BF=FH.
图W3-7
设AF=x,
∵AH=AD+DH=6+3=9,
∴BF=FH=9-x,
在Rt△ABF中,AF2+AB2=BF2,
∴x2+32=(9-x)2,
解得x=4,即AF=4.
[思路分析3]
延长EG交BA的延长线于点H,发现△HBE是等腰三角形,利用△HGB是直角三角形,由勾股定理求出HG的长度,由△ABF∽
△GBH求出AF的长.
图W3-8
解法3:延长EG交BA的延长线于点H,如图③,
∵∠BEG=∠BEC=∠EBH,∴∠BEG=∠EBH,∴HB=HE,
设HG=x,
由折叠知EG=EC=2,BG=BC=6,则HB=HE=x+2,
在Rt△HBG中,HG2+BG2=BH2,
∴x2+62=(x+2)2,解得x=8.
∵∠ABF=∠GBH,∠FAB=∠BGH=90°,
∴△ABF∽△GBH,∴,即,
∴AF=4.
巩固训练
4.如图W3-9,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE= .
图W3-9
3
[解析]∵AC是正方形ABCD的对角线,AB=3,
∴AC=3,
∵∠DCA的平分线交BA的延长线于点E,
∴∠DCE=∠ECA.
∵DC∥EB,∴∠CEA=∠DCE,
∴∠CEA=∠ECA,∴AE=AC=3,
故答案为:3.
5.如图W3-10,点P是∠AOB的平分线上一点,过点P作PC∥OA交OB于点C,过点P作PD⊥OA于点D,若∠AOB=60°,OC=4,则PD= .
图W3-10
2
[解析]∵∠AOB=60°,点P是∠AOB的平分线上一点,
∴∠POD=∠POC=30°,
又∵PC∥OA,∴∠PCB=∠AOB=60°,
∴∠PCO=180°-60°=120°,∠POC=∠OPC=30°,
∴PC=OC.
过点P作PE⊥OB于点E.∵OC=4,∠PCE=60°,
∴PC=4,CE=2,PE==2,∴PD=2.
故答案为2.
6.在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .
8或3
[解析]①如图①,在 ABCD中,∵BC∥AD,∴∠ADF=∠CFD.
∵DF平分∠ADC交BC于点F,
∴∠ADF=∠CDF,∴∠CFD=∠CDF,∴CF=CD.
同理可证AB=BE.∴AB=BE=CF=CD.
∵EF=5,BC=AD=11,
∴BC=BE+CF-EF=2AB-EF=2AB-5=11,
∴AB=8.
①
②如图②,在 ABCD中,
同①可得AB=BE=CF=CD,
∵EF=5,
∴BC=BE+CF+EF=2AB+EF=2AB+5=11,
∴AB=3.故答案为8或3.
②
7.如图W3-11,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=
∠ABD,若AC=8,BC=5,则BD的长为 .
图W3-11
1.5
[解析]如图,延长BD与AC交于点E,
∵∠A=∠ABD,∴BE=AE.
∵BD⊥CD,∴BE⊥CD,
∵CD平分∠ACB,∴∠ECD=∠BCD,
∴△BEC为等腰三角形,∴BC=CE.
∵BE⊥CD,∴2BD=BE,
∵AC=8,BC=5,∴CE=5,AE=AC-EC=8-5=3,
∴BE=3,∴BD=1.5.
8.如图W3-12,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC,交BC于点E,BD⊥AD,若BD=2,则AE= .
图W3-12
4
[解析]延长BD,AC交于点F,
∵AD平分∠BAC,AD⊥BD,
∴∠ABF=∠AFB,BD=FD,BF=2BD.
∵AD⊥BD,∠ACB=90°,∠AEC=∠BED,
∴∠EAC=∠FBC.
又∵AC=BC,∴△ACE≌△BCF,
∴AE=BF=2BD=4.
9.如图W3-13,△ABC中,∠BAC=90°,S△ABC=10,AD平分∠BAC,交BC于点D,BE⊥AD交AD延长线于点E,连接CE,则△ACE的面积为 .
图W3-13
5
[解析]延长BE和AC交于点F,易得△ABF是等腰直角三角形.
∵AE⊥BF,∴BE=EF.
∴S△ACE=S△AEF-S△CEF=S△ABF-S△BCF=(S△ABF-S△BCF)=S△ABC=5.
10.如图W3-14,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于点G.
求证:BF=AC+AF.
图W3-14
证明:延长FE至Q,使EQ=EF,连接CQ,
如图所示.
∵E为BC边的中点,
∴BE=CE,
在△BEF和△CEQ中,
∵
∴△BEF≌△CEQ(SAS),
∴BF=CQ,∠BFE=∠Q.
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∵EF∥AD,
∴∠CAD=∠G,∠BAD=∠BFE=∠GFA,
∴∠G=∠GFA,∴AG=AF.
∵∠BFE=∠Q,
∴∠G=∠Q,∴CQ=CG,
∵CQ=BF,
∴BF=CG=AG+AC=AF+AC.
类型三
图W3-15
如图W3-15,三角形任意两条角平分线交于点P,则点P为三角形的内心,且S△ABC=(AB+AC+BC)·PM,∠BPC=90°+∠A.
11.如图W3-16所示,△ABC的三边AB,BC,CA的长分别是20,30,
40,三条角平分线将△ABC分为3个三角形,则S△OAB∶S△OBC∶S△OAC= .
巩固训练
图W3-16
2∶3∶4
12.如图W3-17所示,已知△ABC的周长是18 cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若△ABC的面积为45 cm2,则OD= ;若∠BOC=110°,则∠A= °.
图W3-17
5 cm
40
https://www.21cnjy.com/help/help_extract.php
同课章节目录
