2022中考数学三轮冲刺考前提分微课05 相似模型的应用 课件(共64张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课05 相似模型的应用 课件(共64张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:09:59 | ||
图片预览





文档简介
(共64张PPT)
2022年中考数学三轮复习(人教版)
提分微课 05
相似模型的应用
●构图模型
●例题精析
●巩固训练
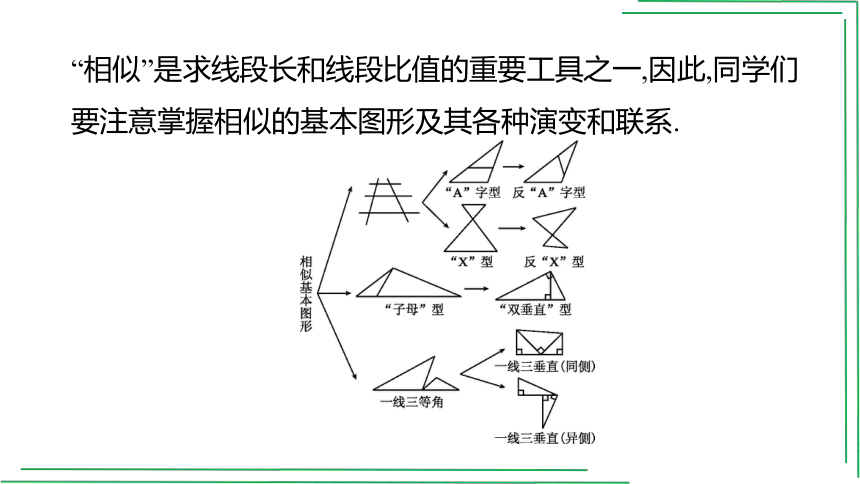
“相似”是求线段长和线段比值的重要工具之一,因此,同学们要注意掌握相似的基本图形及其各种演变和联系.
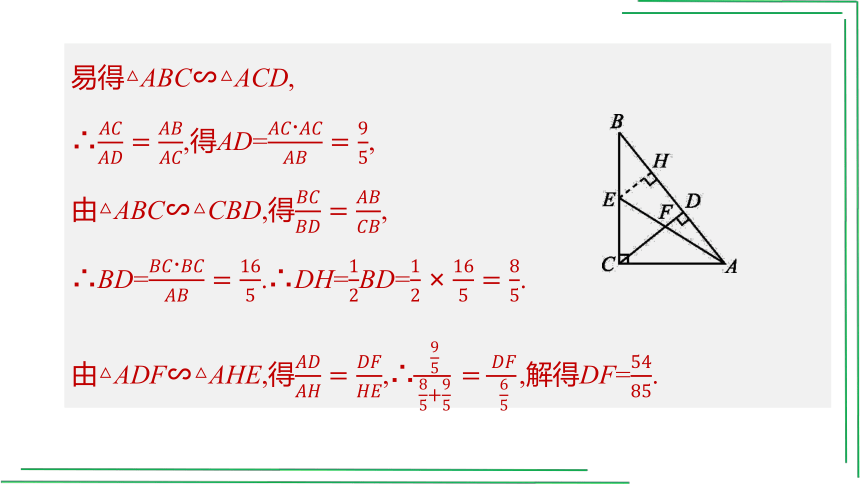
例1 [2020·山西]如图W5-1,在Rt△ABC中,∠ACB=90°,AC=3,
BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为 .
图W5-1
[思路分析]
此题易求CD的值,因此可转化为求CF,FD与CD的比例关系.
根据平行线构造A字型或X型或构造反A字型等相似图形.从而求得比例关系.
[解析]构造A字型
方法一:已知∠ACB=90°,AC=3,BC=4,由勾股定理,得AB=5.
∵CD⊥AB,
∴AB·CD=AC·BC,∴CD=.
如图,过点E作EH⊥AB于点H.则EH∥CD,
∴△BEH∽△BCD,
∴,∴EH=CD=.
易得△ABC∽△ACD,
∴,得AD=,
由△ABC∽△CBD,得,
∴BD=.∴DH=BD=.
由△ADF∽△AHE,得,∴,解得DF=.
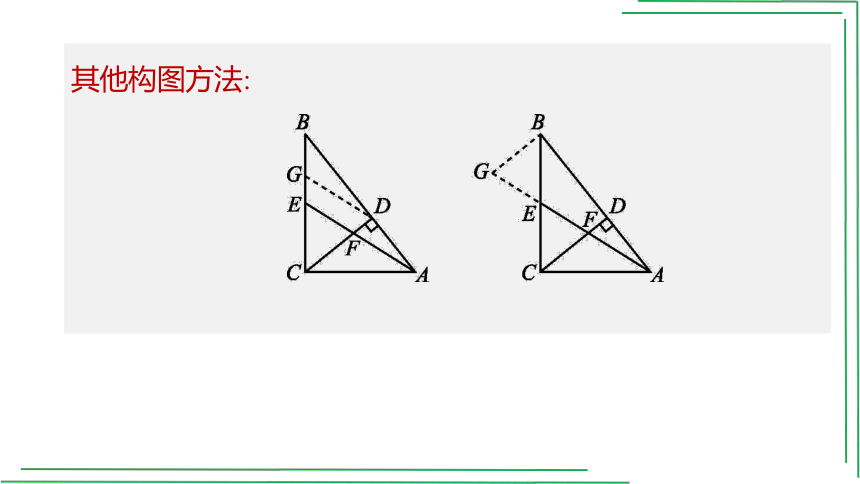
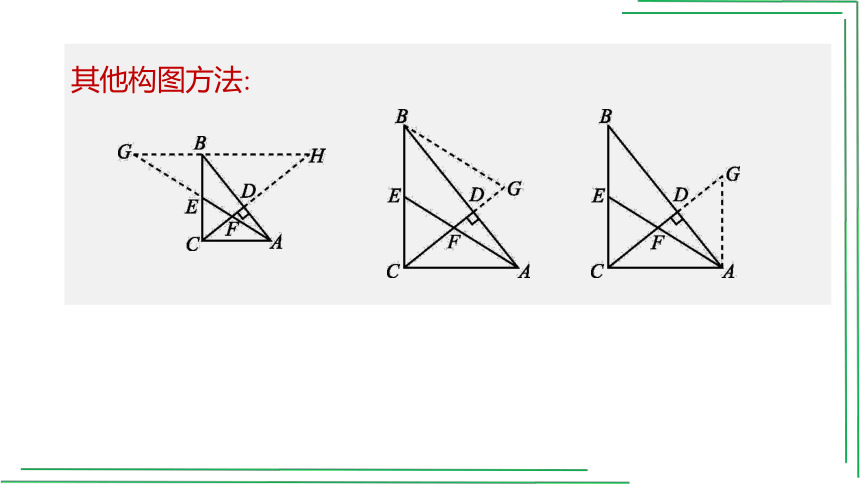
其他构图方法:
构造X型
方法二:由方法一知:CD=,AD=,BD=,
过点E作EG∥AB交CD于点G,
由平行线分线段成比例,得DG=CD=,EG=,
由EG∥AB,知△ADF∽△EGF,
∴,即,解得DF=.
其他构图方法:
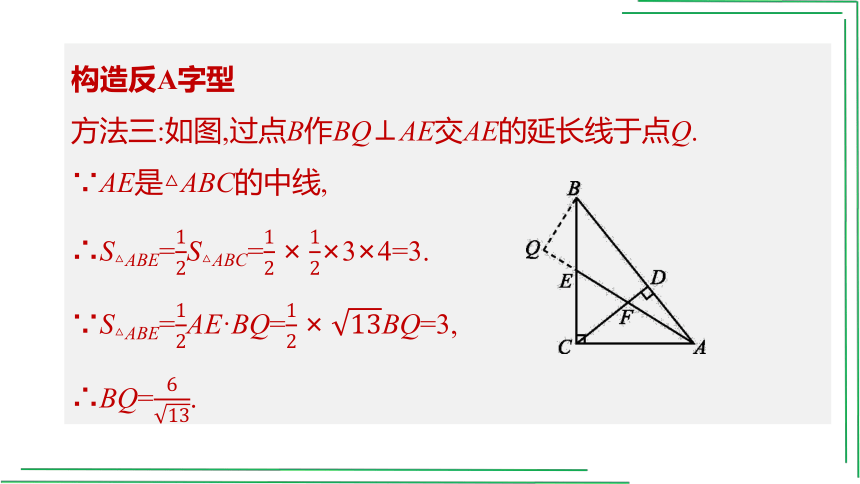
构造反A字型
方法三:如图,过点B作BQ⊥AE交AE的延长线于点Q.
∵AE是△ABC的中线,
∴S△ABE=S△ABC=×3×4=3.
∵S△ABE=AE·BQ=BQ=3,
∴BQ=.
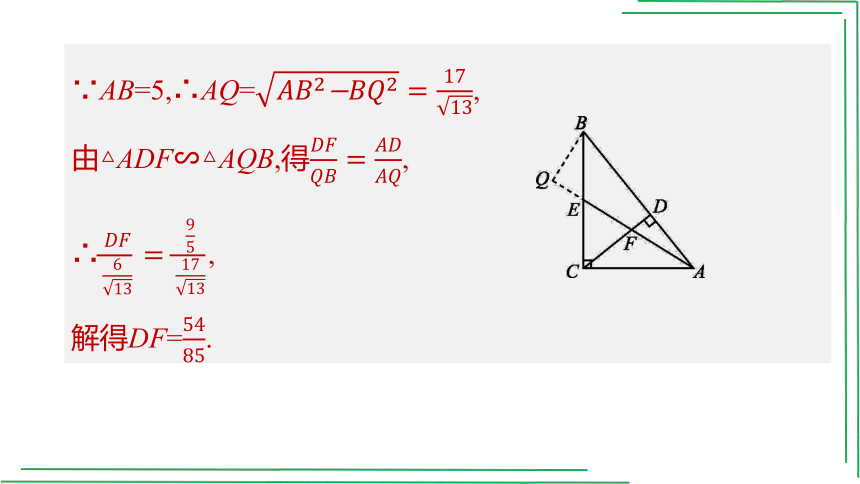
∵AB=5,∴AQ=,
由△ADF∽△AQB,得,
∴,
解得DF=.
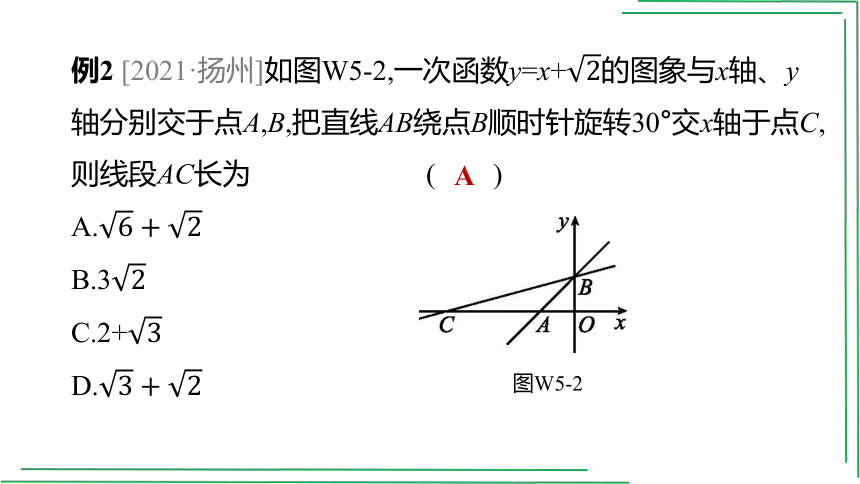
例2 [2021·扬州]如图W5-2,一次函数y=x+的图象与x轴、y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为 ( )
A.
B.3
C.2+
D.
图W5-2
A
[解析]方法一:构造子母型相似.
如图,作∠OBD=60°,交x轴于点D.
易求OD=.易得△BCA∽△DCB,
∴BC2=CA·CD.
设AC=x,
有(x+)2+()2=x(x+),
∴x=.
方法二:构造一线三垂直.
作CD⊥AB交BA延长线于D,过点D作EF∥x轴交y轴于F,作CE⊥EF于E,
易知△CED∽△DFB.
设CE=DE=a,
则DF=BF=a,BF-CE=OB=,
∴a-a=,∴a=,
∵AC=OC-AO,
∴AC=a+a-=(+1)·.
此题也可在Rt△ADC和Rt△BCD中
根据特殊角的三角函数求解,同学
们可自己尝试解决.
方法三:构造一线三等角.
作∠ECO=∠DAO=60°,与y轴分别交于点E,D.
易知△CEB∽△BDA,∴,∴BE·BD=CE·AD.
设AC=x,
则EO=x,CE=2x+2,OD=,AD=2,
∴()(x)=2(2x+2),
∴x=.
方法四:构造倍半角.
作∠CBA的平分线BD,交x轴于点D.
易知OB=OA=,OD=,BD=CD=2.
∴AD=.∴AC=+2.
方法五:构造辅助圆.
在x轴上方,以AC为边构造等边三角形MAC,作MH⊥AC,垂足为H,连接MB,
易知C,A,B三点共圆,MA=MB=MC.
设AC=2x,则AH=x,MH=x,∴M(--x,x).
∵A(-,0),B(0,),MA2=MB2,
∴(+x)2+(x-)2=x2+(x)2,∴x=,∴AC=2x=.
[方法总结]
方法一:构造“子母”型相似;方法二:构造“一线三垂直”图形;方法三:构造“一线三等角”图形;方法四:构造“倍半角”模型;方法五:构造辅助圆.
1.如图W5-3,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,
AD=1,AC=2,△ADC的面积为1,则△BCD的面积为 ( )
A.1 B.2 C.3 D.4
图W5-3
巩固训练
C
[解析]∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,∴=()2=.
∵S△ACD=1,
∴S△ABC=4,S△BCD=S△ABC-S△ACD=3.
2.如图W5-4,已知∠ACB=90°,CD⊥AB于点D,AD=4,BD=9,则CD的长为 ( )
A.2 B. C.3 D.6
图W5-4
D
[解析]易知△ADC∽△CDB,
∴CD2=AD·BD,
∴CD=6.故选D.
3.[2021·连云港]如图W5-5,△ABC中,BD⊥AB,BD,AC相交于点D,AD=AC,AB=2,∠ABC=150°,则△DBC的面积是 ( )
A. B. C. D.
图W5-5
A
[解析]如图,过点C作BD的垂线,交BD的延长线于点E,
则∠E=90°,
∵BD⊥AB,CE⊥BD,∴AB∥CE,∠ABD=90°,
∴△ABD∽△CED,∴,
∵AD=AC,∴,
∴,则CE=,
∵∠ABC=150°,∠ABD=90°,
∴∠CBE=60°,
∴BE=CE=,
∴BD=BE=,
∴S△BCD=BD·CE=.
4.如图W5-6,在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数y=(k>0,
x>0)的图象经过点B,则k的值为 ( )
A. B.8
C.10 D.
图W5-6
D
[解析]作矩形ABCD的外接矩形EFGH,
易证△DHA≌△BFC.
∵AD=5,DH=3,∴AH=4.
∴CF=OE=4.
∵OH=2,∴AO=2,∴AE=2.
易证△DHA∽△AEB,
∴,∴BE=.∴k=OE·BE=4×.
5.如图W5-7,在 ABCD中,点E在DA的延长线上,且AE=AD,连接CE交BD于点F,则的值是 .
图W5-7
[解析]∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
设AD=3a,则AE=a,
∵DE∥BC,∴△EDF∽△CBF,
∴.故答案为.
6.[2020·杭州]如图W5-8是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= ,BE= .
图W5-8
2
-1
[解析]设BE=x,则AB=AE+BE=2+x.
∵四边形ABCD是矩形,∴CD=AB=2+x,AB∥CD,∴∠DCE=∠BEC.
由折叠得∠BEC=∠DEC,EF=BE=x,
∴∠DCE=∠DEC,∴DE=CD=2+x.
∵点D,F,E在同一条直线上,∴DF=DE-EF=2+x-x=2.
∵AB∥CD,∴△DCF∽△EAF,∴,∴,
解得x1=-1,x2=--1.经检验,x1=-1,x2=--1都是分式方程的根.
∵x>0,∴x=-1,即BE=-1.
7.[2019·乐山改编]如图W5-9,在边长为的菱形ABCD中,
∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G,则CG的长为 .
图W5-9
-1
[解析]在Rt△ABE中,∠B=30°,AB=,
∴BE=.
根据折叠性质可得BF=2BE=3.
∴CF=3-.
∵AD∥CF,∴△ADG∽△FCG.
∴.设CG=x,则,解得x=-1.
8.[2019·苏州]如图W5-10,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB,过点D作DE⊥AD,交AC于点E.若DE=1,则△ABC的面积为 .
图W5-10
4
[解析]∵AB⊥AD,AD⊥DE,
∴∠BAD=∠ADE=90°,∴DE∥AB,∴∠CED=∠CAB,
∵∠C=∠C,∴△CED∽△CAB,
∵DE=1,AB=2,即DE∶AB=1∶2,
∴S△DEC∶S△ACB=1∶4,
∴S四边形ABDE∶S△ACB=3∶4.
∵S四边形ABDE=S△ABD+S△ADE=×2×2+×2×1=2+1=3,∴S△ACB=4.
9.如图W5-11,在正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°,若AB=12,AE=3,CF=4,则CG的长为 .
图W5-11
[解析]∵四边形ABCD是正方形,
∴∠B=∠C=90°,∴∠BEF+∠BFE=90°,
∵∠EFG=90°,∴∠EFB+∠GFC=90°,
∴∠BEF=∠GFC,∴△BEF∽△CFG,
∴,∴,∴CG=.
10.[2016·武汉]如图W5-12,在四边形ABCD中,∠ABC=90°,
AB=3,BC=4,CD=10,DA=5,则BD的长为 .
图W5-12
2
[解析]连接AC,过点D作DE⊥BC交BC的延长线于点E.
∵∠ABC=90°,AB=3,BC=4,∴AC=5.
∵CD=10,DA=5,AC2+CD2=AD2,∴∠ACD=90°.
又∠E=90°,易证△ABC∽△CED,
∴,即,
∴CE=6,DE=8,
∴BE=10,在Rt△BDE中,BD==2.
11.[2018·无锡改编]如图W5-13,四边形ABCD内接于☉O,AB=
17,CD=10,∠A=90°,cosB=,则AD的长为 .
图W5-13
6
[解析]方法一:如图,作矩形ABEF.
易知cos∠CDF=cos∠ABC=.
∵CD=10,∴DF=6,CF=8.
∵AB=17,∴CE=9.
易证△DFC∽△CEB,∴,即,
∴BE=12.∴AD=6.
方法二:如图,延长AD,BC交于点E,
∵AB=17,cosB=,∴EB=,AE=,
易知△EDC∽△EBA,
∴.∴ED=.∴AD=6.
12.[2020·宜宾]如图W5-14,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE平分∠ABC交AC于点E,连接CD交BE于点O.若AC=8,
BC=6,则OE的长是 .
图W5-14
[解析]方法一:作BF∥AC,交CD延长线于F,作EH⊥AB于点H,
显然EH=EC.
∵S△BCE+S△ABE=S△ABC,∴10EH+6EC=6×8,
∴EH=EC=3,∴BE=3,
易得△ADC≌△BDF,∴BF=AC=8,
易证△EOC∽△BOF,∴,∴OB=BE,
∴,∴EO=,∴EO=.
方法二:作EF∥AB,交CD于F,作EH⊥AB于H,显然EH=EC.
∵S△BCE+S△ABE=S△ABC,∴10EH+6EC=6×8,
∴EH=EC=3,∴BE=3.
易证△ECF∽△ACD,
∵,∴EF=.
易证△EOF∽△BOD,∴,
∴EO=,∴EO=.
方法三:作DF∥AC,交BE于F,作EH⊥AB于H.显然EH=EC,
∵S△BCE+S△ABE=S△ABC,∴10EH+6EC=6×8,
∴EH=EC=3,∴AE=5,BE=3,
易知DF=,易证△EOC∽△FOD,
∴,∴.
∵EF=BF,∴,∴EO=.
13.[2021·宿迁]如图W5-15,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是 .
图W5-15
[解析]连接DE.
∵CD=2BD,CE=2AE,
∴,
∵∠C=∠C,∴△CDE∽△CBA,
∴,DE∥AB,∴,
∴S△AEF=S△ABE=S△ABD,
∵BD=BC=,
∴当AB⊥BD时,△ABD的面积最大,
最大值=×4=,
∴△AEF的面积的最大值=,
故答案为.
14.[2020·长沙]如图W5-16,点P在以MN为直径的半圆上运动(点P不与M,N重合),PQ⊥MN,NE平分∠MNP,交PM于点E,交PQ于点F.
(1)= .
(2)若PN2=PM·MN,则= .
图W5-16
1
[解析](1)如图,作EH⊥MN于H,连接HF,由MN是直径,NE平分∠MNP,PQ⊥MN,易证出PE=EH=HF=PF,EH∥PQ,
∴△EMH∽△PMQ,∴,∴=1;
(2)易得△MPN∽△PQN,∴PN2=QN·MN.又∵PN2=PM·MN,
∴QN=PM,设QN=PM=a,MQ=b,由△MPQ∽△MNP得PM2=MQ·MN,∴a2=b(a+b),
解得b=或b=(舍去),
∴.
15.如图W5-17,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,求PD的值.
图W5-17
解:设PD为x,则PC=7-x,
易证∠D=∠C,
∴当时,△DAP∽△CBP,
即,解得x=;
当时,△DAP∽△CPB,
即,
解得x1=,x2=.
∴PD的长为或或.
16.[2021·广东]如图W5-18,边长为1的正方形ABCD中,点E为AD的中点.连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
解:方法一:延长BF交CD于H,连接EH.
图W5-18
∵四边形ABCD是正方形,
∴AB∥CD,∠D=∠DAB=90°,AD=CD=AB=1,
∴AC=,
由翻折的性质可知,AE=EF,∠EAB=∠EFB=90°,
∠AEB=∠FEB,
∵点E是AD的中点,
∴AE=DE=EF,
在Rt△EHD和Rt△EHF中,
∴Rt△EHD≌Rt△EHF(HL),
∴∠DEH=∠FEH,∴∠HEB=90°,
∴∠DEH+∠AEB=90°,
∵∠AEB+∠ABE=90°,
∴∠DEH=∠ABE,
∴△EDH∽△BAE,
∴,
∴DH=,CH=,
∵CH∥AB,
∴,
∴CG=AC=.
方法二:过点F作MN∥AB交AD,BC于M,N,作GH⊥BC,垂足为H.
易证△EMF∽△FNB,
设ME=a,MF=b,则FN=2a,NB=2b.
∴b+2a=1,2b-a=.解得.
∴tan∠GBC=.
设GH=3m,则CH=3m,BH=4m,BC=CH+BH=7m=1.∴m=.
∵CG=3m,∴CG=.
17.如图W5-19,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当E移动到BC的中点处时,
求证:FE平分∠DFC.
图W5-19
(1)求证:△BDE∽△CEF;
图W5-19
证明:(1)∵AB=AC,∴∠B=∠C.
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE,
且∠DEF=∠B,
∴∠BDE=∠CEF.
∴△BDE∽△CEF.
(2)当E移动到BC的中点处时,求证:FE平分∠DFC.
图W5-19
(2)∵△BDE∽△CEF,∴.
∵E是BC的中点,∴BE=CE,
∴,∴,
∵∠C=∠B=∠DEF,
∴△ECF∽△DEF,
∴∠CFE=∠EFD,∴FE平分∠DFC.
18.[2021·上海改编]如图W5-20,在四边形ABCD中,AD∥BC,
∠ABC=90°,AD=CD,O是对角线AC的中点,连接BO并延长交边CD于点E.若DE=2,OE=3,求CD的长.
图W5-20
解:延长BE,交AD延长线于F.
∵AD=CD,∴∠DAC=∠DCA.
∵AD∥BC,∴∠DAC=∠ACB,∠F=∠OBC,
∵∠ABC=90°,O是对角线AC的中点,
∴OB=OC,∴∠ACB=∠OBC,
∴∠F=∠DCA.
∵∠DEF=∠OEC,
∴△DEF∽△OEC,
∴.
设EF=2a,则CE=3a.
易证△AOF≌△COB,∴OF=OB,∴EB=6+2a.
易证△DEF∽△CEB,
∴,∴,∴3a2-2a-6=0,
∴a=或(舍去),
∴CD=3+.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
提分微课 05
相似模型的应用
●构图模型
●例题精析
●巩固训练
“相似”是求线段长和线段比值的重要工具之一,因此,同学们要注意掌握相似的基本图形及其各种演变和联系.
例1 [2020·山西]如图W5-1,在Rt△ABC中,∠ACB=90°,AC=3,
BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为 .
图W5-1
[思路分析]
此题易求CD的值,因此可转化为求CF,FD与CD的比例关系.
根据平行线构造A字型或X型或构造反A字型等相似图形.从而求得比例关系.
[解析]构造A字型
方法一:已知∠ACB=90°,AC=3,BC=4,由勾股定理,得AB=5.
∵CD⊥AB,
∴AB·CD=AC·BC,∴CD=.
如图,过点E作EH⊥AB于点H.则EH∥CD,
∴△BEH∽△BCD,
∴,∴EH=CD=.
易得△ABC∽△ACD,
∴,得AD=,
由△ABC∽△CBD,得,
∴BD=.∴DH=BD=.
由△ADF∽△AHE,得,∴,解得DF=.
其他构图方法:
构造X型
方法二:由方法一知:CD=,AD=,BD=,
过点E作EG∥AB交CD于点G,
由平行线分线段成比例,得DG=CD=,EG=,
由EG∥AB,知△ADF∽△EGF,
∴,即,解得DF=.
其他构图方法:
构造反A字型
方法三:如图,过点B作BQ⊥AE交AE的延长线于点Q.
∵AE是△ABC的中线,
∴S△ABE=S△ABC=×3×4=3.
∵S△ABE=AE·BQ=BQ=3,
∴BQ=.
∵AB=5,∴AQ=,
由△ADF∽△AQB,得,
∴,
解得DF=.
例2 [2021·扬州]如图W5-2,一次函数y=x+的图象与x轴、y轴分别交于点A,B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为 ( )
A.
B.3
C.2+
D.
图W5-2
A
[解析]方法一:构造子母型相似.
如图,作∠OBD=60°,交x轴于点D.
易求OD=.易得△BCA∽△DCB,
∴BC2=CA·CD.
设AC=x,
有(x+)2+()2=x(x+),
∴x=.
方法二:构造一线三垂直.
作CD⊥AB交BA延长线于D,过点D作EF∥x轴交y轴于F,作CE⊥EF于E,
易知△CED∽△DFB.
设CE=DE=a,
则DF=BF=a,BF-CE=OB=,
∴a-a=,∴a=,
∵AC=OC-AO,
∴AC=a+a-=(+1)·.
此题也可在Rt△ADC和Rt△BCD中
根据特殊角的三角函数求解,同学
们可自己尝试解决.
方法三:构造一线三等角.
作∠ECO=∠DAO=60°,与y轴分别交于点E,D.
易知△CEB∽△BDA,∴,∴BE·BD=CE·AD.
设AC=x,
则EO=x,CE=2x+2,OD=,AD=2,
∴()(x)=2(2x+2),
∴x=.
方法四:构造倍半角.
作∠CBA的平分线BD,交x轴于点D.
易知OB=OA=,OD=,BD=CD=2.
∴AD=.∴AC=+2.
方法五:构造辅助圆.
在x轴上方,以AC为边构造等边三角形MAC,作MH⊥AC,垂足为H,连接MB,
易知C,A,B三点共圆,MA=MB=MC.
设AC=2x,则AH=x,MH=x,∴M(--x,x).
∵A(-,0),B(0,),MA2=MB2,
∴(+x)2+(x-)2=x2+(x)2,∴x=,∴AC=2x=.
[方法总结]
方法一:构造“子母”型相似;方法二:构造“一线三垂直”图形;方法三:构造“一线三等角”图形;方法四:构造“倍半角”模型;方法五:构造辅助圆.
1.如图W5-3,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,
AD=1,AC=2,△ADC的面积为1,则△BCD的面积为 ( )
A.1 B.2 C.3 D.4
图W5-3
巩固训练
C
[解析]∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,∴=()2=.
∵S△ACD=1,
∴S△ABC=4,S△BCD=S△ABC-S△ACD=3.
2.如图W5-4,已知∠ACB=90°,CD⊥AB于点D,AD=4,BD=9,则CD的长为 ( )
A.2 B. C.3 D.6
图W5-4
D
[解析]易知△ADC∽△CDB,
∴CD2=AD·BD,
∴CD=6.故选D.
3.[2021·连云港]如图W5-5,△ABC中,BD⊥AB,BD,AC相交于点D,AD=AC,AB=2,∠ABC=150°,则△DBC的面积是 ( )
A. B. C. D.
图W5-5
A
[解析]如图,过点C作BD的垂线,交BD的延长线于点E,
则∠E=90°,
∵BD⊥AB,CE⊥BD,∴AB∥CE,∠ABD=90°,
∴△ABD∽△CED,∴,
∵AD=AC,∴,
∴,则CE=,
∵∠ABC=150°,∠ABD=90°,
∴∠CBE=60°,
∴BE=CE=,
∴BD=BE=,
∴S△BCD=BD·CE=.
4.如图W5-6,在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数y=(k>0,
x>0)的图象经过点B,则k的值为 ( )
A. B.8
C.10 D.
图W5-6
D
[解析]作矩形ABCD的外接矩形EFGH,
易证△DHA≌△BFC.
∵AD=5,DH=3,∴AH=4.
∴CF=OE=4.
∵OH=2,∴AO=2,∴AE=2.
易证△DHA∽△AEB,
∴,∴BE=.∴k=OE·BE=4×.
5.如图W5-7,在 ABCD中,点E在DA的延长线上,且AE=AD,连接CE交BD于点F,则的值是 .
图W5-7
[解析]∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
设AD=3a,则AE=a,
∵DE∥BC,∴△EDF∽△CBF,
∴.故答案为.
6.[2020·杭州]如图W5-8是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= ,BE= .
图W5-8
2
-1
[解析]设BE=x,则AB=AE+BE=2+x.
∵四边形ABCD是矩形,∴CD=AB=2+x,AB∥CD,∴∠DCE=∠BEC.
由折叠得∠BEC=∠DEC,EF=BE=x,
∴∠DCE=∠DEC,∴DE=CD=2+x.
∵点D,F,E在同一条直线上,∴DF=DE-EF=2+x-x=2.
∵AB∥CD,∴△DCF∽△EAF,∴,∴,
解得x1=-1,x2=--1.经检验,x1=-1,x2=--1都是分式方程的根.
∵x>0,∴x=-1,即BE=-1.
7.[2019·乐山改编]如图W5-9,在边长为的菱形ABCD中,
∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G,则CG的长为 .
图W5-9
-1
[解析]在Rt△ABE中,∠B=30°,AB=,
∴BE=.
根据折叠性质可得BF=2BE=3.
∴CF=3-.
∵AD∥CF,∴△ADG∽△FCG.
∴.设CG=x,则,解得x=-1.
8.[2019·苏州]如图W5-10,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB,过点D作DE⊥AD,交AC于点E.若DE=1,则△ABC的面积为 .
图W5-10
4
[解析]∵AB⊥AD,AD⊥DE,
∴∠BAD=∠ADE=90°,∴DE∥AB,∴∠CED=∠CAB,
∵∠C=∠C,∴△CED∽△CAB,
∵DE=1,AB=2,即DE∶AB=1∶2,
∴S△DEC∶S△ACB=1∶4,
∴S四边形ABDE∶S△ACB=3∶4.
∵S四边形ABDE=S△ABD+S△ADE=×2×2+×2×1=2+1=3,∴S△ACB=4.
9.如图W5-11,在正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°,若AB=12,AE=3,CF=4,则CG的长为 .
图W5-11
[解析]∵四边形ABCD是正方形,
∴∠B=∠C=90°,∴∠BEF+∠BFE=90°,
∵∠EFG=90°,∴∠EFB+∠GFC=90°,
∴∠BEF=∠GFC,∴△BEF∽△CFG,
∴,∴,∴CG=.
10.[2016·武汉]如图W5-12,在四边形ABCD中,∠ABC=90°,
AB=3,BC=4,CD=10,DA=5,则BD的长为 .
图W5-12
2
[解析]连接AC,过点D作DE⊥BC交BC的延长线于点E.
∵∠ABC=90°,AB=3,BC=4,∴AC=5.
∵CD=10,DA=5,AC2+CD2=AD2,∴∠ACD=90°.
又∠E=90°,易证△ABC∽△CED,
∴,即,
∴CE=6,DE=8,
∴BE=10,在Rt△BDE中,BD==2.
11.[2018·无锡改编]如图W5-13,四边形ABCD内接于☉O,AB=
17,CD=10,∠A=90°,cosB=,则AD的长为 .
图W5-13
6
[解析]方法一:如图,作矩形ABEF.
易知cos∠CDF=cos∠ABC=.
∵CD=10,∴DF=6,CF=8.
∵AB=17,∴CE=9.
易证△DFC∽△CEB,∴,即,
∴BE=12.∴AD=6.
方法二:如图,延长AD,BC交于点E,
∵AB=17,cosB=,∴EB=,AE=,
易知△EDC∽△EBA,
∴.∴ED=.∴AD=6.
12.[2020·宜宾]如图W5-14,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE平分∠ABC交AC于点E,连接CD交BE于点O.若AC=8,
BC=6,则OE的长是 .
图W5-14
[解析]方法一:作BF∥AC,交CD延长线于F,作EH⊥AB于点H,
显然EH=EC.
∵S△BCE+S△ABE=S△ABC,∴10EH+6EC=6×8,
∴EH=EC=3,∴BE=3,
易得△ADC≌△BDF,∴BF=AC=8,
易证△EOC∽△BOF,∴,∴OB=BE,
∴,∴EO=,∴EO=.
方法二:作EF∥AB,交CD于F,作EH⊥AB于H,显然EH=EC.
∵S△BCE+S△ABE=S△ABC,∴10EH+6EC=6×8,
∴EH=EC=3,∴BE=3.
易证△ECF∽△ACD,
∵,∴EF=.
易证△EOF∽△BOD,∴,
∴EO=,∴EO=.
方法三:作DF∥AC,交BE于F,作EH⊥AB于H.显然EH=EC,
∵S△BCE+S△ABE=S△ABC,∴10EH+6EC=6×8,
∴EH=EC=3,∴AE=5,BE=3,
易知DF=,易证△EOC∽△FOD,
∴,∴.
∵EF=BF,∴,∴EO=.
13.[2021·宿迁]如图W5-15,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是 .
图W5-15
[解析]连接DE.
∵CD=2BD,CE=2AE,
∴,
∵∠C=∠C,∴△CDE∽△CBA,
∴,DE∥AB,∴,
∴S△AEF=S△ABE=S△ABD,
∵BD=BC=,
∴当AB⊥BD时,△ABD的面积最大,
最大值=×4=,
∴△AEF的面积的最大值=,
故答案为.
14.[2020·长沙]如图W5-16,点P在以MN为直径的半圆上运动(点P不与M,N重合),PQ⊥MN,NE平分∠MNP,交PM于点E,交PQ于点F.
(1)= .
(2)若PN2=PM·MN,则= .
图W5-16
1
[解析](1)如图,作EH⊥MN于H,连接HF,由MN是直径,NE平分∠MNP,PQ⊥MN,易证出PE=EH=HF=PF,EH∥PQ,
∴△EMH∽△PMQ,∴,∴=1;
(2)易得△MPN∽△PQN,∴PN2=QN·MN.又∵PN2=PM·MN,
∴QN=PM,设QN=PM=a,MQ=b,由△MPQ∽△MNP得PM2=MQ·MN,∴a2=b(a+b),
解得b=或b=(舍去),
∴.
15.如图W5-17,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,求PD的值.
图W5-17
解:设PD为x,则PC=7-x,
易证∠D=∠C,
∴当时,△DAP∽△CBP,
即,解得x=;
当时,△DAP∽△CPB,
即,
解得x1=,x2=.
∴PD的长为或或.
16.[2021·广东]如图W5-18,边长为1的正方形ABCD中,点E为AD的中点.连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
解:方法一:延长BF交CD于H,连接EH.
图W5-18
∵四边形ABCD是正方形,
∴AB∥CD,∠D=∠DAB=90°,AD=CD=AB=1,
∴AC=,
由翻折的性质可知,AE=EF,∠EAB=∠EFB=90°,
∠AEB=∠FEB,
∵点E是AD的中点,
∴AE=DE=EF,
在Rt△EHD和Rt△EHF中,
∴Rt△EHD≌Rt△EHF(HL),
∴∠DEH=∠FEH,∴∠HEB=90°,
∴∠DEH+∠AEB=90°,
∵∠AEB+∠ABE=90°,
∴∠DEH=∠ABE,
∴△EDH∽△BAE,
∴,
∴DH=,CH=,
∵CH∥AB,
∴,
∴CG=AC=.
方法二:过点F作MN∥AB交AD,BC于M,N,作GH⊥BC,垂足为H.
易证△EMF∽△FNB,
设ME=a,MF=b,则FN=2a,NB=2b.
∴b+2a=1,2b-a=.解得.
∴tan∠GBC=.
设GH=3m,则CH=3m,BH=4m,BC=CH+BH=7m=1.∴m=.
∵CG=3m,∴CG=.
17.如图W5-19,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当E移动到BC的中点处时,
求证:FE平分∠DFC.
图W5-19
(1)求证:△BDE∽△CEF;
图W5-19
证明:(1)∵AB=AC,∴∠B=∠C.
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE,
且∠DEF=∠B,
∴∠BDE=∠CEF.
∴△BDE∽△CEF.
(2)当E移动到BC的中点处时,求证:FE平分∠DFC.
图W5-19
(2)∵△BDE∽△CEF,∴.
∵E是BC的中点,∴BE=CE,
∴,∴,
∵∠C=∠B=∠DEF,
∴△ECF∽△DEF,
∴∠CFE=∠EFD,∴FE平分∠DFC.
18.[2021·上海改编]如图W5-20,在四边形ABCD中,AD∥BC,
∠ABC=90°,AD=CD,O是对角线AC的中点,连接BO并延长交边CD于点E.若DE=2,OE=3,求CD的长.
图W5-20
解:延长BE,交AD延长线于F.
∵AD=CD,∴∠DAC=∠DCA.
∵AD∥BC,∴∠DAC=∠ACB,∠F=∠OBC,
∵∠ABC=90°,O是对角线AC的中点,
∴OB=OC,∴∠ACB=∠OBC,
∴∠F=∠DCA.
∵∠DEF=∠OEC,
∴△DEF∽△OEC,
∴.
设EF=2a,则CE=3a.
易证△AOF≌△COB,∴OF=OB,∴EB=6+2a.
易证△DEF∽△CEB,
∴,∴,∴3a2-2a-6=0,
∴a=或(舍去),
∴CD=3+.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
