2022中考数学三轮冲刺考前提分微课07 折叠问题 课件(共31张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺考前提分微课07 折叠问题 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 11:07:33 | ||
图片预览








文档简介
(共31张PPT)
2022年中考数学三轮复习(人教版)
提分微课 07
折叠问题
●方法介绍
●例题精析
●巩固训练
近年来,折叠问题逐渐成为中考命题的高频热点,尤其是三角形、四边形的折叠问题频频现身.图形的折叠实质上是全等变换,即折叠前后的图形全等,解决这类问题时要牢牢抓住因折叠形成的等线段、等角,这些等量关系是解决此类问题的关键.这类问题的知识面涉及较为广泛,往往与勾股定理、方程、相似、函数、面积等知识融为一体,解题中我们要善于发现图形的特点,通过推理或列方程求解.
方法介绍
以常见的三角形和四边形的折叠去探究折叠问题中的“一二一”:“一个本质+二项归类+一种思想”.
一个本质——折叠问题的本质是全等变换;
二项归类——折叠问题通常用于求角度和长度;
一种思想——方程思想.
例题精析
例1 如图W7-1,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将点A折叠到点B处,则折痕DE的长度为 .
图W7-1
[解析]方法一(相似处理):
∵△ADE∽△ABC,∴,即,DE=.
方法二(勾股定理处理):设CD=x,则AD=BD=4-x,
∴x2+32=(4-x)2,x=,则BD=,
∴DE=.
方法三(面积处理):由方法二知CD=,∵S△ABC=S△ABD+S△BCD,即×3×4=×3××5×DE,∴DE=.
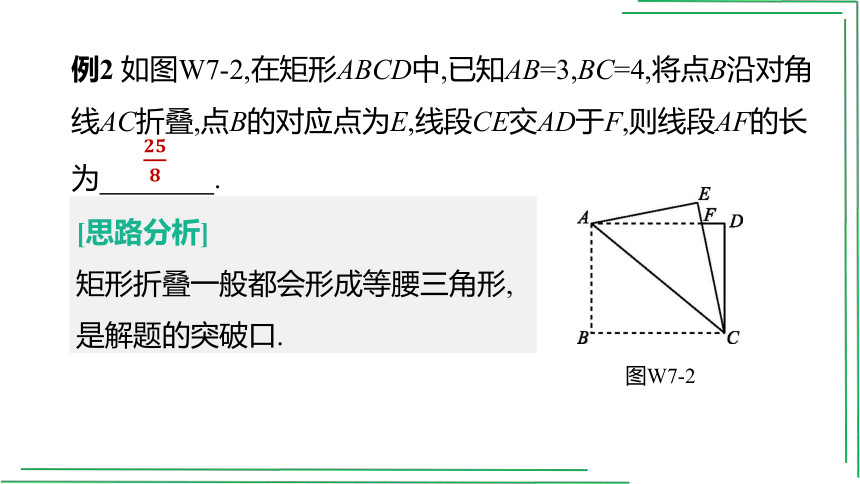
例2 如图W7-2,在矩形ABCD中,已知AB=3,BC=4,将点B沿对角线AC折叠,点B的对应点为E,线段CE交AD于F,则线段AF的长
为 .
图W7-2
[思路分析]
矩形折叠一般都会形成等腰三角形,是解题的突破口.
[解析]方法一(勾股定理法):
设AF=x,则CF=x,DF=4-x,
在Rt△DFC中,x2=(4-x)2+32,解得x=.
方法二(相似处理)(三角函数处理):
作FG⊥AC于G,则AG=,则AF=,
即AF=.∴AF=.
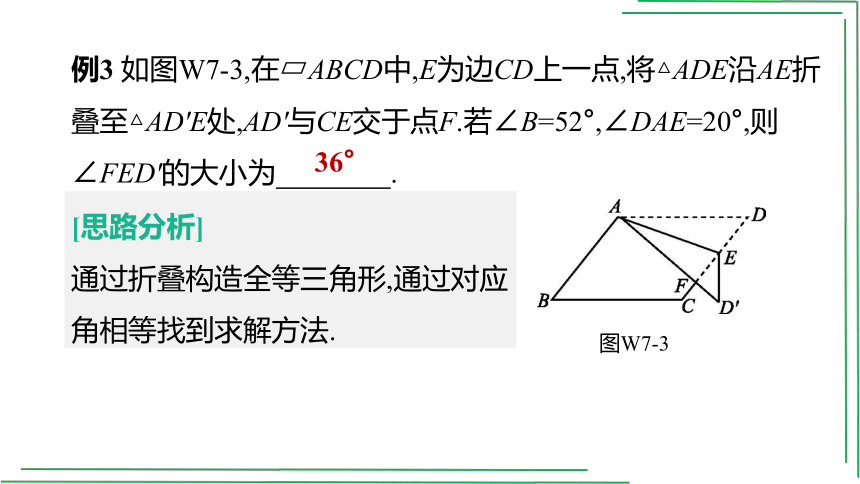
例3 如图W7-3,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED'的大小为 .
图W7-3
[思路分析]
通过折叠构造全等三角形,通过对应角相等找到求解方法.
36°
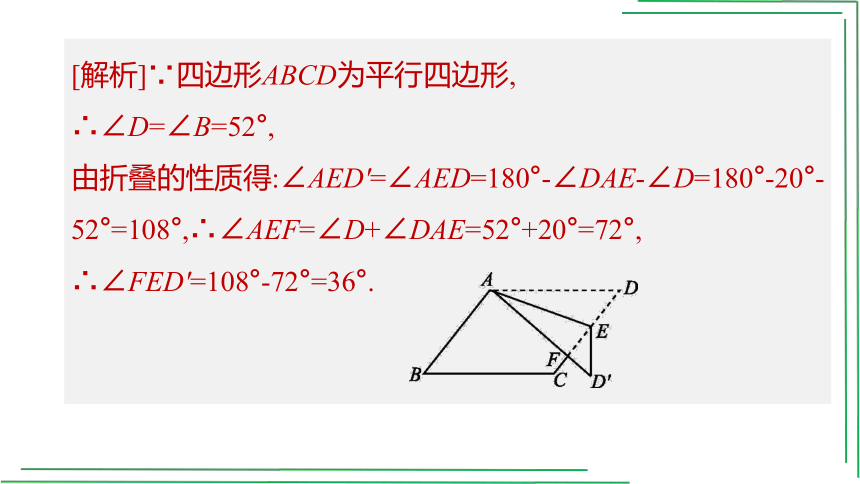
[解析]∵四边形ABCD为平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠AED'=∠AED=180°-∠DAE-∠D=180°-20°-52°=108°,∴∠AEF=∠D+∠DAE=52°+20°=72°,
∴∠FED'=108°-72°=36°.
例4 如图W7-4,在矩形ABCD中,AD=2,AB=3,点E是AD边的中点,点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A'EF,连接A'C,则A'C的最小值为 .
图W7-4
[思路分析]
如果翻折的折痕是过一定点的,就会出现隐形圆,一般我们用点圆最值模型来求最值.
-1
[解析]根据点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A'EF,可得点A'的运动路径为以E为圆心,AE长为半径的半圆,再根据两点之间线段最短,即可得出当点A',C,E三点共线时,A'C的长最小,
因为EC=,
所以A'C的最小值为-1.
巩固训练
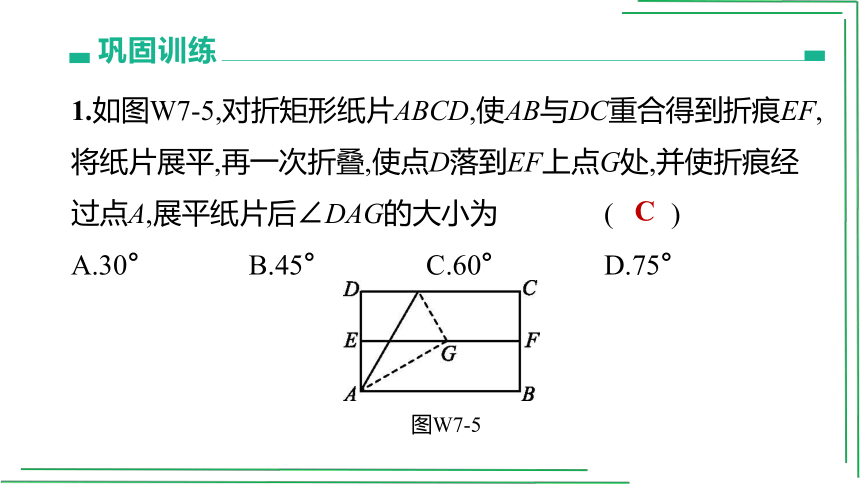
1.如图W7-5,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 ( )
A.30° B.45° C.60° D.75°
图W7-5
C
2.如图W7-6,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为 ( )
A.66° B.104° C.114° D.124°
图W7-6
C
3.如图W7-7①,四边形ABCD是一矩形纸片,AB=6 cm,AD=8 cm,E是AD上一点,且AE=6 cm.操作:(1)将AB向AE折过去,使AB与AE重合,得折痕AF,如图②;(2)将△AFB以BF为折痕向右折过去,得图③.则△GFC的面积是( )
A.1 cm2
B.2 cm2
C.3 cm2
D.4 cm2
图W7-7
B
4.如图W7-8,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4 C.5 D.6
图W7-8
B
[解析]由题意设CH=x,则DH=EH=9-x,
∵BE∶EC=2∶1,∴CE=BC=3,
在Rt△ECH中,EH2=EC2+CH2,
即(9-x)2=32+x2,解得x=4,即CH=4.
5.[2019·邵阳]如图W7-9,在Rt△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于 ( )
A.120° B.108° C.72° D.36°
图W7-9
B
6.如图W7-10,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将点C折叠到点E处,折痕为BD,则DE的长度为 .
图W7-10
[解析]方法一(勾股定理处理):由对称性可设DE=DC=x,则AD=4-x,
∴在Rt△ADE中,x2+22=(4-x)2,则x=.
方法二(面积处理):∵S△ABC=S△ABD+S△BCD,
即×3×4=×3×DE+×5×DE,∴DE=.
方法三(相似处理):设DE=x,则AD=4-x,
∵△ADE∽△ABC,∴,
即,∴x=,∴DE=.
7.如图W7-11,在矩形纸片ABCD中,AD=4 cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5 cm,则AB的长为
.
图W7-11
8 cm
[解析]根据折叠前后对应角相等可知∠BAC=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∴∠BAC=∠ACD,
∴∠EAC=∠ACD,∴AO=CO=5 cm.
在直角三角形ADO中,DO==3(cm),
∴AB=CD=DO+CO=3+5=8 (cm).
8.如图W7-12,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将点A折叠到点A'处,使四边形ADA'E为菱形,则折痕DE的长度为 .
图W7-12
9.[2019·淮安]如图W7-13,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连接AP,则tan∠HAP= .
图W7-13
[解析]如图所示,连接PB交CH于点O.
∵H是AB的中点,∴HB=AB=.
∵将△CBH沿CH折叠,点B落在矩形内点P处,
∴HP=HB,PB=2BO=2×=2×=2×.
∵HP=HB=AB,∴△APB是直角三角形,∴tan∠HAP=.
10.如图W7-14,在边长为8的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一点.将△AMN沿MN所在的直线翻折得到△A'MN,连接A'B,则A'B的取值范围为 .
图W7-14
4-4≤A'B≤8
[解析]连接BM,BD.
∵M是边AD的中点,△AMN沿MN所在的直线翻折得到△A'MN,
∴点A'的轨迹为以AD为直径的半圆M,A'M=AM=4.
∵∠A=60°,AB=AD,
∴△ABD是等边三角形,
∴BM⊥AD,∠ABM=30°,∴BM=AM=4.
∵A'B+A'M≥BM,∴A'B≥BM-A'M=4-4.
当点N与点A或点D重合时,点A'与点A或点D重合,此时A'B的最大值为8,
∴A'B的取值范围为4-4≤A'B≤8.
故答案为4-4≤A'B≤8.
11.如图W7-15,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E,F分别为AB,AC上一个动点,连接EF,以EF为轴将△AEF折叠得到△DEF,使点D落在BC上,当△BDE为直角三角形时,BE的值为多少
图W7-15
解:如图①,当∠BDE=90°时,设BE=x,
则AE=DE=10-x,
∵DE∥AC,∴,∴,∴x=.
如图②,当∠DEB=90°时,设BE=x,
则AE=ED=10-x,
∵tan∠DBE=,∴,∴x=,
综上所述,满足条件的BE的值为或.
https://www.21cnjy.com/help/help_extract.php
2022年中考数学三轮复习(人教版)
提分微课 07
折叠问题
●方法介绍
●例题精析
●巩固训练
近年来,折叠问题逐渐成为中考命题的高频热点,尤其是三角形、四边形的折叠问题频频现身.图形的折叠实质上是全等变换,即折叠前后的图形全等,解决这类问题时要牢牢抓住因折叠形成的等线段、等角,这些等量关系是解决此类问题的关键.这类问题的知识面涉及较为广泛,往往与勾股定理、方程、相似、函数、面积等知识融为一体,解题中我们要善于发现图形的特点,通过推理或列方程求解.
方法介绍
以常见的三角形和四边形的折叠去探究折叠问题中的“一二一”:“一个本质+二项归类+一种思想”.
一个本质——折叠问题的本质是全等变换;
二项归类——折叠问题通常用于求角度和长度;
一种思想——方程思想.
例题精析
例1 如图W7-1,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将点A折叠到点B处,则折痕DE的长度为 .
图W7-1
[解析]方法一(相似处理):
∵△ADE∽△ABC,∴,即,DE=.
方法二(勾股定理处理):设CD=x,则AD=BD=4-x,
∴x2+32=(4-x)2,x=,则BD=,
∴DE=.
方法三(面积处理):由方法二知CD=,∵S△ABC=S△ABD+S△BCD,即×3×4=×3××5×DE,∴DE=.
例2 如图W7-2,在矩形ABCD中,已知AB=3,BC=4,将点B沿对角线AC折叠,点B的对应点为E,线段CE交AD于F,则线段AF的长
为 .
图W7-2
[思路分析]
矩形折叠一般都会形成等腰三角形,是解题的突破口.
[解析]方法一(勾股定理法):
设AF=x,则CF=x,DF=4-x,
在Rt△DFC中,x2=(4-x)2+32,解得x=.
方法二(相似处理)(三角函数处理):
作FG⊥AC于G,则AG=,则AF=,
即AF=.∴AF=.
例3 如图W7-3,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED'的大小为 .
图W7-3
[思路分析]
通过折叠构造全等三角形,通过对应角相等找到求解方法.
36°
[解析]∵四边形ABCD为平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠AED'=∠AED=180°-∠DAE-∠D=180°-20°-52°=108°,∴∠AEF=∠D+∠DAE=52°+20°=72°,
∴∠FED'=108°-72°=36°.
例4 如图W7-4,在矩形ABCD中,AD=2,AB=3,点E是AD边的中点,点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A'EF,连接A'C,则A'C的最小值为 .
图W7-4
[思路分析]
如果翻折的折痕是过一定点的,就会出现隐形圆,一般我们用点圆最值模型来求最值.
-1
[解析]根据点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A'EF,可得点A'的运动路径为以E为圆心,AE长为半径的半圆,再根据两点之间线段最短,即可得出当点A',C,E三点共线时,A'C的长最小,
因为EC=,
所以A'C的最小值为-1.
巩固训练
1.如图W7-5,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 ( )
A.30° B.45° C.60° D.75°
图W7-5
C
2.如图W7-6,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为 ( )
A.66° B.104° C.114° D.124°
图W7-6
C
3.如图W7-7①,四边形ABCD是一矩形纸片,AB=6 cm,AD=8 cm,E是AD上一点,且AE=6 cm.操作:(1)将AB向AE折过去,使AB与AE重合,得折痕AF,如图②;(2)将△AFB以BF为折痕向右折过去,得图③.则△GFC的面积是( )
A.1 cm2
B.2 cm2
C.3 cm2
D.4 cm2
图W7-7
B
4.如图W7-8,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4 C.5 D.6
图W7-8
B
[解析]由题意设CH=x,则DH=EH=9-x,
∵BE∶EC=2∶1,∴CE=BC=3,
在Rt△ECH中,EH2=EC2+CH2,
即(9-x)2=32+x2,解得x=4,即CH=4.
5.[2019·邵阳]如图W7-9,在Rt△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于 ( )
A.120° B.108° C.72° D.36°
图W7-9
B
6.如图W7-10,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将点C折叠到点E处,折痕为BD,则DE的长度为 .
图W7-10
[解析]方法一(勾股定理处理):由对称性可设DE=DC=x,则AD=4-x,
∴在Rt△ADE中,x2+22=(4-x)2,则x=.
方法二(面积处理):∵S△ABC=S△ABD+S△BCD,
即×3×4=×3×DE+×5×DE,∴DE=.
方法三(相似处理):设DE=x,则AD=4-x,
∵△ADE∽△ABC,∴,
即,∴x=,∴DE=.
7.如图W7-11,在矩形纸片ABCD中,AD=4 cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5 cm,则AB的长为
.
图W7-11
8 cm
[解析]根据折叠前后对应角相等可知∠BAC=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∴∠BAC=∠ACD,
∴∠EAC=∠ACD,∴AO=CO=5 cm.
在直角三角形ADO中,DO==3(cm),
∴AB=CD=DO+CO=3+5=8 (cm).
8.如图W7-12,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将点A折叠到点A'处,使四边形ADA'E为菱形,则折痕DE的长度为 .
图W7-12
9.[2019·淮安]如图W7-13,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连接AP,则tan∠HAP= .
图W7-13
[解析]如图所示,连接PB交CH于点O.
∵H是AB的中点,∴HB=AB=.
∵将△CBH沿CH折叠,点B落在矩形内点P处,
∴HP=HB,PB=2BO=2×=2×=2×.
∵HP=HB=AB,∴△APB是直角三角形,∴tan∠HAP=.
10.如图W7-14,在边长为8的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一点.将△AMN沿MN所在的直线翻折得到△A'MN,连接A'B,则A'B的取值范围为 .
图W7-14
4-4≤A'B≤8
[解析]连接BM,BD.
∵M是边AD的中点,△AMN沿MN所在的直线翻折得到△A'MN,
∴点A'的轨迹为以AD为直径的半圆M,A'M=AM=4.
∵∠A=60°,AB=AD,
∴△ABD是等边三角形,
∴BM⊥AD,∠ABM=30°,∴BM=AM=4.
∵A'B+A'M≥BM,∴A'B≥BM-A'M=4-4.
当点N与点A或点D重合时,点A'与点A或点D重合,此时A'B的最大值为8,
∴A'B的取值范围为4-4≤A'B≤8.
故答案为4-4≤A'B≤8.
11.如图W7-15,在Rt△ABC中,∠C=90°,AC=6,BC=8,点E,F分别为AB,AC上一个动点,连接EF,以EF为轴将△AEF折叠得到△DEF,使点D落在BC上,当△BDE为直角三角形时,BE的值为多少
图W7-15
解:如图①,当∠BDE=90°时,设BE=x,
则AE=DE=10-x,
∵DE∥AC,∴,∴,∴x=.
如图②,当∠DEB=90°时,设BE=x,
则AE=ED=10-x,
∵tan∠DBE=,∴,∴x=,
综上所述,满足条件的BE的值为或.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
